Right Angled Artin Groups

16 Aug 2020

I’m starting my PhD at UC Riverside this fall, and I’ve enrolled in a program that introduces me to some faculty and gets me familiar with the campus… Or, it would were it not for covid. Regardless, I’ve been meeting with a summer advisor (Matt Durham) over zoom every week for a while now to talk about hyperbolic surfaces and mapping class groups. I’m not sure I’m ready to make a blog post about that material, but last week we talked about Right Angled Artin Groups (RAAGs), which arise as subgroups of mapping class groups in a very natural way (cf. this article by Thomas Koberda). Raags, as we’ll soon see, are controlled by their combinatorial structure, which gives us a good way of creating counterexamples by converting algebraic conditions into combinatorial ones.

Let’s start getting to the meat of things: What is a raag?

That is, $A(\mathrm{\Gamma })$ is freely generated by the vertices of $\mathrm{\Gamma }$, with relations saying that two vertices commute if and only if they are joined by an edge.

⚠ Warning: Some people use the opposite convention, and say $x$ and $y$ commute whenever they aren’t joined by an edge in $\mathrm{\Gamma }$. Obviously these are equivalent, by passing to the complement graph, but it’s good to know that this ambiguity exists in the literature. Notably the sage package for raags uses the opposite convention.

Of course a definition is no good without examples, so let’s give a few concrete ones:

---

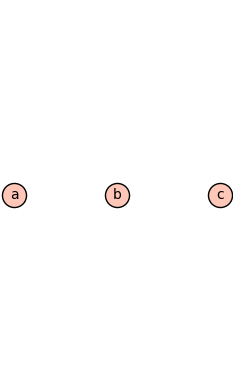
We’ll start with $\mathrm{\Gamma }=K_3$, the complete graph on $3$ vertices:

With this graph, we’ll have a generator for each vertex $a,b,c$. Moreoever, since we have an edge conecting each of them, every generator will commute with every other generator.

Then $A(K_3)=⟨a,b,c|[a,b],[a,c],[b,c]⟩$, which we recognize as ${\mathbb{Z}}^3$.

---

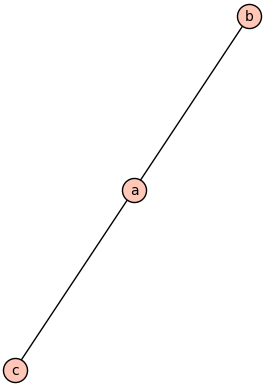
Next, let’s look at the opposite extreme. Let $D_3$ be the discrete graph:

$A(D_3)$ will still have generators $a$, $b$, and $c$. But now there are no edges, which means there will be no relations between them! Thus $A(D_3)=⟨a,b,c⟩\cong F_3$ is the free group on $3$ generators.

---

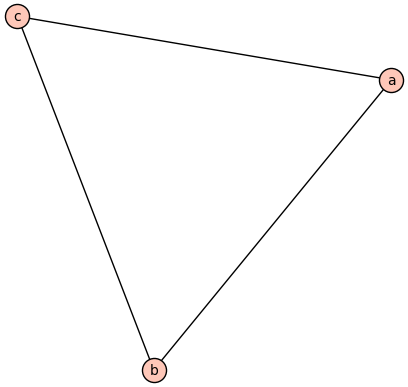
Finally, let’s look somewhere in between. Let $P_3$ be the path graph with $3$ vertices:

Then $A(P_3)$ will be $⟨a,b,c|[a,b],[a,c]⟩$. Here $a$ commutes with $b$ and $c$, since $a$ is adjacent to both of them. However, $b$ and $c$ don’t commute, since they are not adjacent. Notice it’s already less clear if there’s a simple description of this group, unlike the previous two examples. This is a big part of the power of raags: they let us build complicated groups in a way that we can still understand. The trick is to think combinatorially instead of algebraically.

As an aside, this is not unlike the automata groups that I worked with in my undergraduate thesis. In that setting we leveraged the combinatorics of Mealy Automata in order to understand complicated groups of automorphisms of the infinite binary tree. Automata groups are also rich sources of counterexamples (cf. the grigorchuk group) in group theory for the same reason as raags. In fact, automata groups are so complicated that we still haven’t classified all the groups you can get from an automaton with only $3$ states! That said, a lot of work has been done.

---

Coming back to raags, it is easy to see that $A(D_n)\cong F_n$ and $A(K_n)\cong {\mathbb{Z}}^n$ for every $n$. Then adding edges interpolates between free groups and free abelian groups in a way that we can control. This is not unlike the way the Lovasz Local Lemma interpolates between a product bound and a union bound based on the dependency graph of random variables.

As a quick exercise, what is $A(\mathrm{\Gamma })$ for the square graph shown below?

---

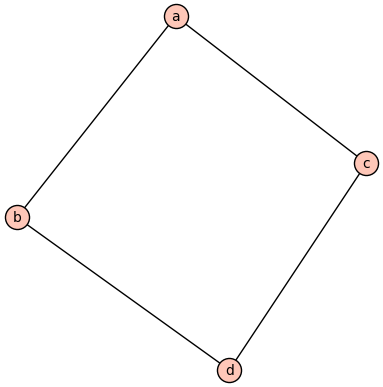
Raags have lots of nice properties, which you can see outlined in these articles (and others): 1, 2, 3. What are these nice properties? Well, as I’ve been alluding to for a while, the algebraic structure of $A(\mathrm{\Gamma })$ tends to faithfully capture the combinatorial structure of $\mathrm{\Gamma }$. Here by “capture” I mean that if $\mathrm{\Gamma }$ has some combinatorial property, then $A(\mathrm{\Gamma })$ will always have some associated algebraic property. By “faithfully” I mean that this is the only way for $A(\mathrm{\Gamma })$ can have this algebraic property. In other words, as far as these properties go, $A(\mathrm{\Gamma })$ only does what $\mathrm{\Gamma }$ forces it to. References for each of these examples can be found in link $3$ above:

• If $\mathrm{\Gamma }$ is the disjoint union of ${\mathrm{\Gamma }}_1$ and ${\mathrm{\Gamma }}_2$, then $A(\mathrm{\Gamma })=A({\mathrm{\Gamma }}_1)\ast A({\mathrm{\Gamma }}_2)$ is a free product (do you see why?). Moreover, this is the only way $A(\mathrm{\Gamma })$ is able to be a free product: If $A(\mathrm{\Gamma })=G\ast H$, then $\mathrm{\Gamma }$ is a disjoint union of two graphs, and $G$ and $H$ are their corresponding raags.

• If $\mathrm{\Gamma }$ is the join of two graphs ${\mathrm{\Gamma }}_1$ and ${\mathrm{\Gamma }}_2$, then $A(\mathrm{\Gamma })=A({\mathrm{\Gamma }}_1)\times A({\mathrm{\Gamma }}_2)$ (why?). Again, this is the only way $A(\mathrm{\Gamma })$ can decomopse as a direct product.

• $\mathrm{\Gamma }$ is a tree on $n$ vertices if and only if $A(\mathrm{\Gamma })$ is a nontrivial semidirect product of a free-group by $\mathbb{Z}$: $A(\mathrm{\Gamma })=F_{n-1}⋊\mathbb{Z}$.

• There is a (more complicated) algebraic condition which happens if and only if $\mathrm{\Gamma }$ has no full subgraph¹ equivalent to $P_4$ as above.

• There is an extremely complicated construction which identifies a family of expander graphs.

You might try to take your own favorite graph-theoretic concepts and see how they are reflected group-theoretically. Don’t be discouraged if you can’t show that your concept is represented faithfully – many of the above proofs involve a surprisingly deep toolkit. It’s still exciting to see what the characterization should be. As a more abstract bonus-exercise, here’s some weird food for thought: By analogy to the first two points above, a free product of any two groups is a kind of generalization of the disjoint union of two graphs. Similarly, the direct product is a kind of generalization of the graph-theoretic join.

---

Now that we understand what a raag is, the categorically minded among you might have a question: Is this a functor? And if so, what can we say about it?

Perhaps unsurprisingly, the answer to the first question is “yes”. The answer to the second depends on what category you think our graphs are living in. I claim there is a most natural choice of category, which I’ll describe in the next post. In the meantime:

---