Submodels vs Elementary Submodels
01 Oct 2020
I’m giving a GSS talk next week in the hopes of introducing myself to my new department. More importantly, I am giving this talk to try and showcase the utility of model theory in combinatorics and algebra. While writing this talk, I’ve been thinking about the best way to discuss elementary submodels as opposed to regular old submodels. When it was taught to me, a focus was placed on “quantifying over extra stuff”, which is true, but I was never shown a simple example. While I was thinking about how to teach it, I realized we can already find elementary and nonelementary submodels in graph theory, and that these might serve as good examples for people new to the area.
So, to begin, we have to talk about Models. I’m planning to write a longer form post on model theory at some point, but here are the basics.
We typically have functions, relations, and constants associated to any given
“structure” in mathematics. For groups, we obviously have the constant
When studying any fixed branch of math, the discourse is usually confied to formulas involving only some collection of symbols. Often we prove things by manipulating these symbols according to known rules, which are set out in axioms for how these symbols should behave. Model Theory studies what we can prove using only this information, and by formulating certain problems model theoretically, we can bring a lot of powerful machinery to bear.
To start, we have to fix the symbols of interest.
A Signature is a tuple
Then we can define the Language
- symbols from
- variables
- =
From your mathematical experience, you doubtless know intuitively how these symbols are allowed to fit together. However, for those wanting to see the precise definition, I’ve included one at this footnote 1.
Now that we know what formulas we are allowed to discuss (in a fixed language
Formally, a
Now that we know how to interpret the symbols of
Let’s look at the signature
Notice, however, that there is no restriction (yet) on our interpretation.
We could look at a nonstandard interpretation, say
In practice, though, we almost never work with bare models. We always ask that our
models satisfy some axioms
Today, though, we’re not talking about these techniques. We are instead
focusing on two notions of “submodel”, and talking about their differences.
We will focus on graphs, since they are simple combinatorial objects that
one can easily understand and play with. For us, a graph
will be a model for the signature
A submodel
Consider the following graph
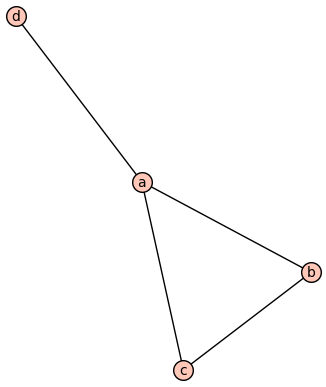
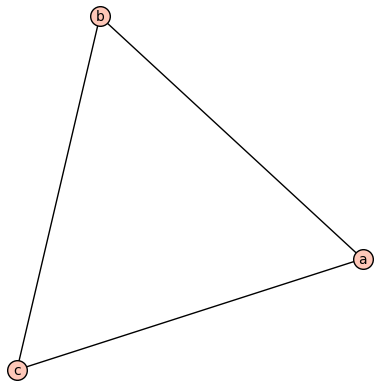
Then submodels are the induced or full subgraphs. Notably this is a submodel:
While this (the tripod
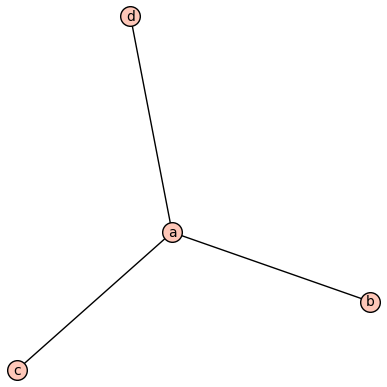
This fails to be a submodel beacsue its edge relation
As an algebraic example, consider the natural homomorphism
Submodels, though (and more generally embeddings)
preserve positive and negative formulas. Phrased differently, submodels both
preserve and reflect positive formulas. Phrased differently yet again,
if
But what, I hear you asking, about quantifiers? Notice it is not true
that submodels have to prserve the truth of formulas with quantifiers.
Intuitively, think about a formula
As a concrete example, consider the center
We can see similar behavior in graphs. For instance, the following graph has

However, the submodel which excludes
This brings us to a very special kind of submodel. A submodel
To show that a submodel is elementary, we have the
Tarski-Vaught Test,
which says that
It turns out there’s a reason there aren’t many simple examples of elementary submodels. Can you show that the only elementary subgraph of a finite graph is itself? (Hint: try to write down a formula which characterizes the graph up to isomorphism.)
This is true for more than just graphs, for the same reason. So any model with an elementary submodel must be infinite.
One easy example of an elementary submodel is
Since an elementary submodel
To get an example of this phenomenon, we can generalize the above example
slightly. Look at
As a second, less trivial example, consider the following graph
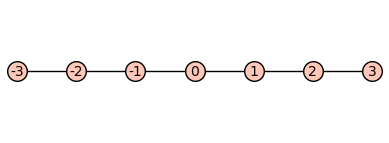
We can also consider the disjoint union

It turns out
There are lots of reasons elementary submodels are useful (for a famous example, see nonstandard analysis ), but it’s important to keep straight the difference between homomorphic images, submodels, and elementary submodels. I know I was tripped up by this for a long time, and a younger me would have been helped by these toy examples from graph theory.
As a last exercise, there is a strengthening of these results. Can you show
that, whenever
- if
- if
In words, universal formulas are “preserved downwards”, and existential formulas are “preserved upwards”.
-
We recursively define terms, which pick out particular elements of a model. Then we use terms to recursively define formulas, which are the actual objects of interest.
A term is defined recursively as follows:
- each variable
- each constant symbol
- given terms
A formula is defined recursively as follows:
- given terms
- given terms
- given formulas
- given a formula
formulas of the first two types are called atomic.
We can then define various other symbols as abbreviations:
- each variable
-
We first discuss how to interpret terms. Each term
- Variables
- Constants
- A term
Notice that we can assume
Next, we interpret formulas as subsets of
Again, we can always choose the free variables as
Since the other symbols
Finally, we write
As a (possibly fun) exercise, fix a signature
- Variables