Nilpotentizing Groups

28 Oct 2020

I really like group theory, and I’ve spent a lot of time reading about groups and their properties. Most of these properties seem like very natural things to consider ( $p$ -groups, abelian groups, simple groups, etc.) and the ones that don’t typically seem motivated by some external factor (solvable groups come to mind). However, I have always been somewhat confused by nilpotent groups. I know that they are “almost abelian”, and I can rattle off some facts about them and sketches of proofs… But it was never made clear to me how to work with them in practice. If I come across a nilpotent group in the wild, how does that help me? Surely I should be able to leverage the “almost abelian”-ness in a way that’s more general than “elements of coprime order commute”.

I figured out how the nilpotency assumption is helpful in computations last night, though I got on the topic in a rather roundabout way. I forget exactly how my brain moved between these ideas, but the basic outline was this:

The nilpotent groups of class $c$ (really class $\leq c$ ) form a variety by the HSP theorem
But this means there are some bonus axioms that we can add to the standard group axioms in order to carve out the class $c$ nilpotent groups. (In fact, since the $1$ nilpotent groups are exactly the abelian groups, we know the bonus axiom is $x y = y x$ in the case $c = 1$ )
So we should be able to “ $c$ -nilpotentize” a group in the same way we abelianize it by quotienting by the relations which force these new axioms to hold.

I spent some time thinking about what these new axioms might be, as well as some categorical questions: Is the subcategory of class $c$ nilpotent groups reflective in $Grp$ ? After all, $Ab$ is. But then I started thinking about why somebody might care about this construction. We care about the abelianization because it simplifies the group. It stands to reason that a nilpotentization might simplify the group with a slightly softer touch. By varying $c$ , we can control how big a quotient we want to take – this lets us trade simplicity of the quotient against fidelity to our original group! Immediately, there are two very natural questions that arise:

Can we actually $c$ -nilpotentize a group in practice? What do we quotient by?
How exactly are nilpotent groups are easier to work with than general groups? What does this construction really buy us?

It was in the process of understanding the second bullet that I felt like I started understanding some practical benefits of nilpotency.

As a fun game, can you show that $c Npt$ , the subcategory of class $c$ nilpotent groups, is reflective in $Grp$ ? You can see this abstractly if you know that every variety has free objects, so there is a “free class $c$ nilpotent group” on a given set $X$ ¹.

Remember, to show that $c Npt$ is reflective in $Grp$ , you want to show that there is a unique “ $c$ -nilpotentization” $G^{c Nil}$ so that every hom $G \to H$ with $H \in c Npt$ factors through $G^{c Nil}$ . In the case $c = 1$ , this is exactly the abelianization!

Let’s start with the second bullet and talk about what nilpotency buys us. We understand the class- $1$ groups (alias: abelian groups) well, so let’s take a look at class- $2$ groups.

Recall the Lower Central Series of a group $G$ is recursively defined by

$γ_{1} (G) = G$
$γ_{n + 1} (G) = [γ_{n} (G), G]$

Then $G$ is called Nilpotent (of class $c$ ) whenever $γ_{c + 1} (G) = 1$ . So, a nilpotent group of class $1$ is a group where $γ_{2} (G) = [G, G] = 1$ , and $G$ is abelian. This definition has always felt kind of opaque to me, but last night I realized what I was missing (and what was probably obvious to most other people):

g h = h g [g, h]

This wholly obvious fact says that we can commute any two elements provided we pick up a factor of $[g, h]$ . In this way, $[g, h]$ measures how $g$ and $h$ fail to commute.

Now, in an abelian group, $[g, h] = 1$ for all $g, h$ . So we can commute with impunity. In a group of class $2$ this can fail, but we know that $γ_{3} (G) = 1$ . That is, $[[G, G], G] = 1$ . Said yet another way, $[[g, h], k] = 1$ for every $g, h, k$ ! So sure we might pick up a commutator fudge factor, but this fudge factor will commute with everything!

Concretely, this means we can always push commutators to one side!

g h k = h g [g, h] k = h g k [g, h]

So in a group of class $2$ , we can rearrange our product as much as we want as long as we promise to multiply by a fudge factor from $[G, G]$ at the end. For any permutation $σ$ :

g_{1} g_{2} \dots g_{n} = g_{σ (1)} g_{σ (2)} \dots g_{σ (n)} h

for some $h \in [G, G]$ depending on $σ$ .

Similarly for groups of class $3$ . Now $[G, G, G, G]$ is trivial², so our commutators may not be central, but our “second order” commutators are:

g h k = h g [g, h] k = h g k [g, h] [[g, h], k]

In this instance, the “second order” fudge factor $[[g, h], k]$ (often written as $[g, h, k]$ – see the earlier footnote) will commute with everything.

It is clear that these get hairy fairly quickly, but it makes the entire concept feel (at least to me) more concrete. It also makes clear how this is a generalization of abelianness - when we commute things, the resulting fudge factors are easy to control. Of course, the degree of “easiness” decreases fairly quickly as the nilpotency class $c$ increases. For $c = 2$ , though, this seems like a viable object to study if one is looking to simplify a group!

So how might we find the nilpotentization of $G$ ? Earlier on in the post I alluded to some abstract nonsense which will give us the result (It probably says something about me that this was the proof my sleep-deprived brain first reached for). However, now that we’ve remembered the lower central series definition of a nilpotent group, there is a much cleaner, down-to-earth approach:

$G^{c Nil} = G / γ_{c + 1} (G)$

We simply force $γ_{c + 1} (G) = 1$ . This is directly analogous to the abelianization, since $γ_{2} (G) = [G, G]$ ! It takes a tiny argument to show that any group homomorphism $G \to H$ with $H$ of class $c$ factors through $G^{c Nil}$ , but I’ll leave this verification as a cute exercise.

One thing I will touch on, though – Why can we quotient by $γ_{c + 1} (G)$ ? Is it obvious that these groups are always normal? I certainly don’t think so! But, it turns out that $γ_{c + 1} (G)$ shares lots of nice properties with $[G, G]$ .

Here is (for me) the easiest way to see what I mean: Just like $[G, G] = γ_{2} (G)$ is generated by $⟨ [g, h] ⟩$ , it turns out $[G, G, G] = γ_{3} (G)$ is generated by $⟨ [[g, h], k] ⟩$ ! In fact, $γ_{n} (G)$ is generated by $⟨ [g_{1}, \dots, g_{n}] ⟩$ (again, using the notation from the footnote).

But this is fantastic! We know that subgroups of this form are called verbal and they satisfy lots of very nice properties ³! In particular, all verbal subgroups are characteristic, thus normal.

As one last question, we might ask how easy it is to compute with these nilpotentizations. Luckily, there are some efficient implementations of these results. You can read more about these algorithms here, but the tldr is:

Magma has functions like $NilpotentQuotient (G, c)$ which computes the class $c$ nilpotentization of $G$ . (Documentation here)
GAP has the $NQ$ package, which also has a $NilpotentQuotient (G, c)$ function. (Documentation here)

Since GAP ships built-in with Sage, we have access to these algorithms in our favorite computational tool. Unfortunately, the $NQ$ package wasn’t included in my sage installation by default – I had to install gap-packages via pacman in order to get it.

With that subtle point out of the way, let’s see it in action. Since the sage cloud server I use doesn’t play nice with the GAP console, I can only include a screenshot. You should definitely experiment with this stuff yourself, though!

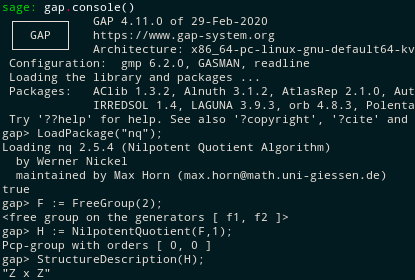
Some GAP code running inside of sage

Notice we asked for the class $1$ nilpotentization of $F_{2}$ , and GAP correctly gave us $Z^{2} = F_{2}^{ab}$ !

In the case of finite groups, we can write dumber code in pure sage:

xxxxxxxxxx
 
from itertools import combinations_with_replacement
​
def Nilpotentize(G,c):
    """
    Return the nilpotent quotient of class c.
    
    Only works for finite groups G!
    """
    def iterated_commutator(gs):
        """
        computes [g1, g2, ... gn] from a list gs
        """
        comm = gs[0]
        for g in gs[1:]:
            comm = comm.inverse() * g.inverse() * comm * g
        return comm
    
    # Get the subgroup generated by the iterated commutators
    toKill = G.subgroup([iterated_commutator(gs) for gs in combinations_with_replacement(G.list(),c+1)])
​
    return G.quotient(toKill)

Help | Powered by SageMath

Messages

I only wrote this code today, so I haven’t had time to play around with it yet. Here are some fun questions I have for myself, which you might also want to think about!

Where do the various $γ_{n} (G)$ show up in the lattice of subgroups of $G$ ?
For finite groups, the decreasing chain $γ_{n} (G)$ must eventually stabilize. Given a group $G$ , can we predict for which $n$ this will happen?
What can we say about a group $G$ if we know the chain $γ_{n}$ stabilizes quickly? Stabilizes slowly?

There’s lots of interesting questions one gets by playing around with these groups! Let me know in the comments if you think of any of your own ^_^

Free nilpotent groups seem to be well studied, and fairly complicated! This is one excellent example of abstract nonsense providing the existence of a free object whose combinatorial description is… unpleasant. You can read Terry Tao’s description of them here. ↩
Here we define $[G, G, G, G] = [[[G, G], G], G]$ . This seems to be standard in the literature, and we can do it at the element level too: $[g, h, k] = [[g, h], k]$ . Notice this is not associative! $[[g, h], k] \neq [g, [h, k]]$ so we must remember to associate left! ↩
This is a kind of syntax-semantics relationship. One day I want to make a post talking about syntax and semantics, and in particular some real-world ways where this duality arises (even if somewhat informally). In the mean time, trust that this result is part of a larger pattern of spiritually related results. ↩