Limsups and Liminfs of Sets

08 Nov 2020 - Tags: quick-analysis-tricks

I’m in a measure theory class right now, and I think it’s important to be properly comfortable with measure theory in a way that I’m currently not. It has deep connections with things that I find very interesting (Descriptive Set Theory, Ergodic Theory, their intersection in Amenable Groups, etc.) and it’s one of my go to examples of an “obviously useful” branch of math. If you can apply your interests to measure theory somehow, I think that’s a compelling argument to fend off questions of “why is this worthwhile” (at least from other mathematicians).

All this to say I’ve started reading more measure theory books, though it makes my pile of unread logic and algebra books sad. In particular I bought a copy of Halmos from an online used bookstore for $8 (!!), and it’s a fantastic read so far. I wanted to highlight one particular observation that, while obvious in hindsight, was extremely helpful for me. Hopefully by posting about it here, I’ll also find it more memorable. While this isn’t a “trick” in the same sense as the other posts in this series, I still feel like it fits here.

If $(E_{n})$ is a sequence of sets, then

$lim sup E_{n}$ is the set of $x$ that appear in infinitely many $E_{n}$
$lim inf E_{n}$ is the set of $x$ that appear in all but finitely many $E_{n}$

I think I didn’t see this because I was too focused in on generalizing my understanding of $lim inf$ and $lim sup$ of sequences $(x_{n})$ . In the case of real sequences, $lim inf$ is the smallest thing some subsequence converges to, while $lim sup$ is the biggest thing some subsequence converges to. I think the following image does a good job showing what I mean:

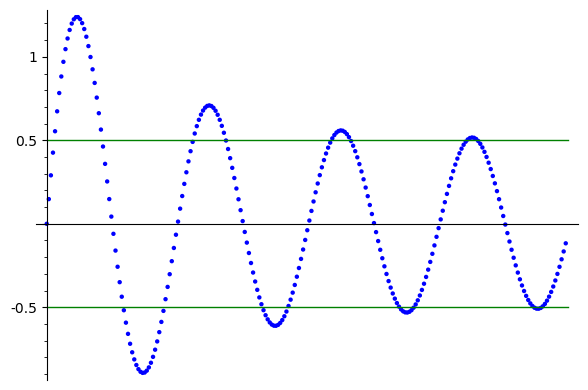
a plot showing limsup and liminf

If this is your sequence $x_{n}$ , then the biggest thing you can possibly converge to is $\frac{1}{2}$ . Similarly, the smallest thing you can possibly converge to is $- \frac{1}{2}$ . So these are $lim sup x_{n}$ and $lim inf x_{n}$ respectively. From this point of view it is clear that $lim inf x_{n} \leq lim sup x_{n}$ , and whenever they are equal, $lim x_{n}$ exists and agrees with them both.

Here $lim inf x_{n} = lim_{n \to \infty} inf_{m > n} x_{m}$ , and dually, $lim sup x_{n} = lim_{n \to \infty} sup_{m > n} x_{m}$ . This, of course, is where the notation comes from, but I think a better definition is

$lim sup x_{n} = inf_{n} sup_{m > n} x_{m}$
$lim inf x_{n} = sup_{n} inf_{m > n} x_{m}$

Not only does this make it much more obvious that these definitions are dual, it more readily generalizes to the definition for sets:

$lim sup E_{n} = ⋂_{n} ⋃_{m > n} E_{m}$
$lim inf E_{n} = ⋃_{n} ⋂_{m > n} E_{m}$

(As a quick check in – why are the two definitions of $lim inf x_{n}$ equivalent?)

Because I liked my intuition for $lim sup$ and $lim inf$ of sequences of reals, I’d been viewing $lim inf$ and $lim sup$ of sets as “the smallest (resp. largest) set that $E_{n}$ could converge to”… Of course, I have no intuition for what it means for a sequence of sets to converge! Because of this, until today I’ve had little to no intuition for what these sets actually are.

As with all realizations, I should have seen this much sooner. It’s a common trick in descriptive set theory to pass between logical constructors and set theoretic operations. These are entirely natural, and correspond to a correspondence between the (syntactic) boolean algebra of propositions, and the (semantic) boolean algebra of sets. Yet again I’m talking about syntax and semantics on this blog, and yet again I’m promising a post detailing a few of my favorite examples. For now though, let’s write this one example out explicitly: Say we have a family of properties $P_{n}$ . Then

${x ∣ P_{0} \land P_{1}} = {x ∣ P_{0}} \cap {x ∣ P_{1}}$ (conjunction corresponds to intersection)
${x ∣ P_{0} \lor P_{1}} = {x ∣ P_{0}} \cup {x ∣ P_{1}}$ (disjunction corresponds to union)
${x ∣ \neg P_{0}} = {x ∣ P_{0}}^{c}$ (negation corresponds to complementation)
${x ∣ T} = X$ (“true” corresponds to the whole set)
${x ∣ F} = \emptyset$ (“false” corresponds to the empty set)

Quantifiers might seem tricky at first, but notice $\forall n . P_{n}$ is really the same thing as $P_{0} \land P_{1} \land P_{2} \land \dots$ and so:

${x ∣ \forall n . P_{n}} = ⋂_{n} {x ∣ P_{n}}$
${x ∣ \exists n . P_{n}} = ⋃_{n} {x ∣ P_{n}}$

This trick works more broadly too¹. For any index set $I$ , we have

${x ∣ \forall α \in I . P_{α}} = ⋂_{I} {x ∣ P_{α}}$
${x ∣ \exists α \in I . P_{α}} = ⋃_{I} {x ∣ P_{α}}$

Since we only know that countable setwise operations are allowed in measure theory, much of descriptive set theory amounts to showing that certain quantifiers only need to range over countable sets.

Of course, through this lens, the description in Halmos is obvious:

lim sup E_{n} = ⋂_{n} ⋃_{m > n} E_{n} = {x ∣ \forall n . \exists m > n . x \in E_{n}} = {x ∣ x \in E_{n} for infinitely many n}

Do you see why this also shows that $lim inf E_{n} = {x ∣ x is in all but finitely many E_{n}}$ ?

This viewpoint is useful not only in understanding what $lim sup E_{n}$ and $lim inf E_{n}$ are, it’s useful in proving things about them! Let $E_{n}$ be a sequence that alternates between two sets $A$ and $B$ . Is it obvious that $lim sup E_{n} = A \cup B$ and $lim inf E_{n} = A \cap B$ ? Now look only at the definitions – is it only obvious from those?

I think this lens sheds some light on $lim inf$ and $lim sup$ of real sequences too. I’ll leave it to you to work through the quantifiers, but it turns out that $lim sup x_{n}$ is the smallest number $x^{*}$ so that infinitely many $x_{n}$ are bigger than $x^{*}$ . This is the central observation in the proof of the Cauchy-Hadamard Theorem, and it’s nice to see that this observation is actually obvious (in this interpretation of $lim sup$ ).

Dually, $lim inf x_{n}$ is the biggest number $x_{*}$ so that infinitely many $x_{n}$ are smaller than $x_{*}$ . As a last puzzle – why doesn’t $lim inf x_{n}$ have a “all but finitely many” flavor like $lim inf E_{n}$ does? Can you find a sense in which it does?

It turns out viewing quantifiers as generalized conjunctions/disjunctions works very broadly! This is a useful viewpoint to take in many settings throughout logic. In $L_{ω_{1}, ω}$ for instance, this trick lets us use natural number quantifiers (even though the language might not technically allow them). This lets us express, say, that a group is finitely generated by writing every element as a word in the generators (and there’s only countably many such words!) ↩