A Wild Arctan Formula

23 May 2021

Yesterday a good friend of mine sent me the following bizarre formula:

4^{1 / π} = lim_{n \to \infty} \frac{π}{2 \arctan (n)} \frac{π}{2 \arctan (n + 1)} \frac{π}{2 \arctan (n + 2)} \dots \frac{π}{2 \arctan (2 n)}

This is listed as formula $(130)$ at the bottom of the wolfram mathworld page on formulas for $π$ , where it is called “A fascinating result due to Gosper”. There are $3$ citations for Gosper on that page, but I can’t actually figure out how to see any of them. That’s fine, though – We’ll just have to prove it ourselves. I ended up heavily using computer tools (by which, of course, I mean sage) to crack this, and it almost felt like cheating (since I knew my friend was doing it by hand). But I hope that, in addition to showing off a cool formula, this blog post can showcase how one might use sage to solve problems in the wild (even though in this case we used sage in a fairly mundane way).

First let’s rewrite this product a little bit more compactly. We want to show

lim_{n \to \infty} \prod_{k = n}^{2 n} \frac{π}{2 \arctan (k)} = 4^{1 / π} .

I only know one way to handle limits of products, so let’s hit everything in sight with $\log$ and work with a sum instead. We now want to show

lim_{n \to \infty} \sum_{k = n}^{2 n} \log (\frac{π}{2 \arctan (k)}) = \log (4^{1 / π}) = \frac{\log (4)}{π} .

We know that as $k \to \infty$ , $\arctan (k) \approx \frac{π}{2}$ , so the thing we’re logging is getting close to $1$ , and so our summands are getting close to $0$ . That’s a good sign, but if we want to really compute these things we need to understand quantitatively how close to $0$ we really are.

My first instinct is to taylor expand at infinity. That is, let’s write

f (x) = \log (\frac{π}{2 \arctan (1 / x)})

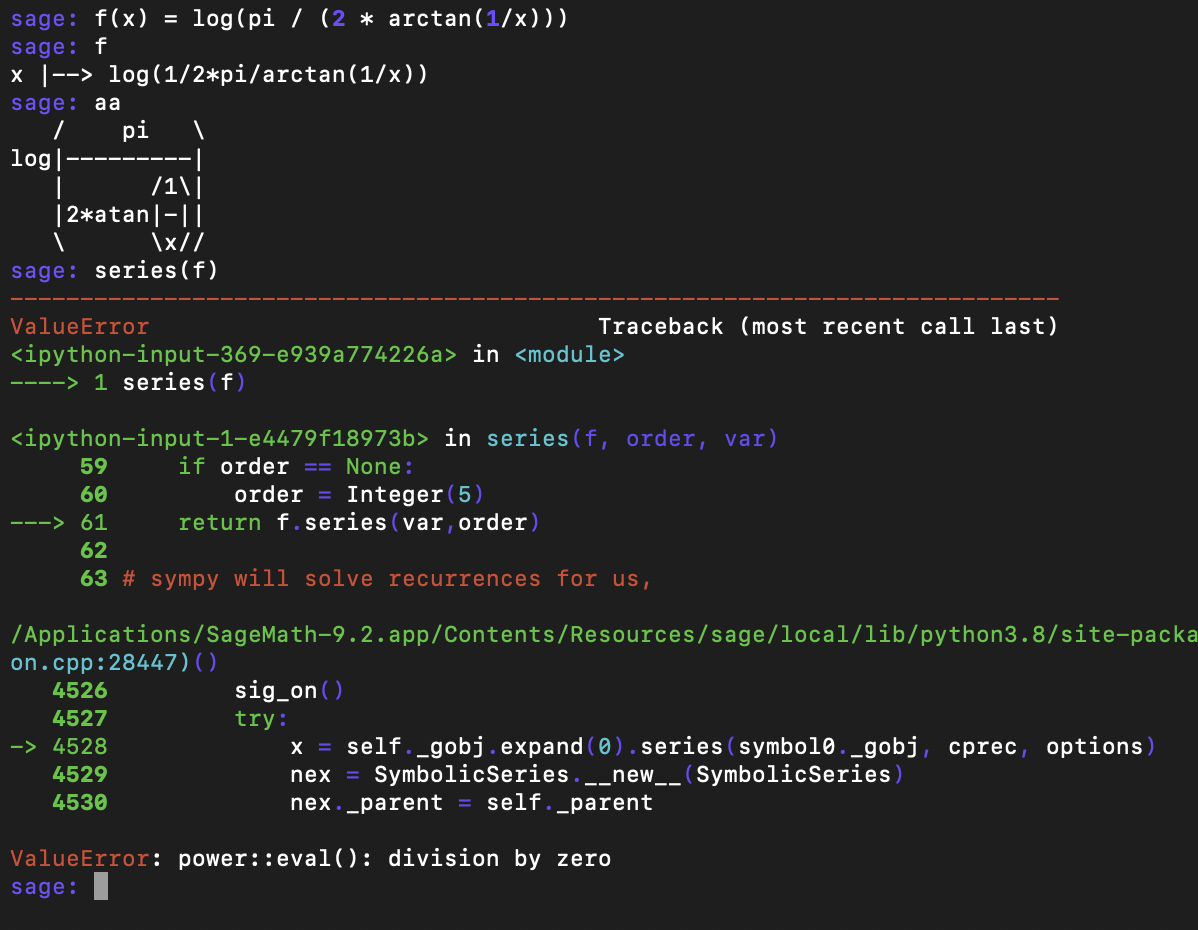
and expand this at $x = 0$ . This corresponds to taylor expanding our actual summand “near $k = \infty$ ” since $x = 1 / k \approx 0$ when $k \approx \infty$ . I have a custom function¹ in my init.sage to automatically compute a series expansion at $0$ , but for some reason it doesn’t work with this²:

So we do some googling for $\arctan (1 / x)$ , and we land on the following really fun formula:

\arctan (x) + \arctan (1 / x) = π / 2 (for x > 0) .

This is really neat (and has a nice geometric proof), and lets us rewrite our function as

f (x) = \log (\frac{π}{2 (π / 2 - \arctan (x))}) .

Sage will happily give us a series expansion of this and we learn

f (x) = \frac{2 x}{π} + O (x^{2}),

so our sum becomes

lim_{n \to \infty} \sum_{k = n}^{2 n} f (1 / k) = lim_{n \to \infty} \sum_{k = n}^{2 n} (\frac{2}{π k} + O (1 / k^{2})) .

But now we’re basically done! Our error term vanishes in the limit, since $\sum_{k = n}^{2 n} 1 / k^{2}$ is bounded by the tail of a convergent sequence. Then we pull out the factor of $2 / π$ , and we find our sum is

\frac{2}{π} lim_{n \to \infty} \sum_{k = n}^{2 n} \frac{1}{k} = \frac{2}{π} lim_{n \to \infty} H_{2 n} - H_{n}

where $H_{n}$ is the $n$ th harmonic number.

We know that $H_{n} \sim \log (n)$ , and so $H_{2 n} - H_{n} \sim \log (2 n) - \log (n) = \log (2)$ in the limit.

This, at last, tells us that our sum is

\frac{2}{π} \log (2) = \log (4^{1 / π})

and so our product is

4^{1 / π}

as desired.

Notice nothing we did was hard. Not only does this show the power of calculus (I feel like the more math I learn the more I respect basic calculus), it also shows the power of sage to quickly and easily do things like taylor expansions for us. Of course, with some extra time to think about the problem, I’ve come up with a way you could see this without needing to taylor expand anything too tricky³, but before you polish the edges of a proof, it’s nice to have something, and sage really makes that “first draft” version of a proof easier to find.

Which you can find in my dotfiles ↩
While writing this blog post, I tried the taylor series implementation, and it actually did work!

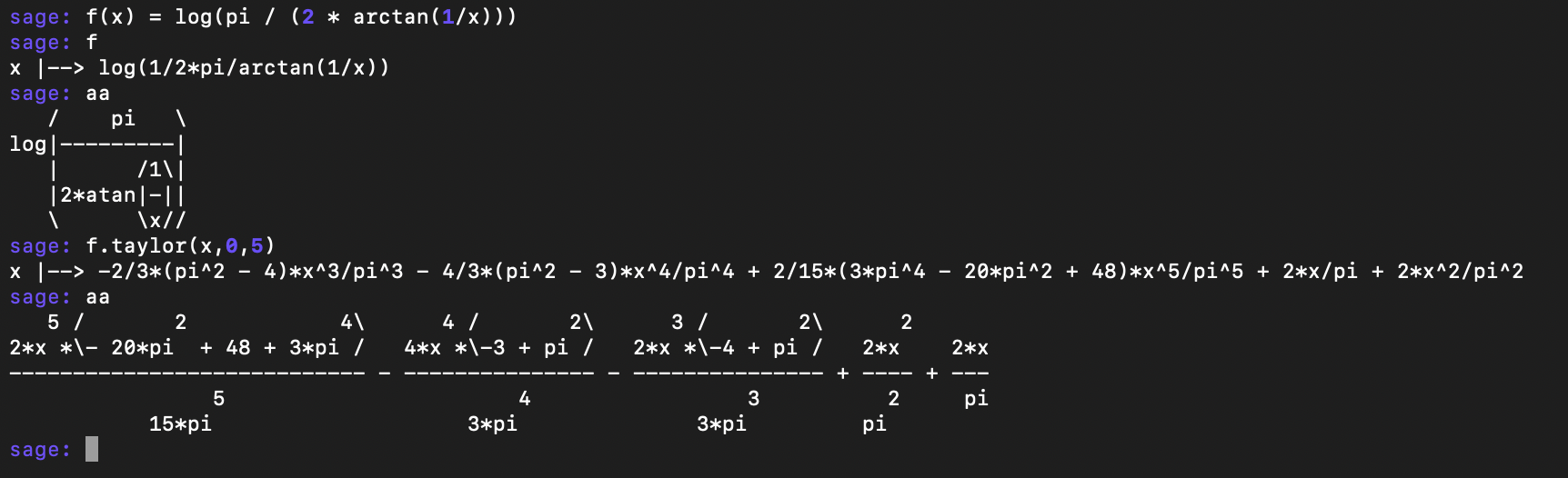
This would have made the whole process go a bit more smoothly, but we wouldn’t have learned the fun formula, so I’m weirdly glad that the power series implemtation has slightly different behavior from the taylor series implementation… Presumably because one is formal, while one is analytic?

It is nice that sage could have directly told us that our summand looks like $\frac{2 x}{π} + O (x^{2})$ , though, and I guess this means I’ll have to modify my series code to call the taylor command if calling series throws an error. ↩
It’s pretty clear that near $0$ we should have $\arctan (x) \sim x$ . You can basically read this off a graph, or you could remember $\frac{d}{d x} \arctan (x) = \frac{1}{1 + x^{2}}$ and evaluate at $0$ .

Next we’ll need the fun fact from above, that $\arctan (x) + \arctan (1 / x) = π / 2$ for positive $x$ , as well as a famous generating function that in hindsight I actually have memorized:
$\log (\frac{1}{1 - x}) = 0 + \frac{1}{1} x + \frac{1}{2} x^{2} + \frac{1}{3} x^{3} + \dots$
Putting these facts together, we can pretty quickly get
$\begin{aligned} f (x) & = \log (\frac{π}{2 (π / 2 - \arctan (x))}) \\ = \log (\frac{π}{π - 2 \arctan (x)}) \\ = \log (\frac{1}{1 - \frac{2}{π} \arctan (x)}) \\ \sim \log (\frac{1}{1 - \frac{2}{π} x}) \\ = \frac{2 x}{π} \pm O (x^{2}) \end{aligned}$
and we could finish off the proof from here.

Note, though, that even though we avoided sage (or otherwise computing an awful taylor expansion by hand), the price we paid was more background knowledge. I happened to know this series, as well as this trick for swapping $\arctan (x)$ with $\arctan (1 / x)$ , but there are lots of places where I definitely would not know the relevant tricks. Obviously it’s still good to know lots of these little tricks, and computer algebra systems are no excuse for a familiarity with the objects you’re studying. But it can be really helpful for mindless computation all the same.

Alright, I’ll get off my soapbox now :P ↩