A geometric proof that $D_{2m}\le {\mathfrak{S}}_n$ is possible for $m>n$

16 Aug 2021

To nobody’s surprise, I was on MSE tonight, and saw a simple question about group theory. The original question doesn’t matter as much as a question it made me wonder to myself:

Intuitively it feels like the answer should be “yes”, but I wasn’t able to come up with a proof myself. Thankfully it didn’t take much googling to find an excellent example due to pjs36. I’ll show it for completeness, but you can find the original post here.

The idea is to embed $D_{12}$ in ${\mathfrak{S}}_5$ by working with subpolygons instead of vertices. This is analogous to showing the symmetry group of a cube is ${\mathfrak{S}}_4$ by looking at the diagonals inside the cube, rather than looking at the vertices/edges/faces individually.

Since a picture is worth a thousand words, I’ll steal pjs36’s picture:

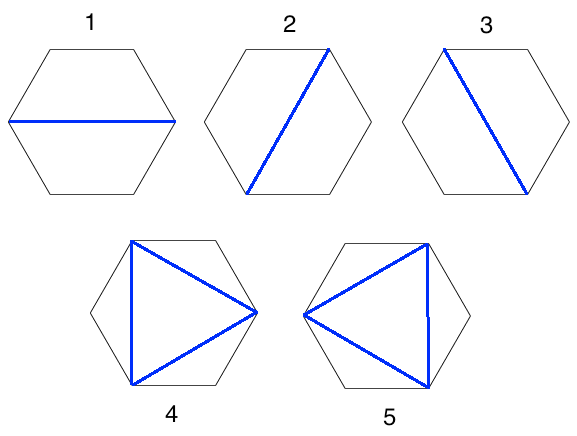
If you know where these $5$ subpolygons get sent, you actually know where the whole hexagon gets sent! This witnesses $D_{12}\le {\mathfrak{S}}_5$ in a starkly beautiful way.

It got me wondering, though. Can we run a similar argument to get $D_{2m}\le {\mathfrak{S}}_n$ for other choices of $m$? Since you’ve read the title of this blog post, you know the answer is “yes”¹. But at this point I should issue a quick clarification: This (very clever!) idea is not actually my own – I found it in yet another mse post. I was already planning on writing up a blog post about this problem, but when I found the solution I knew I had to talk about it. Now, let’s talk through how we might have solved this problem ourselves:

Obviously if $p$ is prime, then $D_{2p}$ first shows up as a subgroup of ${\mathfrak{S}}_p$ in the natural way (by permuting the vertices). We can’t do any better than this since for $p$ prime, $p\nmid n!$ for any $n<p$.

A moment’s thought (or more likely, quite a few moments’ thoughts) shows that actually $D_{2p^k}\nleqq {\mathfrak{S}}_n$ for $n<p^k$. The idea here is that $D_{2p^k}$ has a $p^k$ cycle. The order of an element $\sigma \in {\mathfrak{S}}_n$ is the $\text{lcm}$ of the cycle lengths in $\sigma$, so even though $p^k$ might divide $n!$, there’s no way to get an $\text{lcm}$ of things $<p^k$ to equal $p^k$.

Pjs36’s solution feels like it should generalize, and looking more carefully at the pictures above, we’re considering the $2$-gons and $3$-gons living inside of our $6$-gon… This idea links up well with our counterexamples from earlier, since the subpolygons of an $m$-gon are exactly the $\ell$-gons for $\ell \mid m$ and prime powers are special in the divisibility order.

We want to make $n$ (the number of generators of our symmetric group) as small as possible, so we should make the subpolygons we look at as big as possible (so that there aren’t many). Since we know from our earlier investigation that $p^k$-gons are the obstruction to “shrinking” $n$, whatever construction we do should give us $p^k$ objects to permute when we look at a $p^k$-gon.

Eventually, this might lead us to consider the $p^k$ many $\frac{m}{p^k}$-gons living inside our $m$-gon. In the $p^k$-gon case, this means we’re considering the $p^k$ many $1$-gons (that is, just the vertices), which is exactly what we expect. In the $6$-gon case, this mean we consider the $\frac{6}{2}$-gons and the $\frac{6}{3}$-gons, but this is exactly pjs36’s original example! In the case of a $2^3\cdot 3^2\cdot 5$-gon, this means we’re looking at the $45$-gons (there’s $8$ of them), the $40$-gons (there’s $9$ of them), and the $72$-gons (there’s $5$ of them). Notice here how we’re able to keep the number of objects small (there’s only $8+9+5=22$ things we’re permuting) by keeping our subpolygons big.

In general, let’s write $m=\prod P_i$ where each $P_i=p_i^{k_i}$ is a (maximal) prime power. We can find $P_i$ many $\frac{m}{P_i}$-gons living inside our $m$-gon, and every symmetry of our $m$-gon permutes these subpolygons amongst themselves. That is, we get a permutation in ${\mathfrak{S}}_{P_i}$ for each $i$.

Next, we can glue these together into a map

$$D_{2m}\to \prod {\mathfrak{S}}_{P_i}.$$

which I claim is actually injective.

To see why, say that some $g\in D_{2m}$ is in the kernel of the above map. Then it’s in the kernel of each $D_{2m}\to {\mathfrak{S}}_{P_i}$, so $g$ fixes each of our subpolygons. But this can only happen if $g$ fixes the entire $m$-gon, so $g=1$ and our map is injective.

Now we see the light at the end of the tunnel! We have an embedding $D_{2m}\hookrightarrow \prod {\mathfrak{S}}_{P_i}$, and we want an embedding $D_{2m}\hookrightarrow {\mathfrak{S}}_n$ for some $n$. But there’s an “obvious” way to do this! If you have a permutation of $k$ objects and a permutation of $\ell$ objects, we can just put them next to each other and call it a permutation of $k+\ell$ objects.

Using this “put them next to each other” embedding, we see that

$$D_{2m}\hookrightarrow \prod {\mathfrak{S}}_{P_i}\hookrightarrow {\mathfrak{S}}_{\sum P_i}.$$

So $D_{12}$ embeds in ${\mathfrak{S}}_{2+3}={\mathfrak{S}}_5$, as we’ve seen. Likewise, each $D_{2p^k}$ embeds in ${\mathfrak{S}}_{p^k}$, which agrees with our earlier experiments. Finishing our concrete example from earlier shows $D_{2\cdot (2^3\cdot 3^2\cdot 5)}$ embeds in ${\mathfrak{S}}_{2^3+3^2+5}={\mathfrak{S}}_{22}$, which is much smaller than the obvious ${\mathfrak{S}}_{2^3\cdot 3^2\cdot 5}={\mathfrak{S}}_{360}$!

As one last question: how much smaller is it? If $m=\prod p_i^{k_i}$, then let’s call each $p_i^{k_i}$ a Principal Divisor of $m$. Moreover, let’s write

$$s^{\ast }(m)=\sum p_i^{k_i}.$$

According to Upper Bounds on the Sum of Principal Divisors of an Integer by Eggleton and Galvin (up to change of variable name, to be consistent with the other variables in this post):

If $m$ is any positive integer with $\ell \ge 2$ principal divisors, and each greater than $\ell /2$, then

$$s^{\ast }(m)\le \frac{m}{{\ell }^{\ell -2}}.$$

Moreover, this holds with equality when $m=30$.

This tells us that we can embed $D_{2m}$ in a symmetric group with generators that shrink rapidly as the number of principal divisors of $m$ increases (provided each is not individually too small).

---