Talk - Bring Out the Crayons -- A Survey of Descriptive Combinatorics

10 Nov 2021 - Tags: my-talks

Last week Jacob asked me to give a talk in the topology seminar for UCR. I’ve been pretty busy lately, but I have a reputation to uphold, so I agreed, even though I didn’t have a great idea of what I wanted to talk about. My first idea was to talk about modal logic, which admits a nice topological semantics, but I wasn’t able to come up with any ways the logic was able to give us extra information topologically. It was always to topology helping to say things about the logic, and that’s not really the direction I wanted the ideas to flow for this talk. I considered talking about locales, but I’m still not super familiar with locales and I was worried I wouldn’t be able to answer some of the questions that might get asked. Most worryingly, I don’t have a good answer for “why should I care?”. I personally think locales are cool, and there’s good reasons to care if you’re already sold on constructive mathematics and toposes… But it’s hard to justify to a generic mathematician on the street¹. Eventually, I settled on Descriptive Combinatorics, an extremely interesting topic in its own right, and one which has lots of interesting ties to geometric group theory.

So then, what did we talk about?

We started with the definition of a graph as $G \subseteq X \times X$ , and a ( $k$ -)coloring as a function $c : X \to k$ so that $x G y ⟹ c x \neq c y$ . Then we proved a graph is $2$ -colorable if and only if it has no odd cycles. This is a classical result in combinatorics, and we can pass to the setting of infinite graphs by using the axiom of choice (we could use a compactness argument, but maybe it’s easier to choose a starting vertex from each connected component). The fact that we need AC, though, tells us that our coloring is “nonconstructive”, and it’s natural to ask if there’s a constructive way to get such a coloring… But what does that even mean?

Enter Descriptive Set Theory, which has a lot of tools for showing what constructions are “definable”, and which has a preexisting language for discussing these kinds of problems. The idea is to say something is definable provided we can build it in a measurable way². This is loosely inspired by the famous Solovay Model, which shows that we need AC in order to build nonmeasurable things. So if we’re able to build something in a measurable way, it’s (very informally) reasonable to say it must be “definable”³.

So now we move to the natural setting for descriptive set theory: we work with a polish space $X$ with a graph $G \subseteq X \times X$ , that we now require to be borel. I gave some examples of polish spaces to show that they’re extremely common⁴, and then asked if a borel graph $G$ with no odd cycles must have a borel $2$ coloring. The answer, it turns out, is no!

The proof is quick if you know some ergodic theory⁵:

$⌜$ Let $T : S^{1} \to S^{1}$ be an irrational rotation by some angle $α$ . Now let $G \subseteq S^{1} \times S^{1}$ so that $x G y ⟺ x = y \pm α$ .

Then $G$ decomposes $S^{1}$ as continuum many copies of the cayley graph of $Z$ . In particular, there are no odd cycles. But if we had a decomposition of $S^{1}$ into two lebesgue measurable color classes, say $R$ and $B$ , then we have a problem.

First, notice $m (R) = m (B)$ , since $T$ is measure preserving and swaps $R$ and $B$ . Moreover, notice $T^{2} (R) = R$ and $T^{2}$ is ergodic. So $R$ must either be null or co-null. But if $R$ and $B$ are null, then they can’t cover $S^{1}$ , and if $R$ and $B$ are co-null, they must intersect. $⌟$

This shows there is no lebesgue measurable $2$ -coloring of this graph, and thus no borel coloring. A similar argument shows that there is no baire measurable coloring either. Notice that we have to choose a basepoint for each of our cayley graphs of $Z$ , because our orbits are really torsors (which are to groups as affine spaces are to vector spaces).

I ended the talk with a natural question: Why should we care?

I’m interested in descriptive combinatorics because I think it’s cool to see what changes between the finite case and the infinite case when we require things to be definable. But I understand that not everybody likes combinatorics for its own sake, and since this seminar has a lot of geometric group theorists, I wanted to show them why they might care. Thankfully, I remember watching a talk a while ago which has a nice application to amenabilitiy. This is a bit more broad than definable colorings (we’re looking at definable matchings instead), but it’s a similar flavor.

So I recalled the definition of a paradoxical decomposition, and showed that we can paradoxically decompose the cayley graph of $F_{2}$ . See the picture below⁶:

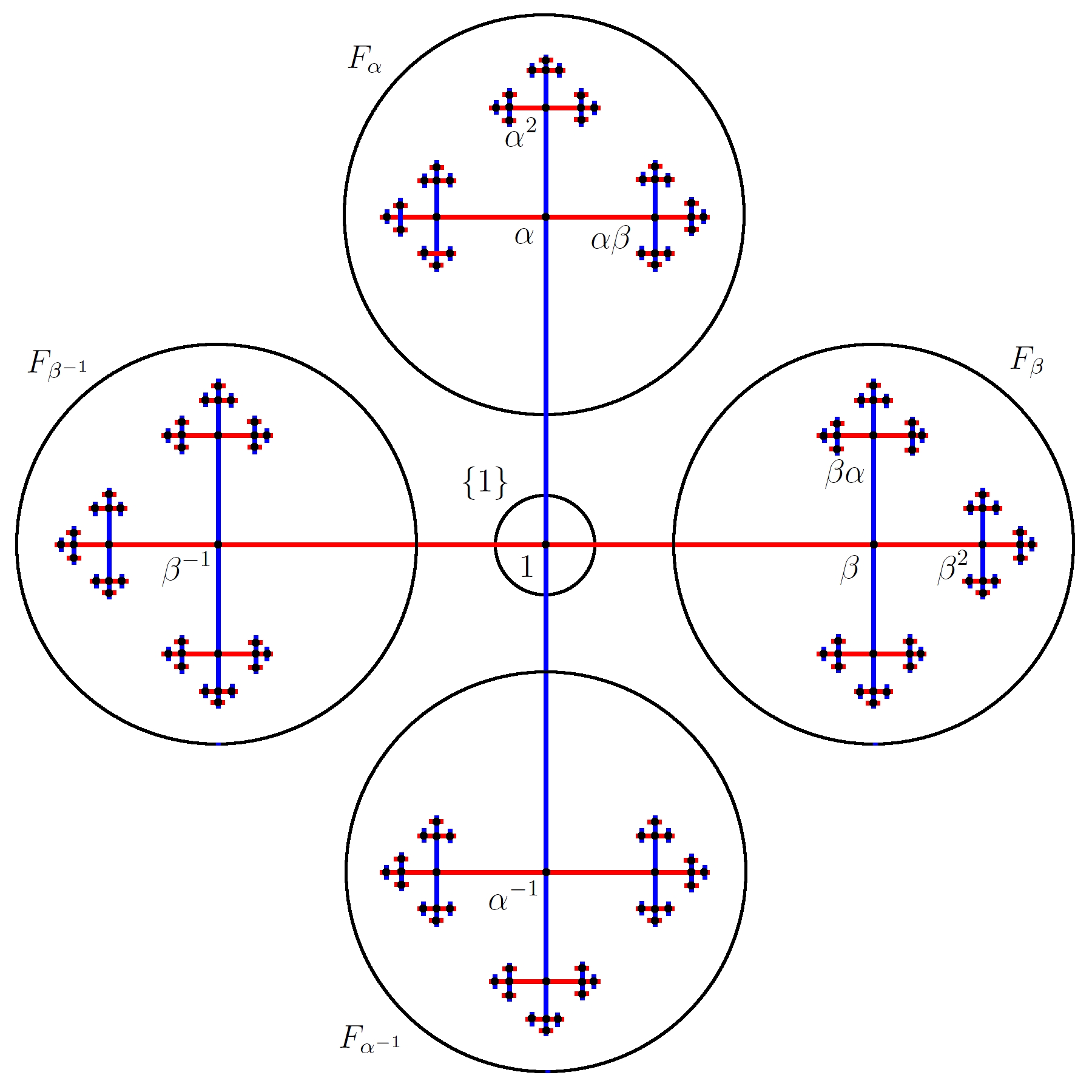
We can use just the left and right pieces (or indeed just the top and bottom) to reconstruct the entire graph. See this picture⁷ (and try to ignore the fact that the roles of $α$ and $β$ have swapped with the roles of $a$ and $b$ … This is what I get for lazily frankensteining other people’s graphics together).

Translating the left piece by $a$ and then combining it with the right piece gives the entire space. Similarly, translating the bottom piece by $b$ and combining it with the top piece gives the entire space too! So we were able to break our space into $5$ pieces, move them around, and get two copies of our space!

It turns out that this is basically the Banach-Tarski Paradox! We let $F_{2}$ act freely on $S^{2}$ . Then this decomposes $S^{2}$ into an uncountable disjoint union of orbits, each of which looks like the cayley graph of $F_{2}$ . So by running the above decomposition simultaneously in each orbit (using AC to choose a basepoint in each torsor again) we get the desired decomposition.

To finish up, I showed how this decomposition (and thus concepts like amenable groups and paradoxical decompositions) can be linked to descriptive combinatorics:

Let $a : Γ ↷ X$ be an action of a group $Γ$ on a space $X$ . Then for $S$ a finite subset of $Γ$ , we can form the graph $G (a, S)$ whose vertex set is $X ⊔ X ⊔ X$ and where we connect a point $x$ in the first copy of $X$ to both the points $γ x$ in each of the other two copies of $X$ for every $γ \in S$ . This is a kind of bipartite cayley graph, and it’s interesting because perfect matchings in $G (a, S)$ are in bijection with paradoxical decompositions of $X$ (where we promise to only translate the pieces by elements in $S$ ).

In particular, if we want to study definable paradoxical decompositions (say, lebesgue measurable ones), then we can study lebesgue measurable perfect matchings in $G (a, S)$ instead, and we’ve cashed out a tricky problem in geometric group theory for a tricky problem in borel combinatorics. But, at least for me, the combinatorial problem is easier to think about. If you want to hear more about all this, the set of Andrew Marks talks I linked earlier (here it is again) goes into much more detail about all of this. There’s also a wonderful survey by Kechris and Marks.

All in all, it was a fun talk to give! The audience was pretty tired, but I got some good questions, which is always nice. I love descriptive combinatorics, and giving this talk reminded me that I should go and read more about it. I haven’t really thought about this stuff since taking Clinton Conley’s Descriptive Set Theory class…. Almost three years ago now. It’s a shame too, because there’s a lot of really interesting stuff to think about!

As usual, here’s the title and abstract:

Bring Out the Crayons: A Survey of Descriptive Combinatorics

At the interface of topology, logic, and combinatorics, there lies a beautiful source of problems. In today’s talk, I’ll explain what descriptive combinatorics is all about, and survey some results in the area.

The best I have I found in Johnstone’s The Point of Pointless Topology.

Let $X$ be some topological space, and consider $Sh (X)$ , the topos of sheaves on $X$ .

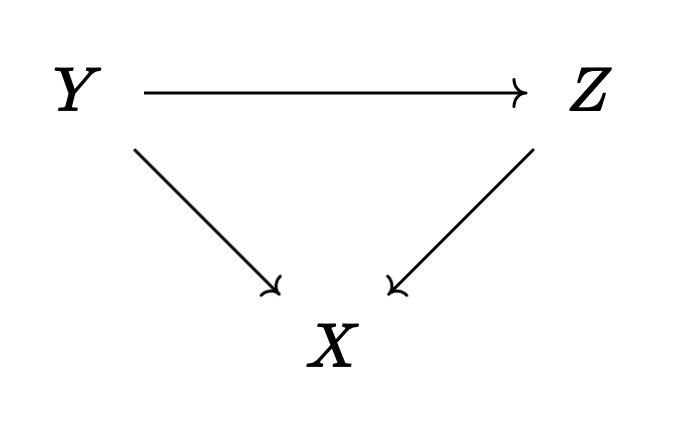
Compact regular locales in $Sh (X)$ correspond to proper maps $Y \to X$ . So any proof about locales that’s constructive (and most are) will go through inside this topos. In particular, the Stone-Čech Compactification for locales tells us that we can embed $Y ↪ Z$ as locales in $Sh (X)$ . But unpacking this means we get a commutative triangle

where our map $Y \to X$ factors (universally) through the proper map $Z \to X$ . ↩
Here “measurable” can mean a few things. Possibly $μ$ -measurable for some measure, but borel-measurable and baire-measurable are two equally common choices. There’s also analytic, etc., but in the talk today I focused on $μ$ , borel, and baire measurability. ↩
I suspect there are other, more precise connections (for instance, to do with the boldface/lightface hierarchies), but I know disappointingly little about these things, so I can’t say for sure. ↩
$R$ , $[0, 1]$ , $(0, 1)$ , $S^{1}$ , and every manifold are polish. Moreover, we have $2^{ω}$ and $ω^{ω}$ , and I think I stopped here. ↩
And can be found in a great paper Brooks’ Theorem for Measurable Colorings by Conley, Marks, and Tucker-Drob. ↩
That I shamelessly stole from here ↩
Shamelessly stolen from wikipedia here, which I feel less bad about. ↩