Topological Categories -- A Unifying Framework

16 Dec 2021 - Tags: featured

I think there is an obvious analogy that most mathematicians notice, perhaps subconsciously, when learning about topological spaces and measure spaces (often within a year or two of each other). The definitions look similar, as do the associated maps (continuous maps pull back open sets to open sets, and measurable maps pull back measurable sets to measurable sets). Seeing this, it’s reasonable to ask if measure spaces and topological spaces share any similarities. More abstractly, one can ask whether their categories share any similarities. The answer turns out to be a resounding yes, and the study of these Topological Categories will be the subject of today’s post!

First, let’s recall some definitions:

A Topology on a set $X$ is a family of subsets of $X$ , called $τ$ , satisfying the following well known axioms:

$\emptyset \in τ$ , $X \in τ$
$τ$ is closed under finite intersections
$τ$ is closed under arbitrary unions

We call the sets $U \in τ$ the Open Sets of the topology¹.

Moreover, let $τ$ be a topology on $X$ and $σ$ a topology on $Y$ . Then a function

f : X \to Y

is called ( $τ$ , $σ$ )-Continuous if and only if

f^{- 1} [U] \in τ

for every $U \in σ$ . When the topologies are clear from context, we simply say $f$ is continuous.

Now let’s notice some superficial observations straight from the definition.

First of all, we have two “obvious” topologies, which are simple in opposite ways. There’s the Discrete Topology where we take $τ_{Δ} = P (X)$ (so every set is open), and there’s the Indiscrete Topology where we take $τ_{\nabla} = {\emptyset, X}$ (so only the sets required in the definition are open).

These are the maximal and minimal topologies it’s possible to put on a set (respectively), and they have some interesting properties:

As a cute exercise, if you haven’t seen them before:

Every function $f : (X, τ_{Δ}) \to (Y, σ)$ is continuous, no matter what $σ$ is.
Every function $g : (Y, σ) \to (X, τ_{\nabla})$ is continuous, no matter what $σ$ is.

Next, you might think that topologies are horribly complicated objects! How do we ever verify that $τ$ is closed under arbitrary unions? How do these show up in nature?

Of course, we almost never actually build topologies by hand. Instead, we give a basis for the topology, where we specify some “basic” sets that we would like to be open, and then formally add in everything else that we need to have. Bases have combinatorial properties which make them nice to work with in practice, but we can actually get by with less!

Again, as a cute exercise, show that if $τ_{α}$ is a family of topologies on $X$ , then $⋂ τ_{α}$ is again a topology.

Since we know $P (X)$ is a complete lattice, and $P (X) = τ_{Δ}$ is itself a topology, we can hit this with some general nonsense from lattice theory²!

The topologies on $X$ form a complete lattice, and every family $T \in P (X)$ has a unique smallest topology containing it

τ_{T} ≜ ⋀ {τ_{α} \supseteq T ∣ τ_{α} is a topology}

In fact, show that this topology $τ_{T}$ is what is traditionally called the topology with subbasis $T$ .

This means we almost never need to build a topology by hand³. Instead, we pick a family of subsets that we want to be open for some reason, then just… look at the topology they generate!

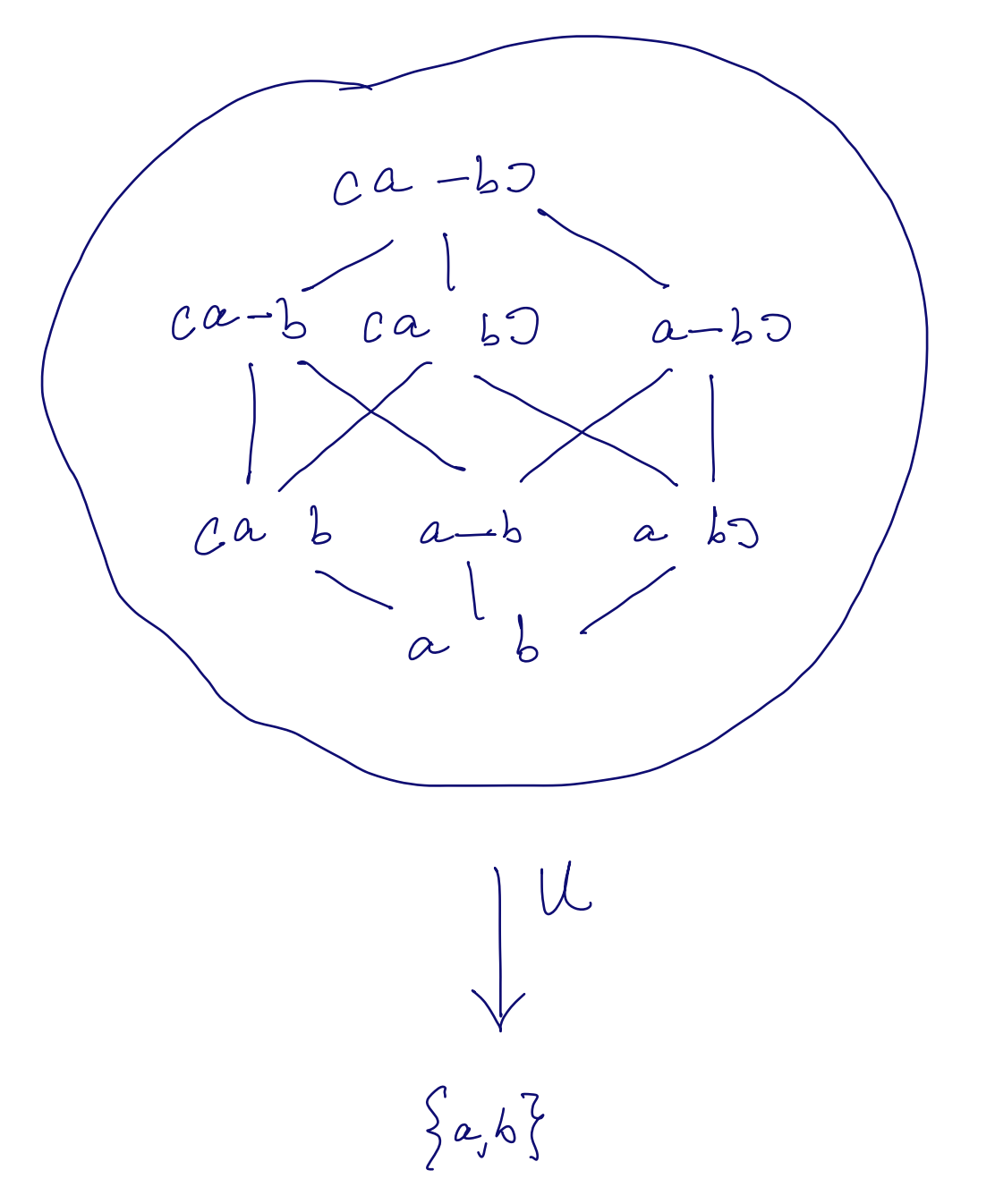
Now, I said earlier that we’re going to be interested in $Top$ , the category of topological spaces. So let’s take a moment to rephrase what we’ve just done in categorical language:

There is a Forgetful Functor

U : Top \to Set

sending $(X, τ)$ to its underlying set $X$ and sending a continuous map $f : (X, τ) \to (Y, σ)$ to the underlying function $f : X \to Y$ .

Moreover, the fibre of $U$ over a set $X$ (that is, the set of all topologies on $X$ ) is a complete lattice, and thus has two distinguished elements: $τ_{Δ}$ and $τ_{\nabla}$ .

The functors $Δ$ and $\nabla : Set \to Top$ sending a set $X$ to the spaces $(X, τ_{Δ})$ and $(X, τ_{\nabla})$ respectively form an adjunction:

$Δ ⊣ U ⊣ \nabla$

This is great, because it means $U$ has to respect all limits and colimits.

We can compute limits/colimits in $Top$ by first computing the limit/colimit of underlying sets, then choosing the smallest (resp. largest) topologies making the limiting arrows continuous⁴.

Show that this is how we actually do define most interesting topological constructions!

For instance, the product topology is defined to have the cartesian product as its underlying set, with the smallest topology making the projection maps continuous. As another example, we define the quotient topology to be the quotient set with the largest topology making the quotient map continuous.

Next we recall

A Measure Algebra on a set $X$ is a family of subsets of $X$ , called $A$ , satisfying the following well known properties:

$\emptyset \in A$ , $X \in A$
$A$ is closed under finite intersections
$A$ is closed under countable unions
$A$ is closed under complementation.

We call the sets $E \in A$ Measurable.

Moreover, if $A$ is a measure algebra on $X$ and $B$ is a measure algebra on $Y$ , then a function

f : X \to Y

is called ( $A$ , $B$ )-Measurable

if and only if

f^{- 1} [E] \in A

for every $E \in B$ . When the measure algebras are clear from context, we simply say $f$ is measurable.

Again, we note the similarities between the definitions of topological spaces and measure spaces, as well as their associated notions of map. Not only that, the similarities in definition beget similarities in structure!

Again, we find two “obvious” measure algebras on $X$ : the Discrete algebra $A_{Δ} = P (X)$ and the Indiscrete algebra $A_{\nabla} = {\emptyset, X}$ .

And again, we find

Every function $f : (X, A_{Δ}) \to (Y, B)$ is measurable
Every function $g : (Y, B) \to (X, A_{\nabla})$ is measurable

Again, these are the maximal and minimal elements of a complete lattice of possible measure algebras on a set $X$ , and again instead of building a measure algebra by hand we almost always have some sets in mind that we want to be measurable. Then we can look at the smallest measure algebra containing those sets and call it a day⁵.

Lastly, we can assemble these into some facts about $Meas$ , the category of measure spaces:

There is a Forgetful Functor

U : Meas \to Set

sending $(X, A)$ to its underlying set $X$ and sending a measurable map $f : (X, A) \to (Y, B)$ to its underlying function $f : X \to Y$ .

Moreover, the fibre of $U$ over a set $X$ (that is, the set of all measure algebras on $X$ ) is a complete lattice, with two distinguished elements $A_{Δ}$ and $A_{\nabla}$ .

The functors $Δ$ and $\nabla : Set \to Meas$ sending a set $X$ to the measure spaces $(X, A_{Δ})$ and $(X, A_{\nabla})$ respectively form an adjunction

$Δ ⊣ U ⊣ \nabla$

And again, this means that $U$ respects all limits and colimits, and that we can compute (co)limits in $Meas$ by computing what the underlying set should be, then “choosing the right measure algebra” $A$ on this (co)limit.

And for our last “again”, show that this really is how we define our interesting constructions on measure spaces! The canonical examples are the product of measure algebras, or the (much less frequently taught⁶) quotient algebra⁷.

Ok, so we’re obviously onto something here. We have some clear parallels between these two categories, and some features which are obviously characteristic of both settings.

The natural thing to do, then, is to abstract these common features into a definition, and see if anything else fits the bill! This lets us more efficiently draw analogies between the different subjects, and (if we’re lucky) will let us unify previously separate theorems. After all, once we prove a theorem using only the abstract properties of these categories, we’ll immediately know that it’s true for $Top$ , $Meas$ , and any other categories we find along the way!

Thankfully, this abstraction has been done for us! You can see the nlab or Adámek, Herrlich, and Strecker’s The Joy of Cats (mainly VI.21) for more details⁸.

Let $U : T \to C$ be a surjective faithful functor that lifts limits uniquely⁹ and has a right adjoint $\nabla$ so that $U \nabla = id$ .

Then $U$ is called a Topological Functor, and we say $T$ is Topological over $C$ .

This definition is nice and minimal in the sense that we have very little to check. Can we compute limits in $T$ by computing limits in $C$ and then lifting? Do indiscrete objects exist? Then we’re golden!

In fact, from this simple definition, lots of results follow. Many of these will look familiar from our motivating examples of $Top$ and $Meas$ . You can find proofs of these in Joy of Cats.

The $U$ -fibre over any object in $C$ is a (possibly large) complete lattice
$U$ has a left adjoint $Δ$ so that $U Δ = id$
$U$ lifts colimits uniquely¹⁰

In fact, we can use these properties to show that as long as $C$ is nice, $T$ must be nice too! Since in practice we often work with categories topological over $Set$ (which is extremely nice), we see that most topologically concrete categories are nice too!

If $C$ is (co)complete, so is $T$
If $C$ is (co)well-powered and $U$ has small fibres¹¹, so is $T$
If $C$ has a (co)generator, so does $T$
If every arrow in $C$ factors as a regepi followed by a mono, then every arrow in $T$ factors in the same way

Notice that the first three of these corollaries conspire to tell us that whenever we can apply the Special Adjoint Functor Theorem to $C$ , we can also do so to $T$ ! This tells us that limit preserving functors out of a topological category almost always have left adjoints, and dually that colimit preserving functors almost always have right adjoints!

There’s also the nice “preservation” properties for topological categories:

A full concrete¹² subcategory $T^{'}$ of $T$ is itself topological over $C$ if and only if it is concretely (co)reflective in $T$

So then, what do topological categories look like?

Here’s the picture which I have in my head¹³. Moreover, when a category I’m interested in looks intuitively like this picture, I always take a second to check if it’s topologically concrete. So far it always has been!

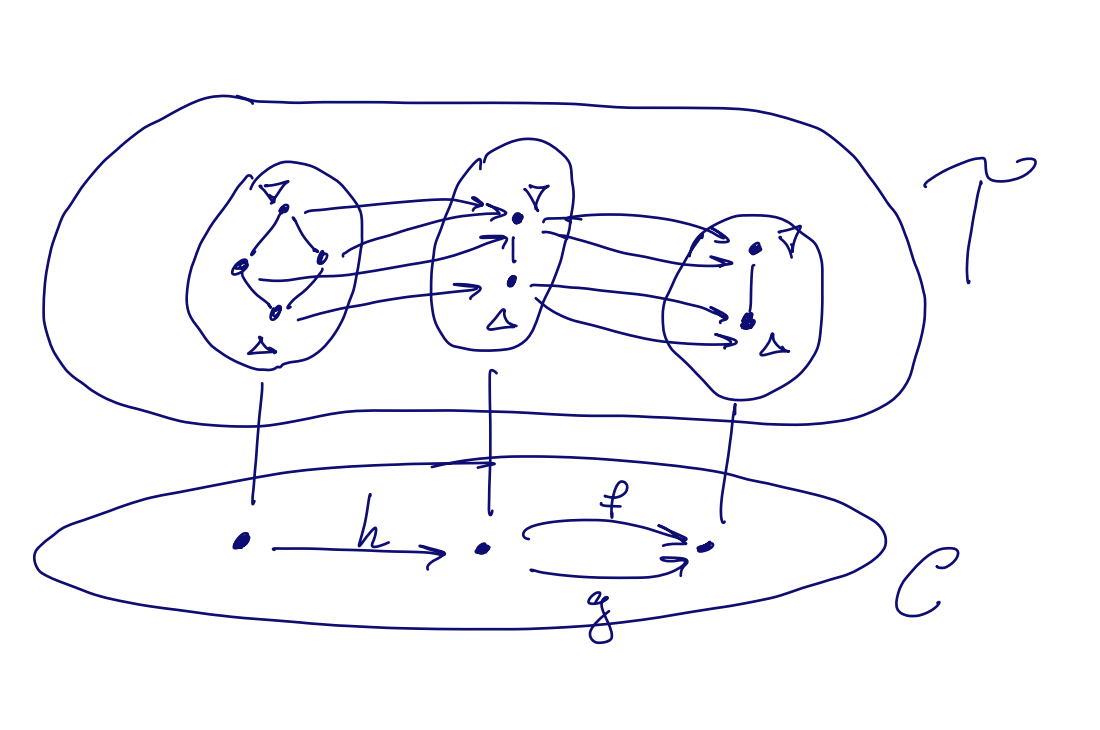
So you see, I’m thinking of topoglogical categories as being fibred over the base category $C$ , with a complete lattice in each fibre. Then the bottom and top elements of the lattice are the discrete and indiscrete structures on a given object of $C$ ¹⁴, and “lifting” a limit corresponds to choosing the correct element of the fibre of the limit as computed downstairs.

Now that we have the machinery of topological categories, we can see that there’s a slew of examples! Off the top of my head, there’s

Graphs

The category $DiGph$ of directed graphs, possibly with self loops. That is, the category whose

objects are $(V, E)$ for $V$ a set and $E \subseteq V \times V$
arrows $f : (V, E) \to (W, F)$ are exactly the functions $f : V \to W$ so that

x E y ⟹ f (x) F f (y)

obviously $U (V, E) = V$

Notice how there’s a complete lattice of graphs¹⁵ (indeed, $P (V \times V)$ ) over every vertex set $V$ . Moreover, there are discrete and indescrte objects (though the indiscrete graph is traditionally called “complete” instead).

Moreover, this gives us lots of other graph categories for free! The following (full) subcategories are all reflective in $DiGph$ , so are topological over $Set$ because $DiGph$ is!

Undirected Graphs (allowing self loops)
Reflexive Graphs (every vertex has a self loop)
Undirected, Reflexive Graphs (obviously)

Notice we cannot get the idea of a graph as most graph theorists understand it. That is, the category of loop free undirected graphs is not topological over $Set$ ! If it were, it would need to be complete, but the category of irreflexive graphs has no terminal object.

Orders

The category $PreOrd$ of preorders (reflexive, transitive relations) with monotone maps is topological over $Set$ .

Next, we notice that the category of sets $V$ equipped with an equivalence relation $\sim$ is topological over $Set$ ! This is because it is a (concretely) reflective subcategory of $PreOrd$ .

Since the category of sets with an equivalence relation is equivalent (indeed, isomorphic) to the category of sets with a partition, we see that partitions are topological too!

⚠ Importantly, $Poset$ is not topological over $Set$ (do you see why?). This is despite the fact that it is a reflective subcategory of $PreOrd$ ! Why is there no contradiction here?

Additionally, given any (possibly large) complete lattice, we can view it as a category in the standard way. A category is topological over the terminal category $1$ if and only if it’s of this form.

Functor Structured Objects

The earlier examples all had objects that looked like $(V, α)$ where $V$ was a set and $α$ was some “relational structure” on $V$ . The arrows in each of these categories are just set theoretic maps that “respect this structure”.

We can now take a vast generalization of all of these, and work with categories of “functor structured objects” each of which will automatically be topological!

Let $T : C \to Set$ be a functor. Following Joy of Cats, we write $Spa (T)$ for the category where

objects are pairs $(C, α)$ where $α \subseteq T (C)$
arrows $(C, α) \to (D, β)$ are $C$ -arrows $C \to D$ so that $(T f) [α] \subseteq β$ .

A category of this form is always concrete over $C$ , and is called Functor Structured

For example, consider the functor $S : Set \to Set$ with $S X = X^{2}$ . Then $DiGph$ is exactly $Spa (S)$ !

Of course, any (co)reflective subcategories of these will also automatically be topological, and it turns out that basically every topological category is of this form! Theorem VI.22.3 in Joy of Cats says¹⁶

$(T, U)$ is fibre-small and topological over $C$ if and only if it is a concretely reflective subcategory of $Spa (T)$ for some $T : C \to Set$ .

Topological Algebras

If you give me some algebriac gadget, like groups, then the category of topological models is probably topological over it.

For instance, $TopGrp$ , the category of topological groups with continuous homomorphisms, is topological over $Grp$ .

This is emblematic of a much more general phenomenon!

Let $(T, U)$ be topological over $C$ . Then actually the functor category $[D, T]$ is topological over $[D, C]$ !

How?

Well, $U \circ - : [D, T] \to [D, C]$ is surjective and faithful. It admits a right adjoint $\nabla \circ -$ , and since limits are computed pointwise in functor categories, we can lift any limits in $[D, C]$ to limits in $[D, T]$ by lifting them pointwise.

Now the same argument works if we focus our attention on those functors which preserve finite products. This is excellent because, following Lawvere, an algebraic structure in $C$ is exactly a finite product preserving functor from a certain “syntactic category” to $C$ !

So then if $T$ is topological over $C$ , we see that (for example) groups in $T$ are topological over groups in $C$ !

A Quick Nonexample

Interestingly, the category of locales is not topological over $Set$ ! This is related to the fact that locales many not have enough points, so what should the forgetful functor be?

Even more interestingly, according to the nlab, the category of spatial locales (that is, those with enough points) is still not topological! Even though it’s equivalent to a reflective subcategory of $Top$ (the full subcategory of sober spaces). This is because the reflector sending a space to its sober-fication is not concrete.

Grothendieck Sites?

This last section is a bit more speculative, because I haven’t checked the details (and probably won’t). But I wanted to include it anyways because it’s what reminded me to make this post at all¹⁷!

Let’s look at the category whose objects are small categories equipped with a grothendieck topology, and whose arrows are functors “respecting the topologies”. See here for more, because (at time of writing) I don’t feel qualified to explain the definition.

We know there is a complete lattice of topologies on a given category $C$ , and moreover that discrete and indiscrete topologies exist. All we need to do, then, is verify the condition about lifting limits, but this seems intuitively clear to me: Take the limit of the underlying categories, and then pick the largest topology on $C$ rendering all the cone maps continuous.

This should mean that the category of sites is topological over $Cat$ , which we might view as a categorification of the fact that $Top$ is topological over $Set$ .

It might be interesting to know if there is some “ $2$ -topological” structure here, but I think I’m not the person to look into that (at least not yet).

That was a long one! But only because there’s so many examples, and I wanted to make sure I motivated the concept too. I’m on vacation now, and might use this time to finish up some posts that I’ve been sitting on for a while (notably the last post in the analysis qual series, on fourier analysis).

I’ve also been thinking some about the mathematics of the Hitomezashi Maker from the last post. There are some interesting questions about what kinds of pictures you get, and unfortunately I’m not enough of a probabilistic combinatorialist to answer most of them! I’ve made some pretty graphs which justify some conjectures, and I’ll probably post about those (and ask on MSE) once I get everything squared away.

Lastly, it’s been almost a year and a half since I’ve written a real piece of music, and I told myself I would write one by the new year. So we might see blog posts slow down a bit (definitely big blog posts like this) while I take some time to be an artist again. I have to write some small pieces to get all the bad music out of me before I write something decent, and I also want to experiment with some electronic music¹⁸. Depending on how proud of the pieces I am, I might post some here.

See you all in the next one ^_^

I’ve been thinking a lot about toposes lately, and these axioms are beginning to take on a new flavor. If we view $τ$ as a poset with $\subseteq$ as the ordering, then it becomes a complete Heyting Algebra (indeed, a Frame). In particular, it’s naturally closed under finite intersections and arbitrary unions, but it also has a “nonstandard” meet operation, which agrees with intersection for finite meets, but is actually defined more generally.

If we view $(τ, \subseteq)$ as a poset category, then we see it is closed under finite limits and arbitrary colimits. However, it’s “accidentally” closed under all limits, though they’re not exactly what you might guess.

This, we see, is entirely analogous to the notion of topos! Toposes have arbitrary colimits and finite limits. Even though they technically admit all limits, these limits don’t behave as nicely. For some more details about this, see this excellent talk by Colin McLarty (Nevertheless, One Should Learn the Language of Topos).

This observation isn’t going to be used at all in the rest of this post, I just needed to say something about it. ↩
Closure operators are ubiquitous in universal algebra and lattice theory, and it’s definitely worth spending some time with them! Basically any book on universal algebra will do, but my first was Burris and Sankappanavar, which is freely (and legally!) available here. Another great resource is Davey and Priestley’s Introduction to Lattices and Order. ↩
Except to torture our new topology students. ↩
Aggravatingly, these are classically called the initial topology (for limits) and the final topology (for colimits), despite the fact that the initial topology is final in the category of cones and the final topology is initial in the category of cocones… 🙃 ↩
Though the construction of this closure operator is much more complicated than the corresponding closure operator for topologies! Indeed every set of $τ_{T}$ is a union of finite intersections of elements of $T$ . But the measurable sets in what is traditionally denoted $σ (T)$ are can be very complicated! See the Borel Hierarchy for more details. ↩
See here, for instance.

Oh well, it seems the terminology has stuck. ↩
Again, the terminology has been all muddled up. Instead of calling the product of measure algebras the “product”, it’s traditional to call it a “tensor product” (see the wikipedia page, for instance), presumably because it’s generated by products of measurable sets in a way that’s analogous to the tensor product of two modules being generated by the pure tensors… ↩
⚠ The definition I give here is actually a theorem in Joy of Cats (VI.21.18). That said, I think it’s a bit simpler to understand than the “classical” definition:

$U$ is topological if and only if every $U$ -structured source has a unique $U$ -initial lift.

Yeah… the language in Joy of Cats takes some getting used to. This is actually a perfectly natural thing to consider, it’s just full of jargon. This nlab article does a pretty good job explaining what this definition “really means”. ↩
This is a kind of “evil” version of creating limits. In fact, this whole definition is evil… We ask for surjectivity rather than essential surjectivity, as well as $U \nabla = id$ rather than just a natural isomorphism.

I’m not sure if anyone has tried to redo Joy of Cats in a way that works up to isomorphism instead of asking for equality on-the-nose in so many places. Thankfully it’s not that big an issue in practice.

I know that Borceux has a definition in his Handbook of Categorical Algebra (Volume 2, definition 7.3.2), but I think it’s still evil… In particular it asks for $U A = B$ on the nose, rather than just $U A ≅ B$ . If anyone knows of efforts to un-evil-ify these definitions, I would love to hear about it! ↩
The fact that our definition only has to do with limits and indiscrete objects, but as a consequence we get the same properties for colimits and discrete objects, is a kind of categorification of the fact that a complete meet-semilattice with a top element is automatically join complete with a bottom element.

In fact, I really feel like topological categories are best understood in terms of the complete lattice living in each fibre. In an earlier draft of this post I tried to make that precise, but ran into some issues. Morally it’s right, but figuring out precisely what conditions you want to put on the lattice was getting tiring and I wanted to get this post out.

The (extremely dedicated) reader can find my attempt in the git history. ↩
This is one of those silly size conditions that we logicians care about. It’s almost always satisfied in practice. For instance, there are only a set worth of topologies, measure spaces, graphs, partitions, etc. on a fixed set $X$ . ↩
Here a Concrete category over $C$ is a category $T$ equipped with a faithful functor $U : T \to C$ .

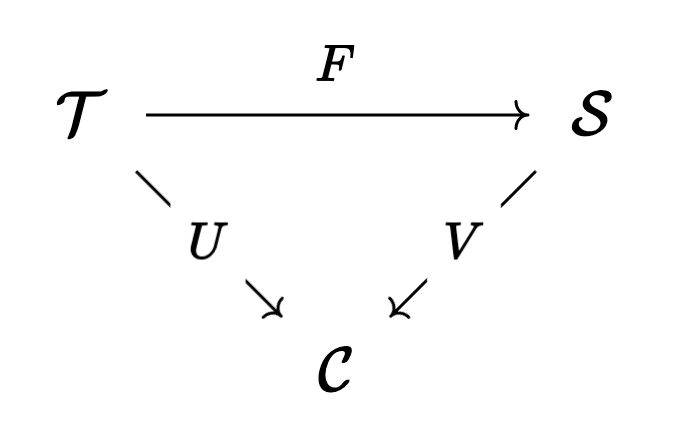
A functor $F$ between concrete categories $(T, U)$ and $(S, V)$ is called concrete when the obvious triangle commutes:

So a concretely (co)reflective subcategory is a subcategory where the inclusion functor is concrete (this means the forgetful functor on the subcategory is the restriction of the forgetful functor on the whole category) whose (co)reflector is also concrete.

It turns out that (co)reflective subcategories often inherit nice properties from their parent category, and they are surprisingly common. One day I’d like to write up a blog post giving some examples and summarizing the nice properties that get preserved, but we’ll see if/when that happens. ↩
Drawn on an ipad for once, instead of on my usual school-sponsored wacom tablet. I’m visiting Remy in New York, and of course he has an ipad because he’s a graphic designer. I left my wacom at home, and it they weren’t so expensive I would consider making the switch. It’s really nice to draw on, haha.

It’s also really hard to justify a purchase like that for something I would use so infrequently, especially now that we’re planning to have fully in person classes again in the winter quarter. ↩
⚠ Keep in mind that this is backwards from the usual set-theoretic order! There the discrete topology is the top element, since every set is open. ↩
Drawing the lattice of directed graphs over a 2 element set is already too big for my taste (it’s a lattice with $16$ elements). But I draw the lattice of undirected graphs over a 2 element set, because I do think it’s worthwhile to think about the picture:

↩
It actually says more than this, and the authors consider “topological axioms” and give lots of examples of how topological categories arise in this way. It’s super interesting, but this post is already getting quite long. ↩
I’ve been planning a post on topological categories for some time, because I really do think they’re an important unifying framework. In fact, it’s the analogy to topological categories that finally got me to understand how grothendieck topologies work. You don’t actually build any. You pick a collection of things that you want to be covering, then say “give me the topology generated by these”. And why can we do that? Because there’s a complete lattice (indeed, a frame!) of topologies on any fixed site. See Borceux’s excellent second lecture from “Toposes at Como” here for more details about this. The whole series is fantastic! ↩
Basically all of my experience is with classical music, but the past two people who commissioned me both wanted something electronic. So even as a career move it’s worth learning, but of course I love electronic music and it would be great to know more about how it works! Also, I’d be lying if I said there isn’t an allure to having a computer make all the sounds for you. It’s much easier than trying to find real live musicians (and pay them) to get your music performed! ↩