Locale Basics
22 May 2022 - Tags: locale-basics
This quarter I’ve been running a reading group for some undergraduates on pointless topology. I want to take some time to write down a summary of the basics of locales (which are the object of study of pointless topology), both so that my students can have a reference for what we’ve covered, and also because I think there’s still space for a really elementary presentation of some of these topics, with a focus on concrete examples.
In particular, it took me a long time to find examples of how people actually build a locale (that doesn’t obviously come from a geometric theory). Hopefully this post will help fill that gap! In the near future, I’d like to write a follow-up post about how we can build new locales from old ones too, but that’s a problem for another day.
Enough build up, though! Let’s get to it ^_^
Our first few weeks were a crash course on the kind of category theory that I usually assume my readers know already, with a focus on partial orders and lattices1. After spending time getting to adjoint functors, we defined a topological space, and then observed that the lattice of open sets has a certain algebraic structure:
- Opens are closed under finite intersection
- Opens are closed under arbitrary union
We quickly abstracted this into a definition2:
A Frame is a lattice
Moreover, we have to explicitly require that
(since lattices are not automatically distributive).
A Homomorphism of Frames is a map
Now, inspired by the fact that continuous maps of topological spaces
Of course, there’s no sense in having a definition without examples!
Geometric Examples
The first important class of examples are the “geometric” ones. Every topological space4 is specified in terms of either a base or a subbase, and we can imitate these constructions exactly in the world of locales.
Let’s do the real numbers to start. These have a basic open for each interval
Now, the intervals
with the convention that
As an easy exercise, draw a picture of two intervals
This is telling us that our open intervals really are a basis in the strong sense that the intersection of two basic opens is basic open.
From here, we want to define a topology by declaring an open set to be an arbitrary union of the basic opens. In the locale-theoretic world, we take this meet-semilattice and (freely) close it under arbitrary joins!
To do that, we recall the adjunction
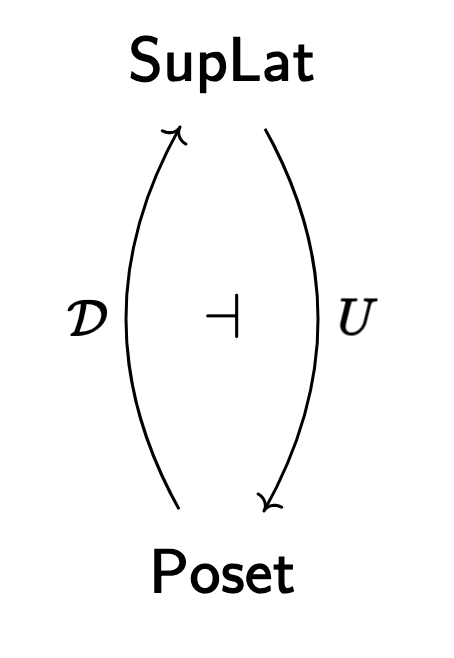
where (as usual)
Then, at the end of the day, we can define the locale
As a nice exercise, you should check that
Of course, there’s nothing special about
Given any meet-semilattice of basic open sets6
Can you modify the construction of
In the next blog post of the series, we’ll talk about product locales,
and we’ll show that
Edit: Thanks to Graham Manuell from the CT Zulip for catching a small bug
here! It’s not enough to take the downset lattice of intervals. We also
need to quotient to make sure
For another example of building locales from a geometric space, let’s
build
In practice, we use the fact that
In particular, the usual topology on
If we need to, though, we can also build
However, it would be nice if we could somehow define
If
Since locales are dual to frames, a quotient locale (that is, an
epimorphism) should correspond to a subframe (that is, a monomorphism),
and a moment’s meditation on the quotient topology shows that
we want to consider the sublocale of open sets fixed by the
Intuitively, we’re identifying an open set of
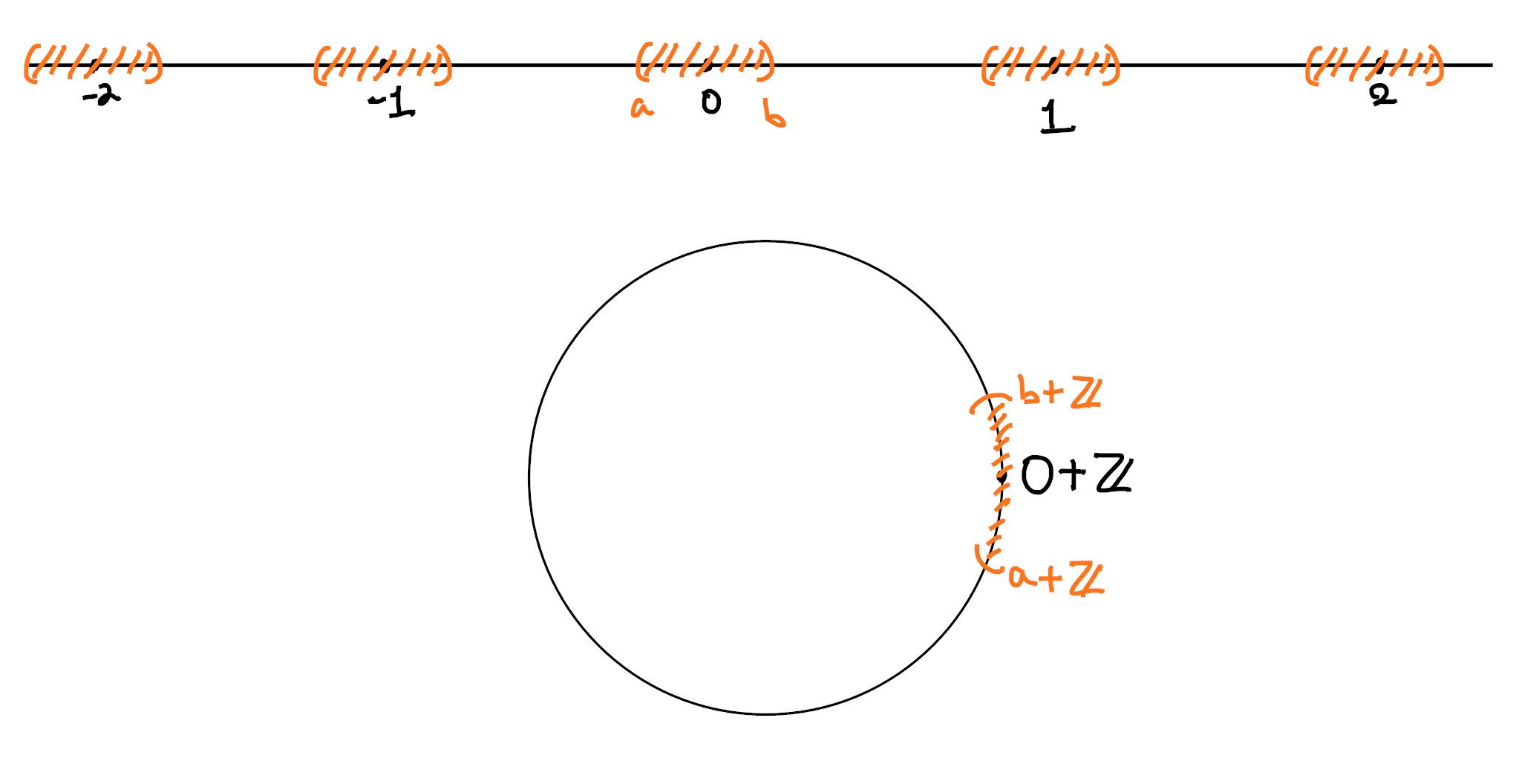
But what, I hear you asking, if our basic opens are just basic in the usual sense? For instance, how can we describe a locale associated to a general metric space?
The answer, dear reader, is Sites8.
Johnstone (in section II.2.11 of Stone Spaces) requires his sites to be meet semilattices, but this is still not as general as I would like9. After all, the open balls in a metric space are very rarely closed under intersection! It took me a surprisingly long time to find a satisfying construction, but Vickers (in Compactness in Locales and in Formal Topology) gives the following definition, which does exactly what I want:
A Flat Site is a preorder
If
We think of the relation
Then the frame presented by a flat site is
That is, we we force the coverage relation
Build a frame associated to a metric space
This might feel slightly tautologous, since metric spaces are hausdorff, thus their usual topology already gives us a frame.
Logical Examples
Of course, locale theory (like most of my interests) has a dual nature as a geometirc subject and a logical subject. The previous section was about locales which arise from geometric objects, but what about locales arising logically?
Let’s start with the notion of a (propositional) geometric theory.
Fix a family of “primitive propositions”
Next, a geometric sequent is an object of the form
where
Finally, a geometric theory is a set
There is a sequent calculus for geometric logic, which, for those in the
know, is exactly what you expect11. All that we need to know is that it lets
us derive the truth of certain sequents in a way that formally mirrors the
way we prove things as mathematicians. For instance, one can derive the sequent
This is important because the language12
If we then quotient by the equivalence relation of
Now, given a theory
for each
This is again a frame, which we should think of as the formulas in
This was all very abstract, so let’s see some concrete examples:
Let
What’s the use of this theory? Well recall a (classical) model of a
(propositional) theory
Now, a model of this theory assigns each
Through this lens, the first two axioms express that for every
So (classical) models of
We can push this further, though!
Consider a theory
To get some practice interpreting geometric theories, you should try to figure out what a (classical) model of this theory looks like.
As before, the first two axioms assert that a model should define a
function
Do you see why this is a nontrivial theory with no classical models?
The locales
Then a (classical) model of this theory is exactly the graph
of a norm-decreasing linear functional on
Now, we’ve said that this is a very flexible appraoch for building locales… but just how flexible is it?
Well, it turns out that every locale arises in this way!
That is, for each locale
As our primitive propositions, we’ll take the elements
Now, tautologically, it’s clear that the lindenbaum algebra for this theory
is
Points
You’ve probably heard locale theory referred to as “pointless topology” (especially since I called it that at the start of the post!). But what does that mean?
Well, in topological spaces, we can identify points of
Then we perform a tried and true maneuver, used by mathematicians everywhere:
we take a theorem in the old setting, and turn it into a definition in our
new setting! So for us, a Point of a locale
If it’s not obvious, you should take a moment to think about why the one point
space
Now we get to one of the most important punchlines in locale theory!
If you recall, the lattice
But turning the arrows around, we see that (classical) models of
In this way, we can view
One way to see that this nontrivial structure is interesting is by
considering more general kinds of point. For instance, instead of assigning
each primitive proposition the value
Again, though, we dualize, and for a locale
So now we have two different ways of thinking about a continuous map
But logically, we know that we can think of these as
The answer is “yes”!
For each point
But there’s another, third way of viewing a map
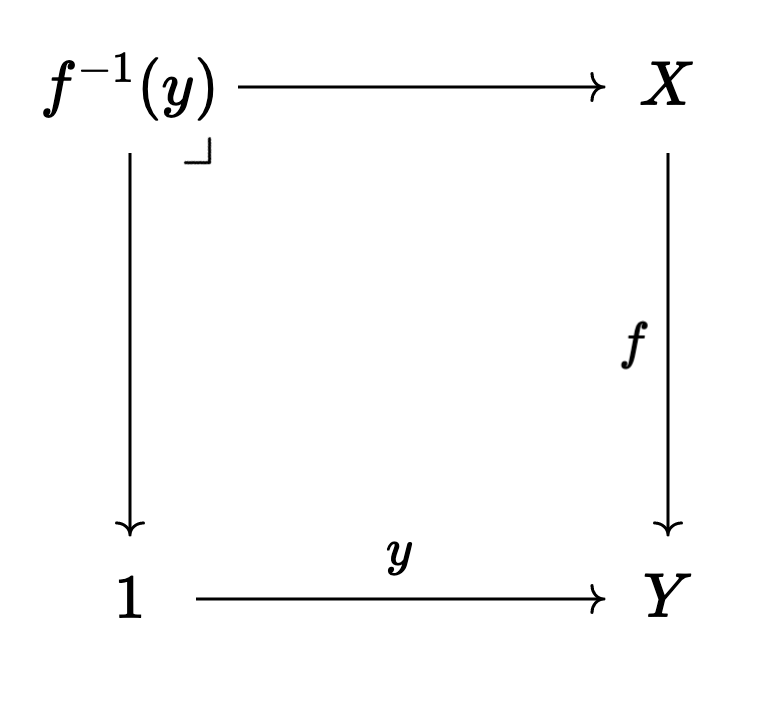
here
Ok, this was a long one, but I think there’s a lot to say about frames and locales. I’m surprised how difficult it is to find concrete examples of certain calculations on frames, and ways of building them (though maybe I’m just not sure where to look). Either way, I hope my students find this a useful (if somewhat fleshed out) review of the localic material we’ve covered so far, and I hope that future readers find this an approachable introduction to the basics of locale theory.
Take care, everyone, and I’ll see you soon ^_^
PS: I’ve been reading a lot of locale theory lately, particularly while looking for references that showcase either explicit constructions or interesting use cases. I usually include references either in the text or in footnotes, but I’ll actually include a short bibliography here for the papers that I found particularly insightful:
- Anel, Mathieu, and André Joyal. “Topo-Logie.” In New Spaces in Mathematics, edited by Mathieu Anel and Gabriel Catren, 1st ed., 155–257. Cambridge University Press, 2021. https://doi.org/10.1017/9781108854429.007.
- Banaschewski, Bernhard, and Christopher J. Mulvey. “A Constructive Proof of the Stone-Weierstrass Theorem.” Journal of Pure and Applied Algebra 116, no. 1 (March 28, 1997): 25–40. https://doi.org/10.1016/S0022-4049(96)00160-0.
- ———. “A Globalisation of the Gelfand Duality Theorem.” Annals of Pure and Applied Logic 137, no. 1 (January 1, 2006): 62–103. https://doi.org/10.1016/j.apal.2005.05.018.
- Blechschmidt, Ingo. “Generalized Spaces for Constructive Algebra.” ArXiv:2012.13850 [Math], December 26, 2020. http://arxiv.org/abs/2012.13850.
- Borceux, Francis. Categories of Sheaves. Digitally printed version. Handbook of Categorical Algebra / Francis Borceux 3. Cambridge: Cambridge Univ. Press, 2008.
- Chen, Xiangdong. “On Binary Coproducts of Frames,” n.d., 14.
- Day, B. J. “Locale Geometry.” Pacific Journal of Mathematics 83, no. 2 (August 1, 1979): 333–39. https://doi.org/10.2140/pjm.1979.83.333.
- He, Wei, and MaoKang Luo. “Completely Regular Proper Reflection of Locales over a given Locale.” Proceedings of the American Mathematical Society 141, no. 2 (June 5, 2012): 403–8. https://doi.org/10.1090/S0002-9939-2012-11329-2.
- Isbell, John. “Product Spaces in Locales.” Proceedings of the American Mathematical Society 81, no. 1 (1981): 116–18. https://doi.org/10.2307/2044000.
- ———. “Atomless Parts of Spaces.” MATHEMATICA SCANDINAVICA 31 (June 1, 1972): 5. https://doi.org/10.7146/math.scand.a-11409.
- Johnstone, Peter T. Stone Spaces. Paperback ed., Repr. Cambridge Studies in Advanced Mathematics 3. Cambridge: Cambridge Univ. Press, 1992.
- Pelletier, Joan Wick. “Locales in Functional Analysis.” Journal of Pure and Applied Algebra 70, no. 1 (March 15, 1991): 133–45. https://doi.org/10.1016/0022-4049(91)90013-R.
- Picado, Jorge, and Aleš Pultr. Frames and Locales: Topology without Points. Frontiers in Mathematics. Basel: Birkhäuser, 2012.
- ———. “Notes on the Product of Locales.” Mathematica Slovaca 65, no. 2 (April 1, 2015): 247–64. https://doi.org/10.1515/ms-2015-0020.
- Vickers, Steven. “Geometric Logic in Computer Science.” In Theory and Formal Methods 1993, edited by Geoffrey Burn, Simon Gay, and Mark Ryan, 37–54. Workshops in Computing. London: Springer London, 1993. https://doi.org/10.1007/978-1-4471-3503-6_4.
- ———. “Compactness in Locales and in Formal Topology.” Annals of Pure and Applied Logic 137, no. 1–3 (January 2006): 413–38. https://doi.org/10.1016/j.apal.2005.05.028.
- ———. “Continuity and Geometric Logic.” Journal of Applied Logic, Logic Categories Semantics, 12, no. 1 (March 1, 2014): 14–27. https://doi.org/10.1016/j.jal.2013.07.004.
-
I feel like this is particularly economical for a few reasons:
First, posets and lattices are simple combinatorial objects that you can understand without much background in abstract algebra or topology. We also get two “levels” of categories out of this, since every poset is a category in its own right, but we can also consider the category of posets, or any one of the zoo of categories of lattices.
In fact, the zoo of lattice categories is nice, because it forces you to acknowledge that it’s the arrows that matter. After all, frames (which we’ll define soon) and complete heyting algebras are the same thing! We can only distinguish between the categories because the homomorphisms are different.
This means that we can see categorical constructions in multiple lights very quickly: Products in a poset are meets, while products in the category of posets are given by a poset of tuples. Adjoint functors between posets are galois connections, while adjoint functors between the categories of posets and meet semilattices might be a free/forgetful pair, etc. ↩
-
The definition given on the nlab is nice because it make the analogy with topoi incredibly clear. It’s an easy exercise that our definitions are equivalent. ↩
-
As a nice exercise:
Show that every frame is also a Heyting Algebra. You can do this with abstract nonsense (use the adjoint functor theorem) or directly (give an explicit expression for the arrow
You should do whichever comes less naturally to you (or both, if neither comes naturally).
As a part 2, you should show that defining frames to be complete heyting algebras is incorrect, since morphisms of heyting algebras should preserve
(You can see this mathoverflow question if you need a hint) ↩
-
That I can think of right now ↩
-
There’s actually a lot to say about this construction! It turns out that
Then
Again, there’s a lot to say here, since frames/locales are analogous in many was to grothendieck topoi, and this method of getting a locale by looking at “presheaf posets” is one instance of that analogy! ↩
-
Notice that we’re assuming the intersection of two basic opens is itself basic open. The usual definition is that the intersection of two basic opens merely contains a basic open – this seems like a property that should have a name, but I don’t know of one. Hopefully someone can leave a comment clarifying this ^_^
Either way, we’ll relax this assumption later on in the post! ↩
-
Which I’d like to prove in its own blog post… hopefully a shorter one, since the proof really isn’t that bad.
For the impatient reader (or if I never get to it) you can find a proof in Johnstone’s Stone Spaces, section II.1.7 ↩
-
This is yet another analogy to topos theory. See here for more ↩
-
Though it does make the construction go slightly more smoothly. This, again, is analogous to the setting of sites on a category in topos theory, where assuming your category has pullbacks makes the construction a bit simpler. ↩
-
Notice this quotient is taken in the category of suplattices, so it’s not obvious that we should actually get a frame out the other side.
This is where the flat stability axiom comes into play, since it tells us (roughly) that we can “pull back” a cover
For a full proof, see theorem 5 in Vickers’ Compactness in Locales and in Formal Topology ↩
-
We have the usual structural rules, and all the connectives work in the traditional way, with the rules for infinite disjunction being the natural generalization of the usual disjunction rules. We won’t need to know the intricacies of the system here, so I’ll omit a full description, but the interested reader can find one in section D1.3 of the elephant. ↩
-
That is, the set of geometric formulas with the given primitive propositions ↩
-
So, for instance, given two equivalence classes of formulas
Similarly, for (infinitary) joins and disjunction.
This is why we need to quotient by provable equivalence, because
-
You’ll often hear logicians talk about formulas “up to
This is what we’re talking about! ↩
-
See, for instance, Pelletier’s excellent survey Locales in Functional Analysis. ↩
-
Though this sounds much more exciting than it is… Prepare to be underwhelmed :P ↩
-
In the same way that propositional geometric theories all have a classifying locale, more general predicate geometric theories admit a classifying topos!
Since every algebraic theory is geometric, this tells us that there’s a topos
This also plays nicely with the intution that
-
And this is one of the big reasons to favor locales over topological spaces! Locales behave much better under this interpretation, basically because their theorems are provable constructively. Since the slice category of locales over