Locale Basics

22 May 2022 - Tags: locale-basics

This quarter I’ve been running a reading group for some undergraduates on pointless topology. I want to take some time to write down a summary of the basics of locales (which are the object of study of pointless topology), both so that my students can have a reference for what we’ve covered, and also because I think there’s still space for a really elementary presentation of some of these topics, with a focus on concrete examples.

In particular, it took me a long time to find examples of how people actually build a locale (that doesn’t obviously come from a geometric theory). Hopefully this post will help fill that gap! In the near future, I’d like to write a follow-up post about how we can build new locales from old ones too, but that’s a problem for another day.

Enough build up, though! Let’s get to it ^_^

Our first few weeks were a crash course on the kind of category theory that I usually assume my readers know already, with a focus on partial orders and lattices¹. After spending time getting to adjoint functors, we defined a topological space, and then observed that the lattice of open sets has a certain algebraic structure:

Opens are closed under finite intersection
Opens are closed under arbitrary union

We quickly abstracted this into a definition²:

A Frame is a lattice $(F, 0, 1, \land, \lor)$ which is closed under arbitrary joins, which we write as $⋁ a_{α}$ .

Moreover, we have to explicitly require that

a \land (⋁ b_{α}) = ⋁ (a \land b_{α})

(since lattices are not automatically distributive).

A Homomorphism of Frames is a map $φ : F \to G$ which preserves finite meets and arbitrary joins³.

Now, inspired by the fact that continuous maps of topological spaces $(X, τ) \to (Y, σ)$ are in bijection with frame homomorphisms from $σ \to τ$ , we define the category of Locales to be opposite the category of frames.

Of course, there’s no sense in having a definition without examples!

Geometric Examples

The first important class of examples are the “geometric” ones. Every topological space⁴ is specified in terms of either a base or a subbase, and we can imitate these constructions exactly in the world of locales.

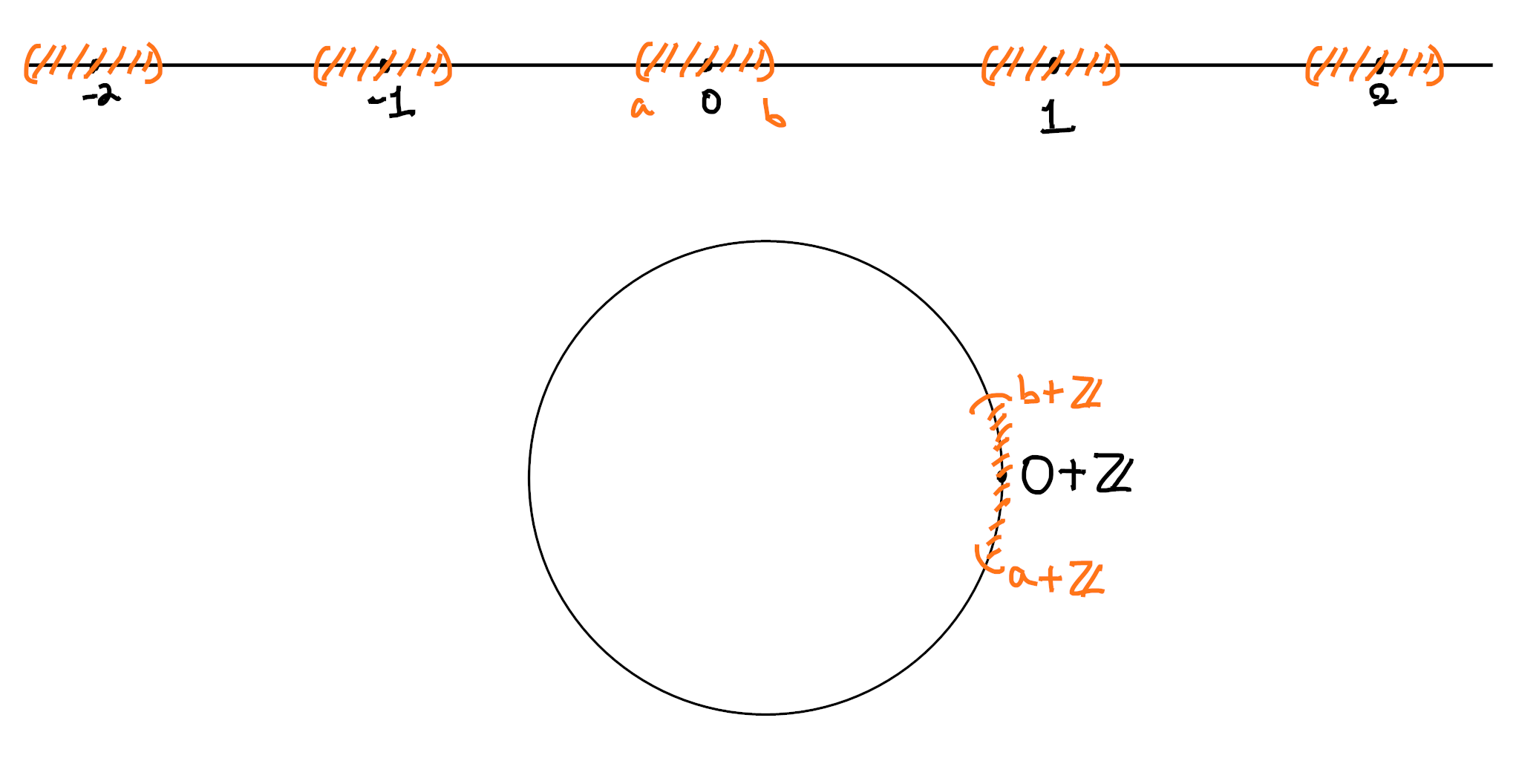
Let’s do the real numbers to start. These have a basic open for each interval $(a, b)$ . Classically we can take all such intervals, but constructively it’s more hygienic to take only the intervals with rational endpoints. Obviously these generate the same topology, so we’re not losing anything by doing this.

Now, the intervals $(a, b)$ form a meet semilattice where we define

(a, b) \land (a^{'}, b^{'}) = (max (a, a^{'}), min (b, b^{'}))

with the convention that $(a, b) = ⊥$ whenever $b < a$ .

As an easy exercise, draw a picture of two intervals $(a, b)$ and $(a^{'}, b^{'})$ and convince yourself that their intersection is really given by the meet as defined above

This is telling us that our open intervals really are a basis in the strong sense that the intersection of two basic opens is basic open.

From here, we want to define a topology by declaring an open set to be an arbitrary union of the basic opens. In the locale-theoretic world, we take this meet-semilattice and (freely) close it under arbitrary joins!

To do that, we recall the adjunction

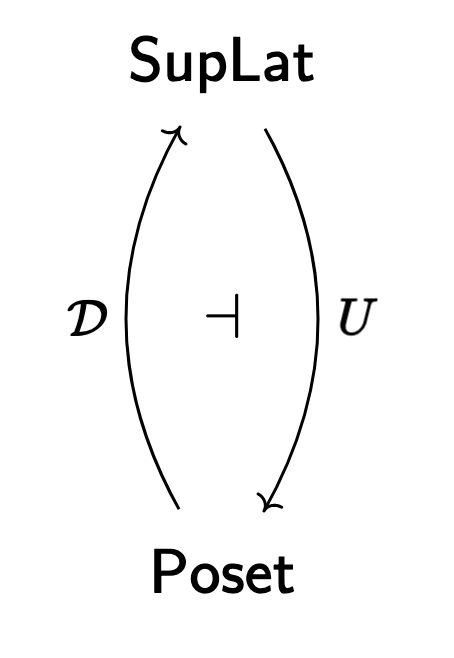
where (as usual) $U$ is the forgetful functor and $D$ is the downset functor, which sends a poset $P$ to the free (sup)lattice $D P$ whose elements are the downwards-closed subsets of $P$ ⁵. The unit of this adjunction sends $p \in P$ to $↓ p = {x \in P ∣ x \leq p}$ .

Then, at the end of the day, we can define the locale $R$ to be generated by the basic opens $(a, b)$ with $a < b \in Q$ . These assemble into a meet-semilattice $P$ , and the downset lattice $D P$ is a frame.

As a nice exercise, you should check that $D P$ really is a frame. Moreover, that the inclusion $P ↪ D P$ preserves $\land$ .

Of course, there’s nothing special about $R$ here!

Given any meet-semilattice of basic open sets⁶ $(M, \land)$ , the downsets $D M$ form a locale where every open is the union of basic opens in $m$ (here, as usual, we identify $m \in M$ with the principal downset $↓ m \in D M$ ).

Can you modify the construction of $R$ to build a locale for $R^{2}$ , or more generally $R^{n}$ ?

In the next blog post of the series, we’ll talk about product locales, and we’ll show that $R \times R ≅ R^{2}$ .

Edit: Thanks to Graham Manuell from the CT Zulip for catching a small bug here! It’s not enough to take the downset lattice of intervals. We also need to quotient to make sure $\underset{n}{⋁} (a + \frac{1}{n}, b - \frac{1}{n}) = (a, b)$ , for instance. More generally we say that the join of all intervals contained in $(a, b)$ should be $(a, b)$ itself. This is actually a special case of a Coverage, which we’ll discuss more later on!

For another example of building locales from a geometric space, let’s build $S^{1}$ together! We have a few options for how to do this.

In practice, we use the fact that $S^{1}$ as a topological space is hausdorff, thus sober. Then we appeal to an important theorem⁷ that the full subcategory of sober topological spaces is equivalent to the full subcategory of “spatial locales”.

In particular, the usual topology on $S^{1}$ , viewed as a frame, gives a locale for $S^{1}$ with no changes necessary.

If we need to, though, we can also build $S^{1}$ by hand. After all, we can describe the open arcs and their intersections as basic opens, then take downsets just as we did for $R$ .

However, it would be nice if we could somehow define $S^{1}$ to be $R / Z$ . I’ve never actually seen anybody talk about how to do this, so this blog post seems like a perfect place!

If $Z$ is acting on $R$ by translation, that means we have an action of $Z$ on the frame of opens of $R$ , where a basic open $(p, q)$ pulls back to the basic open $(p - 1, q - 1)$ .

Since locales are dual to frames, a quotient locale (that is, an epimorphism) should correspond to a subframe (that is, a monomorphism), and a moment’s meditation on the quotient topology shows that we want to consider the sublocale of open sets fixed by the $Z$ action. So a typical open in this sublocale looks like

\underset{n \in Z}{⋁} (p - n, q - n)

Intuitively, we’re identifying an open set of $S^{1}$ with its preimage in $R$ , which lets us identify the frame of opens of $S^{1}$ with a subframe of the opens of $R$ .

But what, I hear you asking, if our basic opens are just basic in the usual sense? For instance, how can we describe a locale associated to a general metric space?

The answer, dear reader, is Sites⁸.

Johnstone (in section II.2.11 of Stone Spaces) requires his sites to be meet semilattices, but this is still not as general as I would like⁹. After all, the open balls in a metric space are very rarely closed under intersection! It took me a surprisingly long time to find a satisfying construction, but Vickers (in Compactness in Locales and in Formal Topology) gives the following definition, which does exactly what I want:

A Flat Site is a preorder $(P, \leq)$ equipped with a coverage relation $⊲$ between $P$ and the powerset $P (P)$ which satisfies the following “flat stability” axiom:

If $p ⊲ A$ and $q \leq p$ , there should be a $B \subseteq (↓ q) \cap (↓ A)$ so that $q ⊲ B$ .

We think of the relation $p ⊲ A$ as saying that “ $A$ covers $p$ ”

Then the frame presented by a flat site is

D P / p \leq ⋁ A (for every p ⊲ A)

That is, we we force the coverage relation $p ⊲ A$ to become an actual covering in the frame¹⁰.

Build a frame associated to a metric space $(X, d)$ by constructing a flat site associated to $X$ .

This might feel slightly tautologous, since metric spaces are hausdorff, thus their usual topology already gives us a frame.

Logical Examples

Of course, locale theory (like most of my interests) has a dual nature as a geometirc subject and a logical subject. The previous section was about locales which arise from geometric objects, but what about locales arising logically?

Let’s start with the notion of a (propositional) geometric theory.

Fix a family of “primitive propositions” $P_{α}$ . Then geometric formulas are described by the following grammar:

\begin{aligned} φ ::= & P_{α} \\ | ⊤ \\ | ⊥ \\ | φ \land ψ \\ | φ \lor ψ \\ | ⋁ φ_{α} \end{aligned}

Next, a geometric sequent is an object of the form

φ_{1}, \dots, φ_{n} ⊢ ψ

where $φ$ and $ψ$ are geometric formulas. We interpret this as expressing “whenever all of the $φ_{k}$ are true, $ψ$ is true too”.

Finally, a geometric theory is a set $T$ of geometric sequents, which we think of as axioms for $T$ .

There is a sequent calculus for geometric logic, which, for those in the know, is exactly what you expect¹¹. All that we need to know is that it lets us derive the truth of certain sequents in a way that formally mirrors the way we prove things as mathematicians. For instance, one can derive the sequent $φ \land ψ ⊢ ψ \land φ$ , which tells us that $\land$ is commutative.

This is important because the language¹² $L ({P_{α}})$ is a preorder if we define $φ \leq ψ$ by $φ ⊢ ψ$ . Intuitively, elements “higher up the poset” are “more true”, with $⊤$ and $⊥$ as the top and bottom elements.

If we then quotient by the equivalence relation of $x \leq y \leq x$ (so we consider two provably-equivalent formulas to be “the same”) then we get a frame, where the lattice operations are given by the logical ones¹³! In fact, this construction gives the free frame generated by the set $P_{α}$ of primitive propositions.

Now, given a theory $T$ with primitive propositions $P_{α}$ , we define the Lindenbaum Algebra $L [T]$ to be the frame of formulas in $P_{α}$ modulo the relations

φ_{1}, \dots, φ_{n} \leq ψ

for each $(φ_{1} \dots, φ_{n} ⊢ ψ) \in T$ .

This is again a frame, which we should think of as the formulas in $L ({P_{α}})$ up to provable equivalence, where now we may use the sequents in $T$ as axioms in our proofs¹⁴! In the case we view this frame as a locale, we call it the Classifying Locale of $T$ .

This was all very abstract, so let’s see some concrete examples:

Let $X$ be a set, and consider a theory $T$ with one primitive proposition $σ_{x, y}$ for each $x, y \in X$ , and axioms

\begin{aligned} ⊤ & ⊢ \underset{y \in X}{⋁} σ_{x, y} & (for each x \in X) \\ σ_{x, y}, σ_{x, z} & ⊢ ⊥ & (for y \neq z \in X) \\ σ_{x, y} & ⊢ σ_{y, x} \end{aligned}

What’s the use of this theory? Well recall a (classical) model of a (propositional) theory $T$ is exactly a frame homomorphism $L [T] \to {⊥, ⊤}$ .

Now, a model of this theory assigns each $σ_{x, y}$ to $⊥$ or $⊤$ , thus a model is really picking out a subset of $X \times X$ – namely those pairs $(x, y)$ so that $σ_{x, y} = ⊤$ .

Through this lens, the first two axioms express that for every $x$ , there is exactly one $y$ with $σ_{x, y} = ⊤$ , so that our model is naming a function (which I’ll call $f_{σ} : X \to X$ ). The last axiom is asserting that $f_{σ} (x) = y$ implies $f_{σ} (y) = x$ . That is, $f_{σ}$ should be an involution!

So (classical) models of $T$ are exactly $Z / 2$ actions on $X$ .

We can push this further, though!

Consider a theory $T$ with primitive propositions $θ_{n, x}$ for $n \in N$ and $x \in R$ , and the axioms

\begin{aligned} ⊤ & ⊢ \underset{x \in R}{⋁} θ_{n, x} & (for each n \in N) \\ θ_{n, x}, θ_{n, y} & ⊢ ⊥ & (for x \neq y \in R) \\ ⊤ & ⊢ \underset{n \in N}{⋁} θ_{n, x} & (for each x \in R) \end{aligned}

To get some practice interpreting geometric theories, you should try to figure out what a (classical) model of this theory looks like.

As before, the first two axioms assert that a model should define a function $f_{θ} : N \to R$ . But what does the third axiom assert?

Do you see why this is a nontrivial theory with no classical models?

The locales $L [T]$ are surprisingly flexible. For instance, say $B$ is a seminormed space. Then we can describe its (localic) dual space by considering a geometric theory with primitive propositions “ $φ (a) \in (r, s)$ ” for each $a \in B$ , $r, s \in Q$ . These should satisfy axioms:

\begin{aligned} ⊤ & ⊢ φ (0) \in (r, s) & (for r < 0 < s) \\ φ (0) \in (r, s) & ⊢ ⊥ & (otherwise) \\ φ (a) \in (r, s) & ⊢ φ (- a) \in (- s, - r) \\ φ (a) \in (r, s) & ⊢ φ (t a) \in (t r, t s) & (for t > 0 \in Q) \\ φ (a) \in (r, s), φ (a^{'}) \in (r^{'}, s^{'}) & ⊢ φ (a + a^{'}) \in (r + r^{'}, s + s^{'}) \\ φ (a) \in (r, s) & ⊢ φ (a) \in (r, s^{'}) \lor φ (a) \in (r^{'}, s) & (whenever r < r^{'} < s^{'} < s) \\ ⊤ & ⊢ φ (a) \in (- 1, 1) & (whenever ‖ a ‖ < 1) \\ φ (a) \in (r, s) & ⊢ \underset{r < r^{'} < s^{'} < s}{⋁} φ (a) \in (r^{'}, s^{'}) \\ \underset{r < r^{'} < s^{'} < s}{⋁} φ (a) \in (r^{'}, s^{'}) & ⊢ φ (a) \in (r, s) \end{aligned}

Then a (classical) model of this theory is exactly the graph of a norm-decreasing linear functional on $B$ ! Moreover, if we use this formulation of the dual space of $B$ , we can get a completely constructive proof of the Hahn-Banach theorem¹⁵!

Now, we’ve said that this is a very flexible appraoch for building locales… but just how flexible is it?

Well, it turns out that every locale arises in this way! That is, for each locale $L$ , there is a geometric theory which it classifies¹⁶.

As our primitive propositions, we’ll take the elements $U_{α} \in L$ (viewed as a frame). Then our theory will be exactly the “cayley table” of $L$ . As axioms, we’ll take $U_{1} \land U_{2} ⊢ U_{3}$ whenever $U_{3}$ is the meet of $U_{1}$ and $U_{2}$ in $L$ . Similarly, we’ll add axioms saying that $⋁ U_{α} ⊢ U^{*}$ whenever $U^{*}$ really is the join of the $U_{α}$ as computed in $L$ .

Now, tautologically, it’s clear that the lindenbaum algebra for this theory is $L$ , as desired.

Points

You’ve probably heard locale theory referred to as “pointless topology” (especially since I called it that at the start of the post!). But what does that mean?

Well, in topological spaces, we can identify points of $X$ with maps ${⋆} \to X$ , since these maps are completely determined by the point $f (⋆) \in X$ (and conversely, every point determines a map).

Then we perform a tried and true maneuver, used by mathematicians everywhere: we take a theorem in the old setting, and turn it into a definition in our new setting! So for us, a Point of a locale $L$ is a continuous map $1 \to L$ , where $1$ , the terminal locale, is the one point space (that is, the locale whose frame of opens is ${⊥, ⊤}$ )

If it’s not obvious, you should take a moment to think about why the one point space ${⋆}$ in topology corresponds to the locale whose frame of opens is ${⊥, ⊤}$ .

Now we get to one of the most important punchlines in locale theory!

If you recall, the lattice ${⊥, ⊤}$ showed up before too… We saw that frame homomorphisms $L [T] \to {⊥, ⊤}$ were exactly classical models of the theory $T$ !

But turning the arrows around, we see that (classical) models of $T$ are nothing but points of $L [T]$ !

In this way, we can view $L [T]$ as the “space of models” of $T$ . Of course, some theories don’t have any classical models: for instance, the theory of surjections $N \to R$ that we built earlier. In this case, our locale has no points! But nonetheless it has nontrivial topological structure.

One way to see that this nontrivial structure is interesting is by considering more general kinds of point. For instance, instead of assigning each primitive proposition the value $⊥$ or $⊤$ , you might assign them values in some other frame $F$ . These “ $F$ -valued models” are interesting already, but they really shine when we see the analogue in topos theory¹⁷.

Again, though, we dualize, and for a locale $X$ we say that the “ $X$ -valued points of $L$ ” (equivalently the $X$ -valued models of $T$ ) are exactly the continuous maps $X \to L$ (equivalently $X \to L [T]$ ).

So now we have two different ways of thinking about a continuous map $f : X \to Y$ . The first way is just what it is: a continuous map.

But logically, we know that we can think of these as $T$ models in a world with more than two truth values. Is there some geometric interpretation of this idea?

The answer is “yes”!

For each point $p : 1 \to X$ , we get a map $f p : 1 \to Y$ . So then we might think of $f$ as giving us points in $Y$ which vary continuously in $X$ . That is, “points” $p_{x}$ of $Y$ which continuously depend on a parameter from $x$ . This seems like a kind of silly thing to do, but it turns out to be a very useful way of thinking.

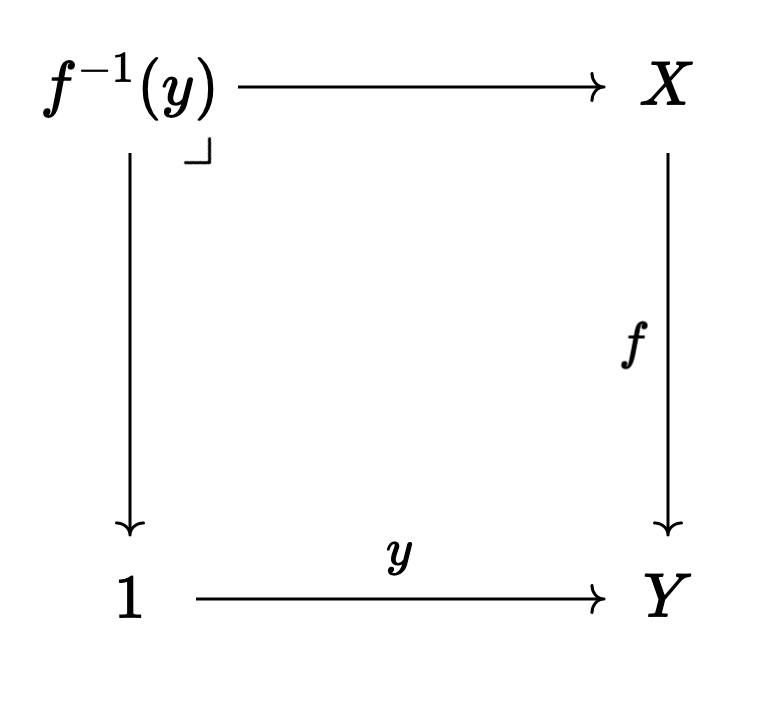
But there’s another, third way of viewing a map $f : X \to Y$ – namely as a bundle. For each point $y$ of $Y$ we get a pullback

here $X_{y} = f^{- 1} (y)$ is a locale (since the category of locales is complete), and we think of $X$ as being a family of locales $X_{y}$ which varies continuously in $Y$ . This is another very fruitful idea which I’ll probably talk about in a future blog post¹⁸.

Ok, this was a long one, but I think there’s a lot to say about frames and locales. I’m surprised how difficult it is to find concrete examples of certain calculations on frames, and ways of building them (though maybe I’m just not sure where to look). Either way, I hope my students find this a useful (if somewhat fleshed out) review of the localic material we’ve covered so far, and I hope that future readers find this an approachable introduction to the basics of locale theory.

Take care, everyone, and I’ll see you soon ^_^

PS: I’ve been reading a lot of locale theory lately, particularly while looking for references that showcase either explicit constructions or interesting use cases. I usually include references either in the text or in footnotes, but I’ll actually include a short bibliography here for the papers that I found particularly insightful:

Anel, Mathieu, and André Joyal. “Topo-Logie.” In New Spaces in Mathematics, edited by Mathieu Anel and Gabriel Catren, 1st ed., 155–257. Cambridge University Press, 2021. https://doi.org/10.1017/9781108854429.007.
Banaschewski, Bernhard, and Christopher J. Mulvey. “A Constructive Proof of the Stone-Weierstrass Theorem.” Journal of Pure and Applied Algebra 116, no. 1 (March 28, 1997): 25–40. https://doi.org/10.1016/S0022-4049(96)00160-0.
———. “A Globalisation of the Gelfand Duality Theorem.” Annals of Pure and Applied Logic 137, no. 1 (January 1, 2006): 62–103. https://doi.org/10.1016/j.apal.2005.05.018.
Blechschmidt, Ingo. “Generalized Spaces for Constructive Algebra.” ArXiv:2012.13850 [Math], December 26, 2020. http://arxiv.org/abs/2012.13850.
Borceux, Francis. Categories of Sheaves. Digitally printed version. Handbook of Categorical Algebra / Francis Borceux 3. Cambridge: Cambridge Univ. Press, 2008.
Chen, Xiangdong. “On Binary Coproducts of Frames,” n.d., 14.
Day, B. J. “Locale Geometry.” Pacific Journal of Mathematics 83, no. 2 (August 1, 1979): 333–39. https://doi.org/10.2140/pjm.1979.83.333.
He, Wei, and MaoKang Luo. “Completely Regular Proper Reflection of Locales over a given Locale.” Proceedings of the American Mathematical Society 141, no. 2 (June 5, 2012): 403–8. https://doi.org/10.1090/S0002-9939-2012-11329-2.
Isbell, John. “Product Spaces in Locales.” Proceedings of the American Mathematical Society 81, no. 1 (1981): 116–18. https://doi.org/10.2307/2044000.
———. “Atomless Parts of Spaces.” MATHEMATICA SCANDINAVICA 31 (June 1, 1972): 5. https://doi.org/10.7146/math.scand.a-11409.
Johnstone, Peter T. Stone Spaces. Paperback ed., Repr. Cambridge Studies in Advanced Mathematics 3. Cambridge: Cambridge Univ. Press, 1992.
Pelletier, Joan Wick. “Locales in Functional Analysis.” Journal of Pure and Applied Algebra 70, no. 1 (March 15, 1991): 133–45. https://doi.org/10.1016/0022-4049(91)90013-R.
Picado, Jorge, and Aleš Pultr. Frames and Locales: Topology without Points. Frontiers in Mathematics. Basel: Birkhäuser, 2012.
———. “Notes on the Product of Locales.” Mathematica Slovaca 65, no. 2 (April 1, 2015): 247–64. https://doi.org/10.1515/ms-2015-0020.
Vickers, Steven. “Geometric Logic in Computer Science.” In Theory and Formal Methods 1993, edited by Geoffrey Burn, Simon Gay, and Mark Ryan, 37–54. Workshops in Computing. London: Springer London, 1993. https://doi.org/10.1007/978-1-4471-3503-6_4.
———. “Compactness in Locales and in Formal Topology.” Annals of Pure and Applied Logic 137, no. 1–3 (January 2006): 413–38. https://doi.org/10.1016/j.apal.2005.05.028.
———. “Continuity and Geometric Logic.” Journal of Applied Logic, Logic Categories Semantics, 12, no. 1 (March 1, 2014): 14–27. https://doi.org/10.1016/j.jal.2013.07.004.

I feel like this is particularly economical for a few reasons:

First, posets and lattices are simple combinatorial objects that you can understand without much background in abstract algebra or topology. We also get two “levels” of categories out of this, since every poset is a category in its own right, but we can also consider the category of posets, or any one of the zoo of categories of lattices.

In fact, the zoo of lattice categories is nice, because it forces you to acknowledge that it’s the arrows that matter. After all, frames (which we’ll define soon) and complete heyting algebras are the same thing! We can only distinguish between the categories because the homomorphisms are different.

This means that we can see categorical constructions in multiple lights very quickly: Products in a poset are meets, while products in the category of posets are given by a poset of tuples. Adjoint functors between posets are galois connections, while adjoint functors between the categories of posets and meet semilattices might be a free/forgetful pair, etc. ↩
The definition given on the nlab is nice because it make the analogy with topoi incredibly clear. It’s an easy exercise that our definitions are equivalent. ↩
As a nice exercise:

Show that every frame is also a Heyting Algebra. You can do this with abstract nonsense (use the adjoint functor theorem) or directly (give an explicit expression for the arrow $a ⟹ b$ ).

You should do whichever comes less naturally to you (or both, if neither comes naturally).

As a part 2, you should show that defining frames to be complete heyting algebras is incorrect, since morphisms of heyting algebras should preserve $⟹$ , whereas frame homomorphisms might not.

(You can see this mathoverflow question if you need a hint) ↩
That I can think of right now ↩
There’s actually a lot to say about this construction! It turns out that $D P$ is the same thing as $[P^{op}, 2]$ , the monotone maps from $P^{op}$ to the two element poset ${0, 1}$ with $0 \leq 1$ .

Then $D P$ is nothing but the “presheaves on $P$ ” if we enrich over $2$ instead of $Set$ . This makes it clear that it should be the free way of adding joins (colimits) to $P$ , by analogy to the presheaves on a category $C$ being the “free cocompletion” of $C$ .

Again, there’s a lot to say here, since frames/locales are analogous in many was to grothendieck topoi, and this method of getting a locale by looking at “presheaf posets” is one instance of that analogy! ↩
Notice that we’re assuming the intersection of two basic opens is itself basic open. The usual definition is that the intersection of two basic opens merely contains a basic open – this seems like a property that should have a name, but I don’t know of one. Hopefully someone can leave a comment clarifying this ^_^

Either way, we’ll relax this assumption later on in the post! ↩
Which I’d like to prove in its own blog post… hopefully a shorter one, since the proof really isn’t that bad.

For the impatient reader (or if I never get to it) you can find a proof in Johnstone’s Stone Spaces, section II.1.7 ↩
This is yet another analogy to topos theory. See here for more ↩
Though it does make the construction go slightly more smoothly. This, again, is analogous to the setting of sites on a category in topos theory, where assuming your category has pullbacks makes the construction a bit simpler. ↩
Notice this quotient is taken in the category of suplattices, so it’s not obvious that we should actually get a frame out the other side.

This is where the flat stability axiom comes into play, since it tells us (roughly) that we can “pull back” a cover $A$ of $p$ to a cover $B$ of $q$ whenever $q \leq p$ . Since for any $p$ and $r$ we’ll have $p \land r \leq p$ , this will let us show the distributivity axiom for frames.

For a full proof, see theorem 5 in Vickers’ Compactness in Locales and in Formal Topology ↩
We have the usual structural rules, and all the connectives work in the traditional way, with the rules for infinite disjunction being the natural generalization of the usual disjunction rules. We won’t need to know the intricacies of the system here, so I’ll omit a full description, but the interested reader can find one in section D1.3 of the elephant. ↩
That is, the set of geometric formulas with the given primitive propositions ↩
So, for instance, given two equivalence classes of formulas $[φ]$ and $[ψ]$ , their meet in the frame will be given by the class of their conjunction $[φ \land ψ]$ .

Similarly, for (infinitary) joins and disjunction.

This is why we need to quotient by provable equivalence, because $φ \land (ψ \land θ)$ and $(φ \land ψ) \land θ$ are technically two different formulas. Though they’re provably equivalent, which is all we need to claim that $\land$ is associative! ↩
You’ll often hear logicians talk about formulas “up to $T$ -provable equivalence”.

This is what we’re talking about! ↩
See, for instance, Pelletier’s excellent survey Locales in Functional Analysis. ↩
Though this sounds much more exciting than it is… Prepare to be underwhelmed :P ↩
In the same way that propositional geometric theories all have a classifying locale, more general predicate geometric theories admit a classifying topos!

Since every algebraic theory is geometric, this tells us that there’s a topos $G$ so that for any topos $E$ , the “ $E$ -points of $G$ ” are exactly group objects in $E$ !

This also plays nicely with the intution that $E$ -points of $G$ are “points of $G$ varying continuously in $E$ ”, since a group object in a sheaf topos (say) is exactly a sheaf of groups. That is, a family of groups varying continuously in the base space of the topos! ↩
And this is one of the big reasons to favor locales over topological spaces! Locales behave much better under this interpretation, basically because their theorems are provable constructively. Since the slice category of locales over $Y$ is equivalent to the category of locales internal to $Sh (Y)$ , this means that anything we prove (constructively) about locales is immediately true for bundles of locales as well! ↩