Monoidal Monoidoidoids
21 Aug 2022 - Tags: featured
So I was on the nlab the other day, and I saw a fantastic joke: A 2-category is “just” a monoidal monoidoidoid! Here’s a screenshot in case the nlab page for 2-categories changes someday:

There’s a thing called the Category Theorist’s “Just”, which describes the joy that many category theorists take in telling other mathematicians that an X is “just” a [categorical gibberish]. This is often seen as unhelpful at best and annoying at worst by other mathematicians, and I think there’s room for a bit of honest discussion here, if you’ll give me a second to preach (I’ll get to the joke in the title soon, I promise).
I’ve met category theorists who do this purely to try and look smart, and to make other people who aren’t fluent in abstract nonsense feel inadequate.
I do not like these category theorists.
That said, when you spend a long time around the language of category theory, you really do build an intuition for what certain common constructions (monoids, adjunctions, co/limits, etc.) look like in certain common kinds of categories (algebraic categories, topological categories, functor categories, etc.).
In this way, if someone knows the lingo, you can really convey a lot of information very efficiently by the use of this language. For instance, I genuinely think the meme
monads are “just” monoids in the category of endofunctors
is a useful way to explain monads provided you’re talking to another category theorist. It’s not even that hard to imagine somebody who knows things about algebra internal to functor categories, but who doesn’t know things about monads!
Of course, this quip is entirely unhelpful if you’re trying to explain monads to a software engineer with little to no knowledge of category theory…
Now, I personally try to never use the category theorist’s “just” when I’m talking to someone who I don’t know well. Or if I do, I always make sure to preface it by a question of how much category theory they know, and the promise that I can translate whatever abstract nonsense I say into concrete terms if they want me to.
The unique exception is when making jokes, because sometimes it’s hilarious to give the worst possible definition for a simple object. And 9 times out of 10 that definition will be categorical in nature.
This leads to a fun little game where you try to obfuscate a definition as much as possible, and if you’re like me, it’s also fun to deobfuscate the definition to see why it works! Which (finally) leads us to the title of this post:
Why is a 2-category “just” a Monoidal Monoidoidoid?
This is possibly the worst way to introduce 2-categories, and has the added benefit of being incredibly silly to say out loud. 10/10. No notes. I’m absolutely adding this to my vocabulary.

But what does it mean?
Well first things first, we want to parenthesize this correctly. A 2-category is a (monoidal monoidoid)oid.
Category theorists love to put the suffix “oid” at the end of a preexisting word. In general if X is a gadget that can be seen as a one-object category, then an X-oid will be that same kind of gadget, but allowing multiple objects.
For instance, a group can be seen as a one object category where every arrow is invertible. So a groupoid is any category where every arrow is invertible.
Similarly, an algebra over a field
The exception is monoid, which historically already has an “oid” suffix. A monoid is “just” a one object category, so a monoidoid should be any category. Obviously nobody calls categories “monoidoids”, but it’s kind of cute to know we could.
Next we need to understand monoidal monoidoids. That is, monoidal categories. We’re about to oid-ify this into (monoidal monoidoid)oids, so we should be able to view a monoidal category as a kind of one-object category in its own right.
We know that monoidal categories are categories
Inspired by this, say
Of course,
So then, a monoidal category
So finally, we see that we can oid-ify the notion of monoidal category by
removing the assumption that there be a single object
Now a “monoidal category”-oid (or a monoidal monoidoid oid) has
- Objects
- 1-Arrows between the objects
- 2-Arrows between the 1-arrows
We can compose 1-arrows in the expected way, and we can compose 2-arrows vertically (which is the obvious way) and horizontally (which says that 2-arrows are compatible with composition of 1-arrows)3.
Of course, this is the usual definition of a (strict) 2-category! Now you’re officially in on the joke ^_^

Another short post for once! I’m once again on my way to New York tonight to see some friends, but when I saw “monoidal monoidoidoid” on the nlab I literally laughed out loud. I spent a bit of time yesterday figuring out what it meant (though in hindsight the nlab page just tells you…) and wanted to write this up and share it today before I head to the airport.
As another little life update, I was at BLAST last week, and had a ton of fun4! It was great to hang out with other logicians, and it’s super exciting to know that there’s likeminded people so near me – It was getting kind of lonely being the only logician at UC Riverside. Everyone was super nice, and I had a lot of great conversations. I’ll definitely be at BLAST next year, and I might try to spend a bit of time at Chapman too.
For now, though, I have to start packing. Take care everyone, and see you soon ^_^
-
Do you see why? As a hint, multiplication in your algebra becomes composition in the category, just like group multiplication becomes composition. ↩
-
Concretely, if we have 2-arrows
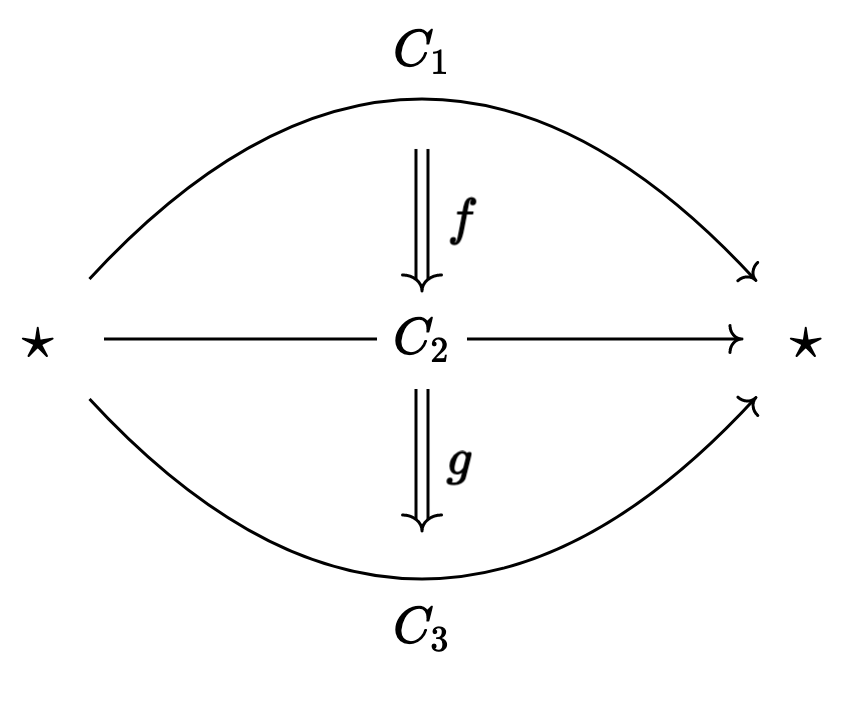
If instead we have objects
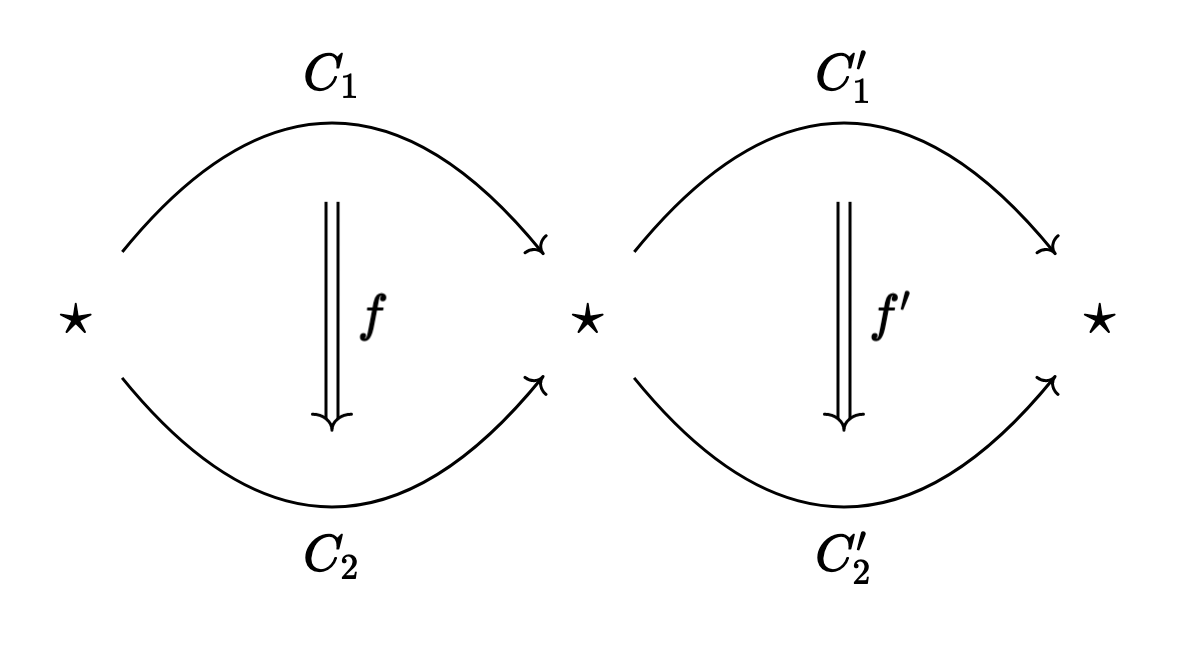
then (recalling that the “composition”
-
Another way to see this is to say that a monoidal category is a category with one object
Then we recover (strict) 2-categories as the oid-ified version of this. That is, as a category where each homset
This is perfectly analogous to the case of
-
One could say I…. Had a blast? :P ↩