A truly incredible fact about the number 37

08 Nov 2023 - Tags: sage , featured

So I was on math stackexchange the other day, and I saw a cute post looking for a book which lists, for many many integers, facts that Ramanujan could have told Hardy if he’d taken a cab other than 1729. A few days ago OP answered their own question, saying that the book in question was Those Fascinating Numbers by Jean-Marie De Koninck. I decided to take a glance through it to see what kinds of facts lie inside (and also to see just how many integers are covered!). Not only was I overwhelmed by the number of integers and the number of facts about them, the preface already includes one of the single wildest facts I’ve ever heard, and I have to talk about it here! Here’s a direct quote from the preface:

37, the median value for the second prime factor of an integer; thus the probability that the second prime factor of an integer chosen at random is smaller than 37 is approximately $\frac{1}{2}$ ;

My jaw was on the floor when I read this, haha. First it sounded totally unbelievable, since 37 is a tiny number in the grand scheme of things. Then it started to sound slightly more plausible… After all, about half of all integers have $2$ as their smallest prime factor. It makes sense that smaller primes should be more frequent among the smallest factors of numbers! But then I thought “how can you possibly prove this!?”. I’m not much of an analytic number theorist¹, but I know that they have good estimates on a lot of facts like this. I decided it would be fun to try and find and understand a proof of this fact, and also write some sage code to test it!

So then let’s go ahead and do it ^_^

First, I think, the sage code. I want to know if this really works!

“Obvoiusly” there’s no uniform distribution on the natural numbers, so what does it even mean to choose a “random” one? The way the number theorists usually solve this problem is by fixing a large number $N$ and looking at the probabilities when you pick a random number between $1$ and $N$ . Then you look at the $N \to \infty$ limit of these probabilities.

So for us, we’ll want to first fix a large number $N$ and then work with numbers $\leq N$ . For $N$ kind of small, we can just find the second prime factor of each number $\leq N$ and check the median!

xxxxxxxxxx
 
def getSecondSmallestFactors(N):
    data = []
    for n in range(1, N):
        fs = factor(n)
        if len(fs) > 1:
            second_smallest = fs[1][0]
            data += [second_smallest]
        else:
            # If there's only one prime factor
            # say the second prime factor is infinity
            data += [oo]
    
    return data
​
@interact
def _(N=input_box(10^5, width=10, label="$N$")):
    data = getSecondSmallestFactors(N)
​
    med = numpy.median(data)
    show("median second prime: ")
    show(med)
    show("")
​
    below37 = len([d for d in data if d <= 37]) / N
    show("fraction of numbers whose second prime is at most 37: ")
    show(below37.n())
    show("")

Help | Powered by SageMath

Messages

When I first ran this code, it honestly felt like magic, haha. What the hell is going on here!?

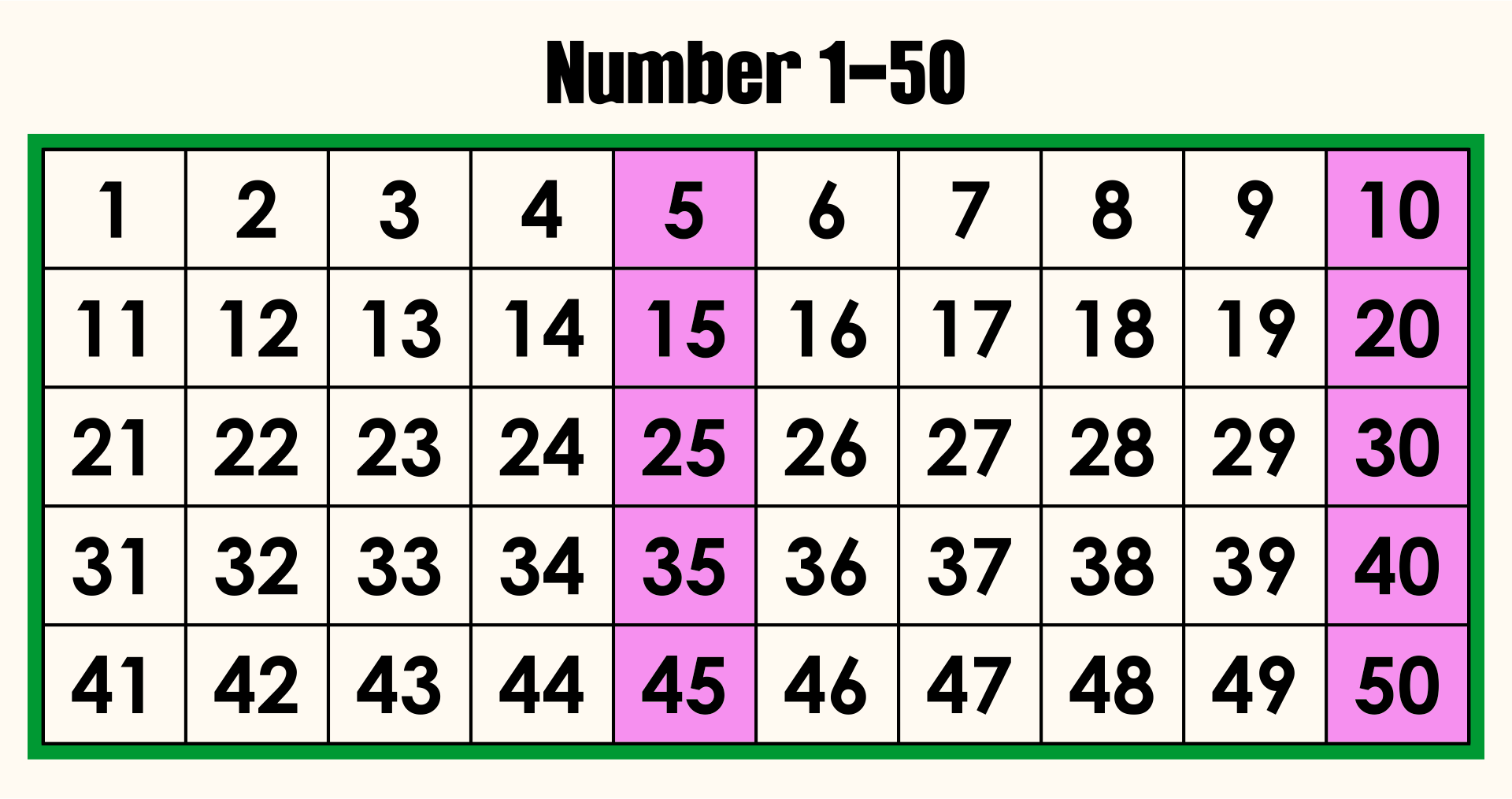
The key idea, found in a paper of De Koninck and Tenenbaum², is that we can compute the density of numbers whose second prime is $p$ (which the authors denote $λ_{2} (p)$ ) by cleverly using the ideas in the Sieve of Eratosthenes!

Let’s do a simple example to start. What fraction of numbers have $5$ as their second prime? In the language of the paper, what is $λ_{2} (5)$ ?

Well it’s not hard to see that the numbers whose second prime is $5$ are those numbers whose prime factorization looks like

2^{a} 3^{0} 5^{b} \dots

2^{0} 3^{a} 5^{b} \dots

so we need to count the density of numbers of these forms.

But a number is of the first form ( $2^{a} 3^{0} 5^{b} \dots$ ) if and only if it has a factor of $2$ , a factor of $5$ , and no factors of $3$ .

To bring this back to elementary school³, we can highlight all of our numbers with a factor of $2$

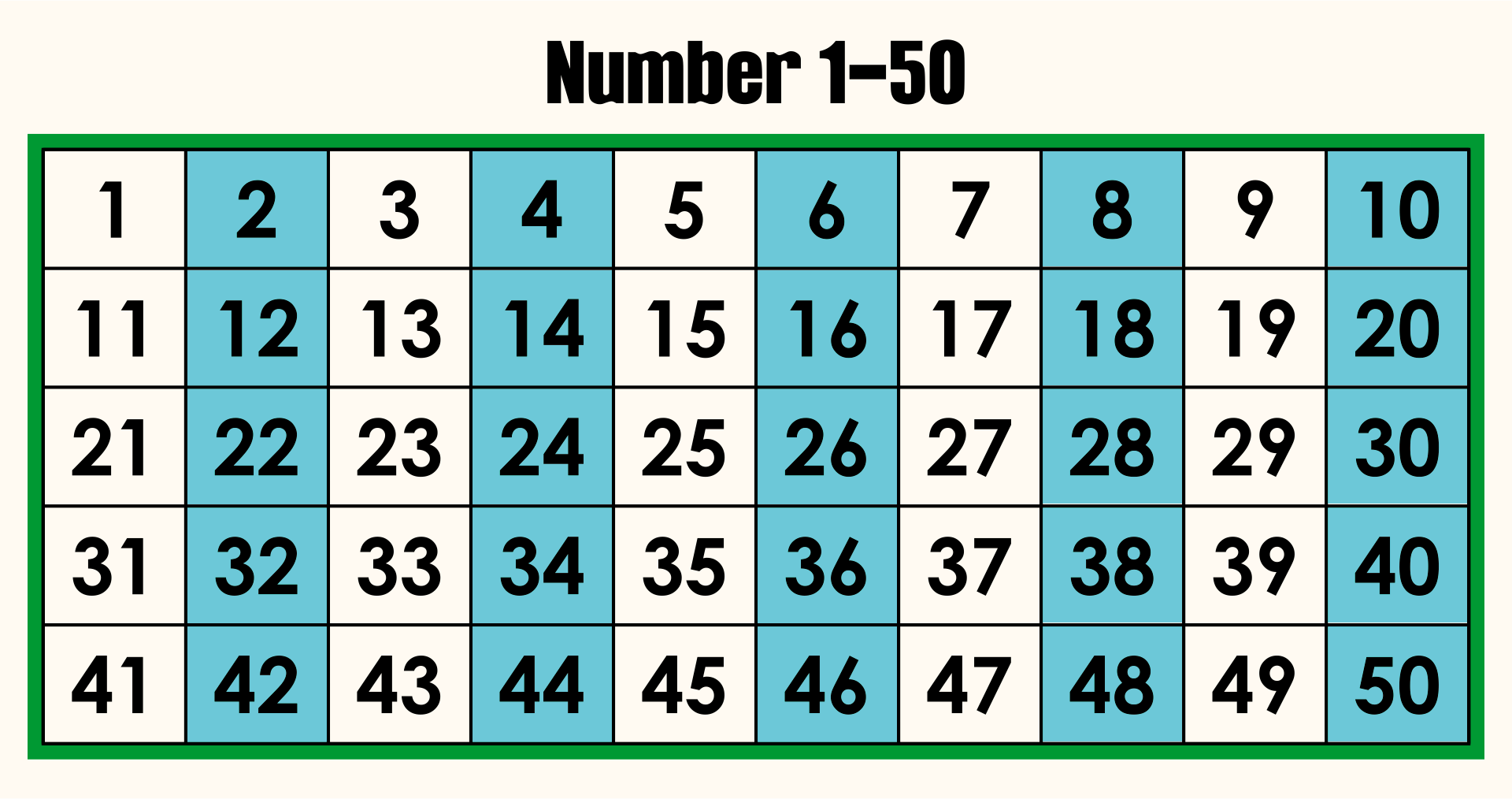
numbers with no factors of $3$

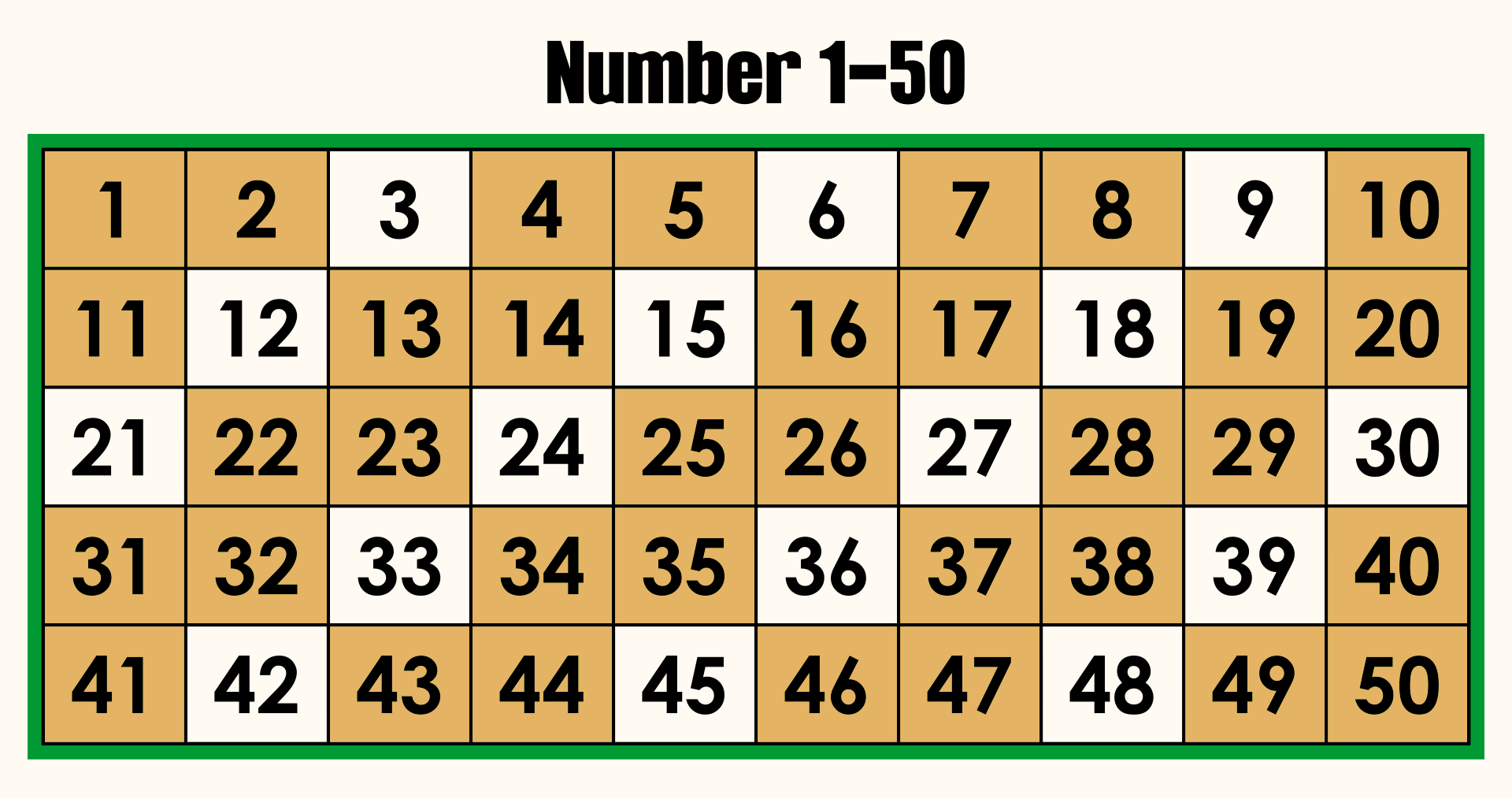
and numbers with a factor of $5$

Then the numbers whose prime factorization starts $2^{a} 3^{0} 5^{b} \dots$ are exactly the numbers highlighted by all three of these colors!

It’s intuitively clear that $\frac{1}{2}$ the numbers are blue, $\frac{2}{3}$ are orange, and $\frac{1}{5}$ are pink. So taken together, $\frac{1}{2} \cdot \frac{1}{5} \cdot \frac{2}{3} = \frac{1}{15}$ of numbers are of this form!

So now we have our hands on the density of numbers of the form $2^{a} 3^{0} 5^{b}$ , but this is only one of two ways that $5$ can be the second smallest prime. A similar computation shows that $(1 - \frac{1}{2}) \cdot \frac{1}{3} \cdot \frac{1}{5} = \frac{1}{30}$ of numbers are of the form $2^{0} 3^{a} 5^{b}$ .

It’s easy to see that these sets are disjoint, so their densities add, and $\frac{1}{15} + \frac{1}{30} = \frac{1}{10}$ numbers have $5$ as their second smallest factor!

Now with the warm-up out of the way, let’s see how we can compute $λ_{2} (p)$ for our favorite prime $p$ !

We’ll play exactly the same game. How can $p$ be the second smallest prime? Exactly if the prime factorization looks like

p^{b} q^{a} \prod_{q \neq r < p} r^{0}

for some $q < p$ .

But we can count these densities as before! For each choice of $q$ , we know that $\frac{1}{p}$ numbers are multiples of $p$ , $\frac{1}{q}$ are multiples of $q$ , and for each $r$ we know $(1 - \frac{1}{r})$ numbers are not multiples of $r$ ! For each $q$ , then, we want to land in the intersection of all of these sets, then we want to sum over our choices of $q$ . Taken together, we see that

The density of numbers whose second prime is $p$ is

λ_{2} (p) = \sum_{q < p} \frac{1}{p} \frac{1}{q} \prod_{q \neq r < p} (1 - \frac{1}{r})

We can rearrange this to

$λ_{2} (p) = \frac{1}{p} [\prod_{q < p} (1 - \frac{1}{q})] \sum_{q < p} \frac{1}{q} {(1 - \frac{1}{q})}^{- 1}$

As a cute exercise, write $λ_{k} (p)$ for the density of numbers whose $k$ th prime is $p$ .

De Koninck and Tenenbaum mention in passing that

λ_{k} (p) = \frac{1}{p} [\prod_{k < p} (1 - \frac{1}{q})] s_{k - 1} (p)

where $s_{j} (p) = \sum \frac{1}{m}$ is a sum over all $m$ who have exactly $j$ prime factors, all of which are $< p$ .

Can you prove that this formula is correct⁴?

But remember the goal of all this! We want to know the prime $p^{*}$ so that half of all numbers have their second prime $\leq p^{*}$ . That is, so that the sum of densities

λ_{2} (2) + λ_{2} (3) + λ_{2} (5) + \dots + λ_{2} (p^{*}) \approx \frac{1}{2} .

But we can implement $λ_{2} (-)$ and just check for which prime this happens!

xxxxxxxxxx
 
def lambda2(p):
    """
    Compute the density of the set of n whose 2nd prime is p.
    See equation (1.3) in Koninck and Tenenbaum, 2002
    """
​
    s = 0
    out = 1
​
    for q in Primes():
        if q >= p:
            break
        out *= (1 - (1/q))
​
    for q in Primes():
        if q >= p:
            break
        s += (1/q) * (1 - (1/q))^(-1)
​
    out *= s
    out *= 1/p 
​
    return out
​
total = 0
for p in Primes():
    if total > 0.5: break
​
    l = lambda2(p)
    total += l
​
    show("{} of numbers have {} as their second prime".format(l.n(),p))
    show("so {} of numbers have second prime at most {}".format(total.n(), p))
    show("")

Help | Powered by SageMath

Messages

Again we see that $37$ is the prime where roughly half of all numbers have something $\leq 37$ as their first prime! So we’ve proven that $37$ is the median second prime!

Also, this shows that we expect the actual density to be $\approx .5002$ . If we set $N = 10^{7}$ in the code from the first half⁵ to get a better approximation, we get $.5002501$ , which is remarkably close to the truth!

As another cute exercise – using the ideas in this post, can you compute the median third prime?

As a (much) harder exercise⁶, can you get asymptotics for how the median $k$ th prime grows as a function of $k$ ?

Thanks for hanging out, all! This was a really fun post to write up, and I’m really excited to share it with everybody! This fact about $37$ was all I could think about for like a week, haha.

I have more blog posts coming, of course, so I’ll see you all soon!

Stay safe, and stay warm ^_^

Absolutely the understatement of the year ↩
Sur la loi de répartition du k-ième facteur premier d’un entier

Yes, this paper is in french, but it’s really not so hard to read, especially with liberal use of google translate. Though if you want to avoid reading it, I’ve done the hard work for you, and everything in this blog post is in english.

It also wasn’t too hard to find this paper, thankfully. It’s mentioned in a footnote in the entry for $37$ in Those Fascinating Numbers, so I had a decent starting point. ↩
I literaly got the base image by googling “grid of numbers high res” and clicking the first result, which was for elementary schoolers ↩
It might be helpful to remember a generating function trick that shows up fairly often (for instance in partitions and the riemann zeta function):
$\sum \frac{1}{n} = \prod_{p} {(1 - \frac{1}{p})}^{- 1}$
Don’t worry that this sum diverges for now. Just take note of why these two sides are equal. You should expand each term of the right hand side as a geometric series, then check what happens when you foil. ↩
(and run it locally, since factoring numbers that big takes so long that the online sagecell times out) ↩
If you read french, the De Koninck and Tenenbaum paper we’ve been referencing all post (Sur la loi de répartition du k-ième facteur premier d’un entier) is actually all about analyzing these asymptotics!

If we write $p_{k}^{*}$ for the median $k$ th prime, then they show:
$\log \log p_{k}^{*} = k - b + O (\frac{1}{\sqrt{k}})$
where $b = \frac{1}{3} + γ - \sum_{p} (\log ((1 - 1 / p)^{- 1}) - 1 / p)$ and $γ$ is the Euler-Mascheroni Constant. ↩