Proving Another "Real Theorem" with Topos Theory
25 Mar 2024 - Tags: topos-theory
Another day, another post that starts with “So I was on mse…”, lol.
Somebody asked whether maximizing over a compact set is a continuous thing
to do. That is, given a continuous function
If you’re me, this looks an awful lot like the usual
extreme value theorem, but where
“everything in sight depends continuously on a parameter from
Depending on your experience with bundles, you might be aware that
the usual way to encode a “family of sets
I bet you weren’t expecting a cute exercise this early in the post!
Can you show that a family of functions
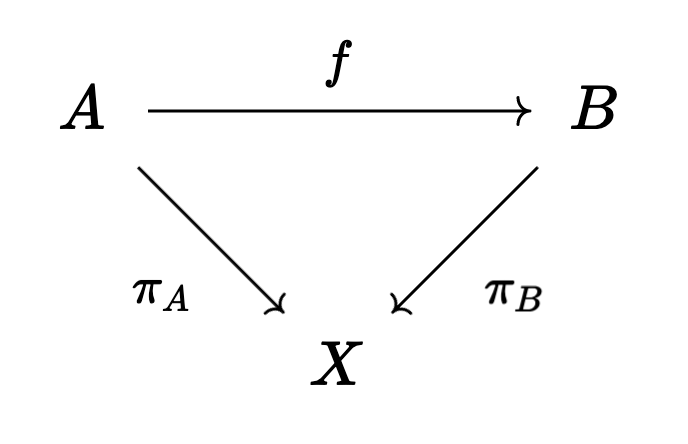
Recall we’re thinking of the sets
To go from the family
So the constant family
If you’ve been exposed to some ideas in topos theory, you should be screaming
something to do with the “internal logic” right now! Indeed, a theorem inside
the topos of sheaves on
So then, we want to get our hands on a constructive proof of the extreme value theorem. Typically constructive theorems which assert the existence of something (in this case, a maximum) require some ~bonus assumptions~ which are invisible in the classical case. This is because existence is a much stronger phenomenon constructively4.
To start, we probably want to be working with locales instead of
topological spaces. Since the person on mse was happy with "extreme value theorem"+"locale" to see if someone has
already done what we’re looking for, and our optimism is quickly rewarded!
We find Graham Manuell’s slides from TACL 2022 which give a
constructive proof of the following:
If
Let’s say a few words about what all these weird adjectives mean!
First, let’s handle the easiest one: Compact.
The most familiar definition of compactness is that every open cover
has a finite subcover. Precisely, if
However, constructively it’s better to avoid saying the word “finite” if you can. The notion of finiteness splits into different inequivalent notions (kuratowski-finite, bishop-finite, dedekind-finite, etc) which makes the whole thing a bit of a mess5. For this reason, there’s a different, equivalent definition of compactness which we often prefer:
We say
As a cute exercise, prove these two definitions are equivalent! Try your hardest to make sure your proof is constructive!
There’s one last angle on compactness that I want to emphasize here as well:
We say a locale is compact if universal quantification is open. That is,
if
The next adjective on the list is Overt. This is
a kind of tricky notion to understand at first, since it’s invisible classically.
We say a locale
There’s an equivalent characterization of overtness, which is often useful
in practice. We want to check that the unique map
However, recall that in a sheaf topos
Lastly, we say that a locale is Positive iff every
open cover must be inhabited. That is, if
Recall we say
Now, let’s outline the proof from Manuell’s slides10. Recall a
Dedekind Real is a pair of cuts
- if
- if
- if
- if
- If
- If
- If
If you haven’t seen this before, we think of
Now, finally, for the proof idea:
Then, we’ll use positive compactness to build
Lastly, we need to show
that the
Note how (after externalizing) this is really the same argument that Sangchul Lee gave in the accepted answer on mse!
First we show that
Then we show that
The compatibility conditions basically amount to checking your upper and lower semicontinuous functions are the same, but since Sangchul’s answer is working with a single function the whole time there’s no need to verify that.
So now we have this constructive theorem. What does it actually tell us after we externalize?
Well, you can chase through the definitions of compact, overt, and positive
inside (say) a sheaf topos
First, as we alluded to in the introduction to this post,
a locale
From here, it’s not (too) hard to see that
So altogether we learn that
If
is continuous.
In particular, we answer the OP’s question! Taking
is continuous. As desired!
Ok! Thanks for reading, all! This felt like it took forever for what a short post it was, but I had a great time writing it. I’m flying home from the AMS Sectional today, where I gave a talk at the special session on Homotopy Theory and Category Theory in Interaction. I had a great time, and met a lot of really awesome people. It was a small group, which means we had lots of time to hang out and get to know each other.
I’ll write up some stuff about the conference (and my talk) soon, but for now I need to get ready to go to the airport! Stay safe ^_^.
-
I really don’t like Goldblatt’s Topoi as a book, but his section on the relationship between bundles over
-
Note that it’s possible to have constant fibres, without being the trivial bundle! In this case, even though each fibre is the same as every other, we glue them together in an interesting way! To be the trivial bundle, you need to know the fibres are all the same, and that we glued them together in the most naive way possible. For instance, the trivial
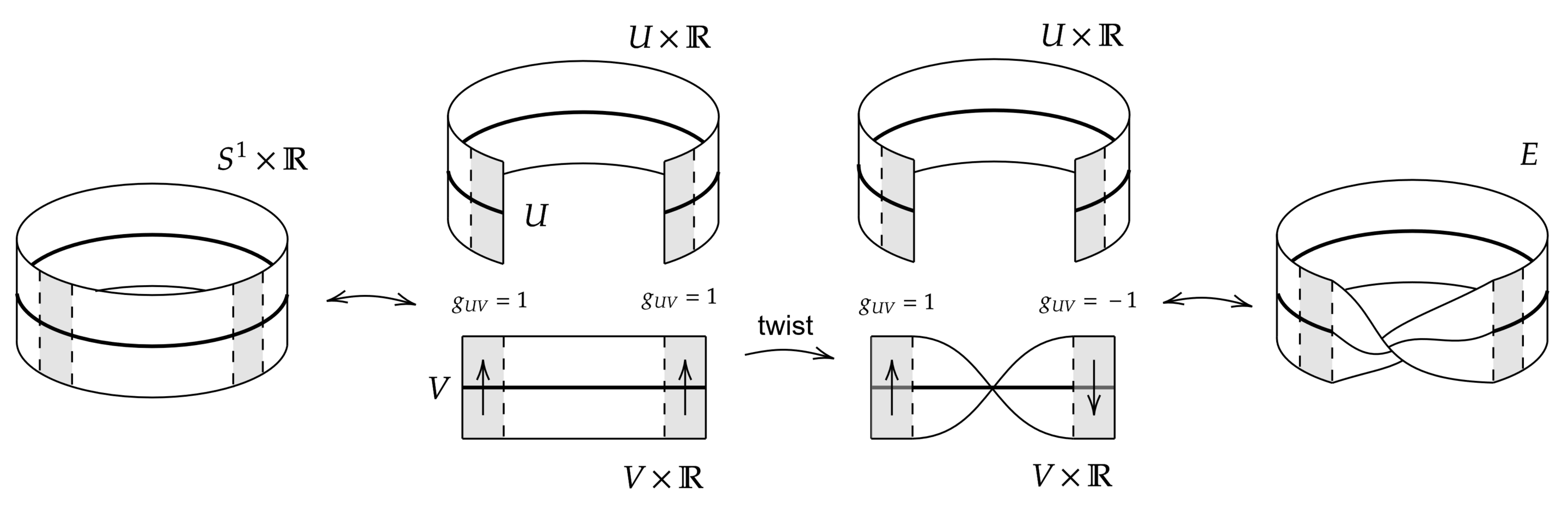
As a cute exercise, can you come up with two bundles over
-
Any type theorists in the room are probably screaming Dependent Sum right around now! That’s extremely fair, and I almost put something in the main post about this, but I ended up editing it out. ↩
-
As witnessed (pun intended) by the fact that, interpreted in suitable topoi, a constructive existence proof gives rise to free theorems saying there’s an algorithm that produces the desired object, or that the desired object can be defined continuously in a parameter, etc. This is exactly the phenomenon we’re trying to exploit, and we have to do work somewhere! ↩
-
I still haven’t taken the time to really familiarize myself with the various notions of finiteness, and how they “feel”. One day soon I want to, though. ↩
-
Recall a partial order
their joinEdit: There’s a mutual uppoer boundThis is really hiding kuratowski-finiteness again, since directedness guarantees that for any kuratowski-finite subset
-
I was curious about this, and Pedro pointed out that one direction is basically the classical tube lemma. I don’t actually see how to do the other direction (at least quickly) and I don’t really have time to think about it right now. If someone figures it out I’d love to hear about it in the comments! ↩
-
Constructively it’s still true that every locale with enough points is automatically overt (see the nlab). It’s a very mild condition, see the discussion here, for instance, or Paul Taylor’s Overt Subspaces of
-
Edit: July 7, 2024:
Graham and I talked about this on the CT Zuip back in March, since it’s not 100% obvious how this works.
In Graham’s notes, theorem 3.15 is a constructive proof that
So this tells us that,
We would love to use the “well known” equivalence between the category of internal locales in
That said, this particular situation is simple enough that we don’t need to worry about such things! In his notes, Graham actually proves that
There’s almost certainly a cleaner approach using Caramello and Zanfra’s recent machinery about relative topoi via stacks (see here), but I haven’t had time to learn any of these results. ↩
-
He, in turn, mentions was based on the treatment in Paul Taylor’s A Lambda-Calculus for Real Analysis. I actually have this paper saved, but it’s long and I wasn’t sure how easy it would be to translate Taylor’s results into language I’m more familiar with. Now that I’ve seen Manuell do it, though, I have plans to read this paper pretty soon! ↩
-
I’ve always gotten slightly annoyed, or at least laughed quietly to myself, when authors ask the reader to “recall” some fact that they quite possibly don’t know.
I really want this post to be done, though (I’ve been working on it for almost a month) and if I have to explain why upper/lower reals correspond to upper/lower semicontinuous functions I’ll never finish… I know, I tried.
You can find an extremely detailed treatment in Mac Lane and Moerdijk’s Sheaves in Geometry and Logic Chapter VI.8. Understanding this well is probably enough to work out that upper/lower reals correspond to upper/lower semicontinuous functions yourself (which will make a great exercise!). Depending on your experience, you might be helped by my old post on externalizing formulas inside a topos.
There’s also a great treatment in Johnstone’s Sketches of an Elephant, Chapter D4.7. This works out the case of lower reals and lower semicontinuous functions explicitly, but does so quite quickly. ↩
-
In fact we can say exactly which map it is! We want a locale map from
But given an open set
The desired map from
-
I feel kind of bad not proving these facts, since they’re not so hard? But I really am trying to finish this post quickly.
You can find a lot of this in Johnstone’s Elephant. In particular,
- Getting a locale map
- Compactness of
- Overtness of
- We’ve already talked about why positivity means
- Getting a locale map