Talk -- What is Factorization Homology?
27 Mar 2024 - Tags: my-talks
I was recently invited to speak at the AMS Sectional in Tallahassee, Florida. In particular, at the special session on Homotopy Theory and Category Theory in Interaction. The conference was this weekend, and I’m typing this up on my plane ride home. I had a great time, and met a lot of great people! The special session was pretty small, so we all got to talk to each other, and I got surprisingly close with the people I went out for lunch (and later, drinks) with!
I was nervous at first, since Florida… isn’t politically friendly towards trans people. Thankfully everybody that I interacted with was lovely, and I didn’t have any issues at all. What’s more, the campus was beautiful, and the surrounding area was surprisingly walkable. We had a 4 hour lunch break on the first day (which is part of how I got so close with my lunch group), and after we ate some great barbecue we all hung out under some fantastic trees.
I also felt safer because I was hanging out with Kaya Arro, a postdoc at UCR, for basically the whole time. They were great company, and also helped a ton with silly homotopy questions while I was making my slides (on the day before the talk…).
Anyways here are some of the trees right outside the conference building1!

It was like $400 cheaper to fly out on Monday evening, even though the conference ended on Sunday, so Kaya and I had almost a whole day to ourselves. We went to the FSU Museum of Fine Arts and walked around until it was airport time.
It was the perfect size museum for the amount of time we had, with some amazing installation pieces, and a whole section dedicated to book making! That was particularly exciting for me, since one of my best friends, Ashley Chan, is a super talented book maker!
These first few paragraphs were a bit bloggier than usual, but I had a great time and wanted to talk about it! Now that we’ve had a chance to catch up, though, let’s get to the math ^_^.
My talk was on Factorization Homology, and I split it up into three sections:
- Why?
- What?
- How?
In the first section, I wanted to provide some motivation for the technology, and to explain why it deserves to be called “homology”.
The second section was all about what factorization homology is, at least in broad strokes. I left out a bunch of details about orientation and framings since the talk was only 20 minutes and I wanted to stay light on my feet. This was also the section I got to express myself the most, since I view factorization homology through the lens of categorical logic2, and I was able to spend some time on that perspective.
The third section was on actually doing things with factorization homology. That is, on how we can really compute it, and how we can interpret what these computations mean. I wasn’t able to spend too much time on the interpretation, but I said a few words, and it was worth it for the extra time spent on a (sketchy version of a) simple example computation.
There were some great questions after the talk, including one from Philip Hackney (one of the organizers, and the person who invited me) which gave me the chance to talk about what factorization homology has to do with my research.
All in all, I think the talk went super well. I don’t think I came off as particularly manic, which can happen when I give short talks, and it seems like people were able to take some intuition away, which is everything I wanted! It helps that everyone at the conference was super nice, so I didn’t have to worry at all about being judged or grilled. I think people were in a particularly good mood, since I was the first talk after lunch, so everyone was full and happy, haha.
So then, in more detail, what all did we talk about?
In what follows, I’ll always mean
First, the why.
We recall that “classical” cohomology
This encourages a rather broad perspective, which says
that we can think of
If we’re calling this thing cohomology, it’s natural to ask which “classical” theorems in cohomology are true in this setting. And one natural theorem to want is Poincaré Duality.
One motivation for factorization homology is that it’s the right homology theory to make this “Nonabelian Poincaré Duality” true!
In the talk I said some words about this, but online there’s no need for me to say anything. If you’re interested, you should just go read Lurie’s notes on the topic instead. After all, I basically just paraphrased them in the talk!
If you insist on sticking around here, though, the idea is this:
To prove the “classical” poincaré duality
- The functors
- Just check that
- Conclude that, since every manifold
- Taking homology of both sides to get the claim.
Basically, a cosheaf is something we can compute for a big thing
by gluing together the computations for small things
(you should have something like Mayer-Veitoris in mind).
In particular, since every manifold is glued from copies of
Now, if we wanted to cook up a homology theory making some kind of “nonabelian poincaré duality” true, we might try something like this:
- Show
- Define the “nonabelian homology” of
- Use the cosheaf-ness to extend this definition to all manifolds by “doing what you have to do”.
This turns out to not quite work, but if we define “nonabelian homology” for all disjoint unions
we’re able to get the job done5!
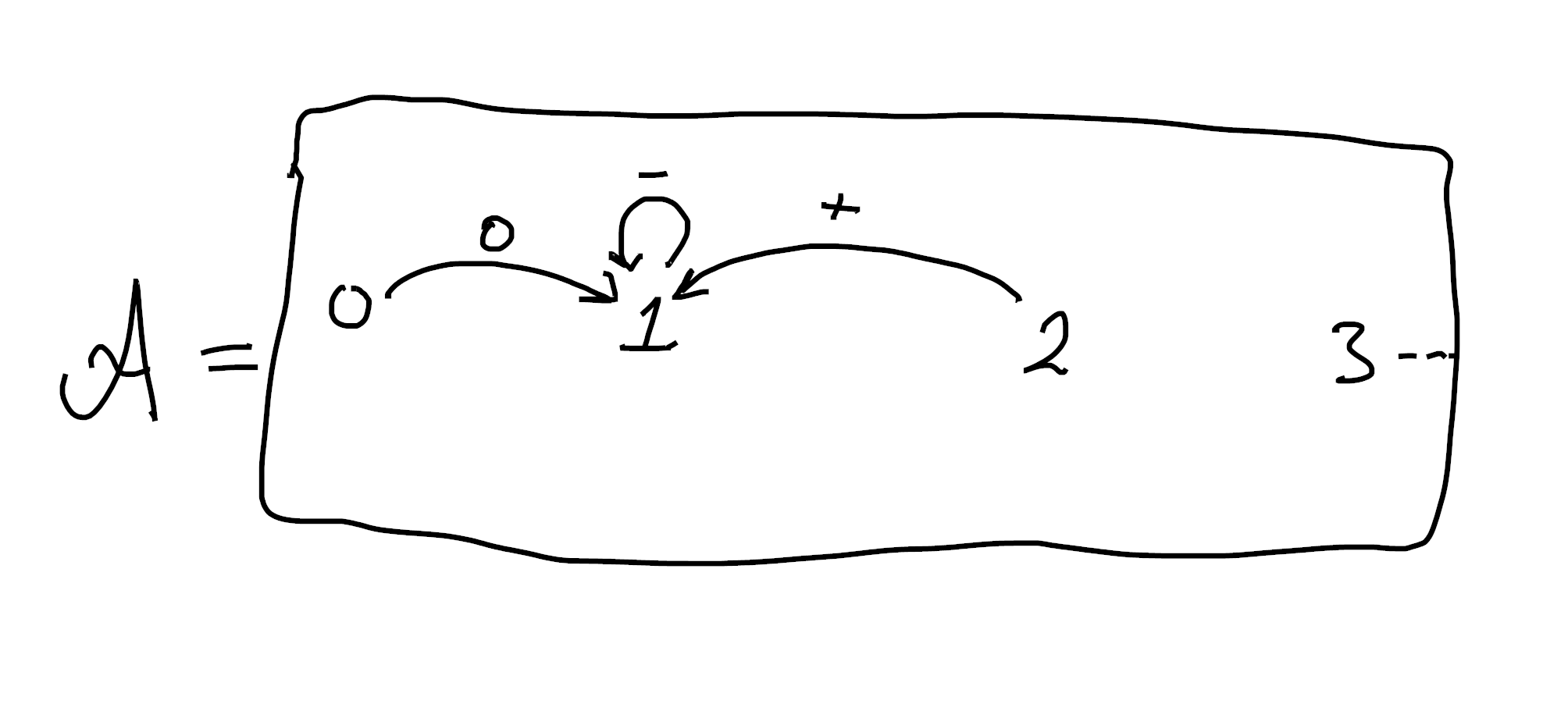
So then, we’ve found ourselves with a functor defined on
If you’re me, this feels a whole lot like a familiar story from categorical logic!
This, of course, is all part of the what!
At this point in the talk I took a quick diversion to remind people about Functorial Semantics. This was extra easy since in the morning session Valentina Zapata Castro spent some time talking about the lawvere theory for monoids!
In (1-categorical) functorial semantics, we have classifying categories
associated to algebraic theories. Then a model of that
theory is “just” a functor from the classifying category to
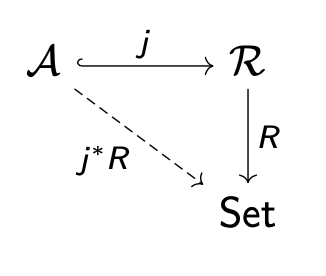
and the classifying category for rings

Indeed, a finite product functor
Note that we have an embedding
Now any ring
More excitingly, can we go the other way? Given a functor
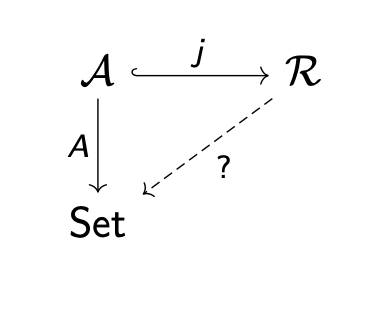
The answer, of course, is yes and it’s given by
left kan extension! This recovers the usual free ring on an
abelian group
Primed with this context, let’s look at our definition of factorization homology again:
We have a (symmetric monoidal) functor
So we have something that looks like some kind of algebra, which is
given by a functor out of
Doesn’t this setup sound familiar?
If
For instance, if
In particular, for a Collared Manifold
(that is, a manifold of the form

Similarly, if
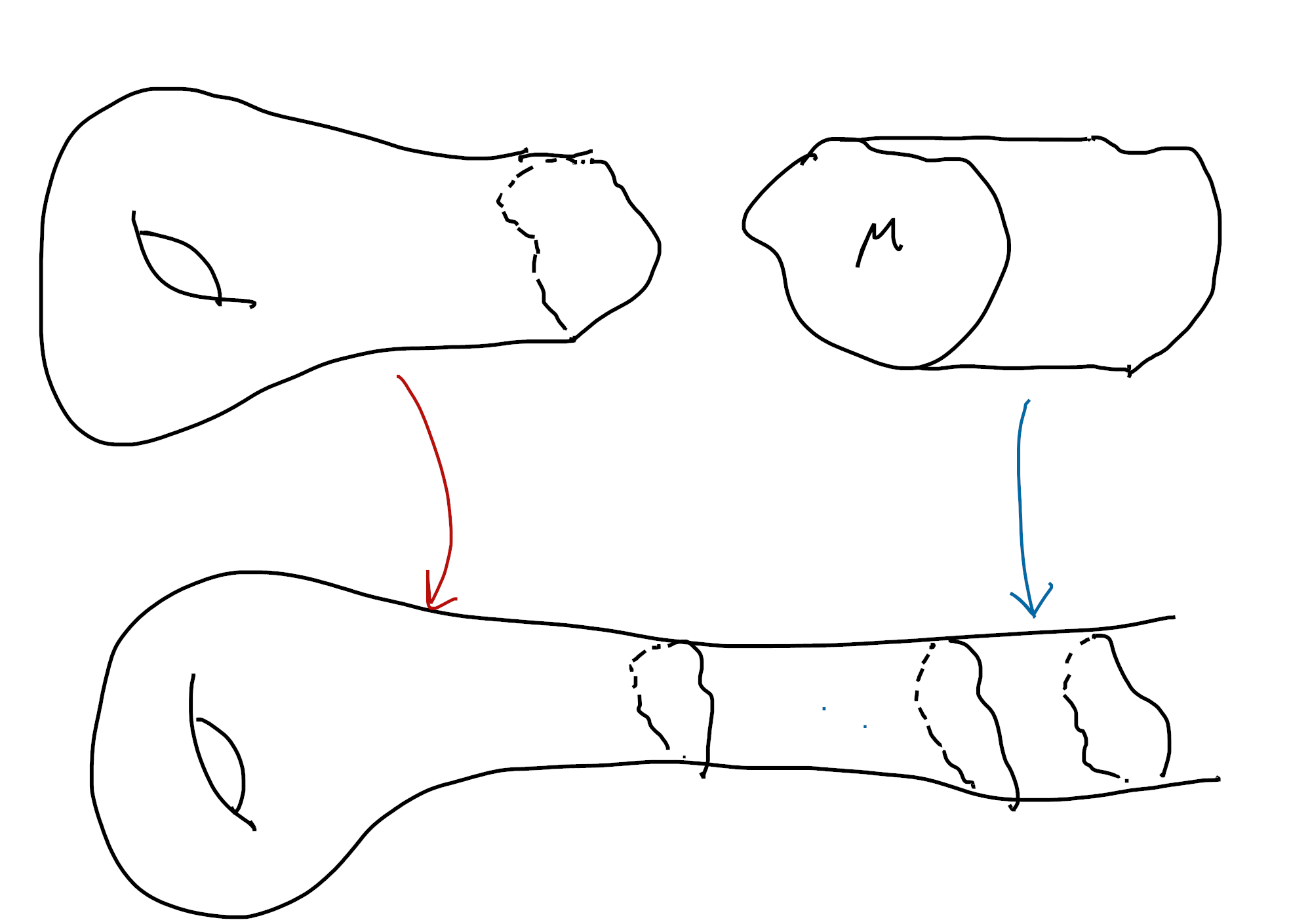
This brings us to the most important part of the How:
We can actually compute factorization homology by using “collared excision”:

If you want to read more about all of this, I highly recommend the relevant section in Juliet Cooke’s Thesis. If you want to really understand it well, there’s also Alaya and Francis’s Factorization Homology Primer and Hiro Lee Tanaka’s excellent lectures on the subject, which are available on youtube.
Thanks again for reading, all! I’m really pleased with how this talk went, and I’m happy to have made as many friends as I did at the conference.
It was great to be invited to speak in person somewhere for the first time, and to feel super welcomed in the homotopy theory world (which I’m only tangentially a part of… at least for now).
Stay safe, all, and we’ll talk soon!
What is Factorization Homology?
Ayala, Francis, and Rozenblyum introduced Factorization Homology in order to compare category theory and (topological quantum) field theory. It has since grown into a useful invariant of surfaces and algebras which, through excision, is often computable in practice. In this survey talk we will discuss the basics of factorization homology, emphasizing its connections to both homotopy theory and category theory (via infinity categories). Given time, we will also discuss some applications to the speaker’s ongoing dissertation work in skein theory.
The talk wasn’t recorded, but you can find the slides here.

-
The hilariously named “HCB” (Huge Classroom Building). ↩
-
Though honestly, I view most things through the lens of either categories or logic. So this should come as no surprise, haha. ↩
-
If you haven’t seen this before, it’s a super useful perspective to have on hand! For example,
Now (homotopy classes of) maps
But homotopy classes of maps
So, since these spaces are the same, we learn that complex line bundles on
-
This is one killer example of why people care about this kind of abstract nonsense. Not only do we need to know stuff about (co)sheaves, we also have to care about
This is basically because
-
This is basically because checking the cosheaf condition requires some version of Mayer-Veitoris. But the “usual” version of Mayer-Veitoris crucially uses the ability to add functions (since
But by working with disjoint unions of
You can read more about precisely what’s going on in Lurie’s notes. ↩
-
Precisely, the classifying category for the models of any algebraic theory is always the opposite of the category of the finitely generated free models.
So, for instance,
and
There’s a similar version of this story that works for essentially algebraic theories where we use the finitely presented models instead.
We’ve talked a bit about this on the blog before, and I have plans to talk quite a bit about it sometime in the future. ↩
-
I’m not going to tell you what that means, but here’s an illustrative example:
An
An
An
All
But you can imagine that, for