$\mathsf{B}\text{Diff}(\mathrm{\Sigma })$ Classifies $\mathrm{\Sigma }$-bundles

21 Dec 2024

I’ve been trying to learn all about topological (quantum) field theories, the cobordism hypothesis, and how to use $(\mathrm{\infty },n)$-categories. This is all in service of some stuff I’m doing with skein algebras (which are part of a “$3+1$ TQFT” often named after Crane–Yetter, but I believe the state of the art is due to Costantino–Geer–Haïoun–Patureau-Mirand), but it’s incredibly interesting in its own right and it’s been super fun to get a chance to learn more physics and learn way more about topology and higher categories.

Along the way, I was watching a lecture by Jacob Lurie where he mentions something that should probably be obvious (but wasn’t to me):

That is, given a manifold $M$ we have a natural bijection

$$\begin{array}{c}\{\text{homotopy classes of maps }M\to \mathsf{B}\text{Diff}(F)\}\\ ⟷\\ \{\text{fibre bundles }\pi :E\to M\text{ where every fibre is diffeomorphic to }F\}\end{array}$$

I asked about this in the category theory zulip, and got some great responses that still took me a while to digest. Actually, it wasn’t until I started reviewing a bunch of material on principal bundles¹ that everything clicked into place for me.

Over the course of this post, I’ll hopefully make this bijection obvious, and I’ll explain some facts about bundles along the way. This should serve as a nice quick blog post to write during my winter break since I’ve been extremely stressed for the last two months trying to get all my postdoc applications done². Thankfully it’s all finally behind me, and I’m back in New York with people I love, so I’m resting up and doing math again (which have both been fantastic for my mental health).

Let’s get to it!

---

First, let’s remember what a bundle even is. Say we have a base space $M$ and a map $\pi :E\to M$. Then for each point $m\in M$ we have the fibre $E_m={\pi }^{-1}(m)$, and so we can view $\pi$ as a family of spaces $(E_m)$ indexed by points of $M$. We think of $E_m$ as being “vertical” over $m\in M$, and we think of the topology on $E$ as telling us how these fibres are glued to each other “horizontally”³:

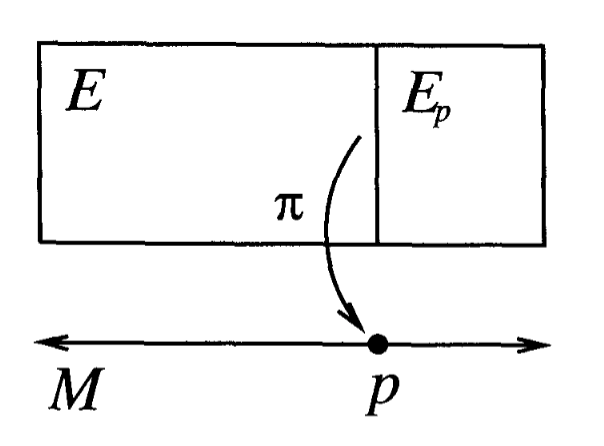
We say that $\pi :E\to M$ is a fibre bundle if it’s “locally trivial” in the sense that (locally) the fibres are all $F$, and these copies of $F$ are all glued to each other in the most obvious possible way. Because we mathematicians feel the need to make newcomers feel inadequate, we call this most obvious way the “trivial” bundle: $\pi :M\times F\to M$.

For a bundle to be locally trivial we don’t ask for it to literally be $M\times F$, that’s asking too much. Instead we ask that for every point $m\in M$ there should be a neighborhood $U_m$ so that ${\pi }^{-1}(U_m)\cong F\times U_m$⁴.

We say that such a bundle is a Fibre Bundle with Fibre $F$, and here’s a completely natural question:

Let’s think about how we might do this from a conceptual point of view, and that will lead us to the answer in the title of this post. Then we’ll reinterpret that conceptual understanding in much more concrete language, and hopefully explain why people care so much about principal bundles at the same time!

If we put our type theory hats on⁵, then we want to think about a fibre bundle as being a map from our base space $M$ into a “space of all $F$s”. Then we think of this map as assigning an $F$ to every point of $M$, and this is exactly⁶ the data of a fibre bundle!

But what should a “space of all $F$s” look like⁷? Well, as a first try let’s just take a huge manifold $\mathcal{U}$ and look at all copies of $F$ sitting inside it! For instance, we might take ${\mathbb{R}}^{\mathrm{\infty }}$, and then an “$F$ sitting inside it” is an embedding $\iota :F\hookrightarrow {\mathbb{R}}^{\mathrm{\infty }}$… almost! A choice of embedding has the ~bonus data~ of a parameterization, which an abstract “copy of $F$” wouldn’t have. We’re only interested in what’s morally the image of a particular embedding, so we should quotient out by reparameterization. Concretely, if $\phi :F\stackrel{\sim }{\to }F$ is a diffeomorphism, then $\iota$ and $\iota \circ \phi$ represent the same “copy” of $F$ in ${\mathbb{R}}^{\mathrm{\infty }}$, so we find ourselves interested in the space

$$\{\iota :F\hookrightarrow {\mathbb{R}}^{\mathrm{\infty }}\}/\text{Diff}(F).$$

Now it feels like we made a choice here, taking $\mathcal{U}={\mathbb{R}}^{\mathrm{\infty }}$, but we can worm our way out of this choice with homotopy theory! Indeed it’s believable that $\{\iota :F\hookrightarrow {\mathbb{R}}^{\mathrm{\infty }}\}$ should be contractible, since if $F$ is finite dimensional then any two embeddings lie in a small subspace of ${\mathbb{R}}^{\mathrm{\infty }}$, so there’s plenty of room to homotope them into each other. Then for any two such homotopies there’s still room to fill in the resulting circle, and so on. Since the space of embeddings is contractible, up to homotopy we’re working with⁸

$$\star /\text{Diff}(F)$$

and if we make “$\mathcal{U}$ is sufficiently large” mean “the space of embeddings of $F$ in $\mathcal{U}$ is contractible”, then we’ll get $\star /\text{Diff}(F)$ independent of this choice. Of course, $\star /\text{Diff}(F)$ is frequently called the Classifying Space $\mathsf{B}\text{Diff}(F)$, and so we’re halfway to our goal!

We normally think of $\mathsf{B}G$ for a group $G$ as an object classifying “principal $G$-bundles”, so that a map $M\to \mathsf{B}G$ is the same thing as a bundle over $M$ whose fibres are all isomorphic to $G$… So, naively, it sounds like a map $M\to \mathsf{B}\text{Diff}(F)$ should be the data of a bundle over $M$ whose fibres are $\text{Diff}(F)$! But we wanted a bundle over $M$ whose fibres are $F$! What gives?

The answer comes from the Associated Bundle Construction, which is the reason to care about principal bundles at all! In a remarkably strong sense, we can understand every “$G$-bundle” as long as we’re able to understand the principal $G$-bundles! Let’s see how, then use it to solve our problem in a (more) down-to-earth way.

---

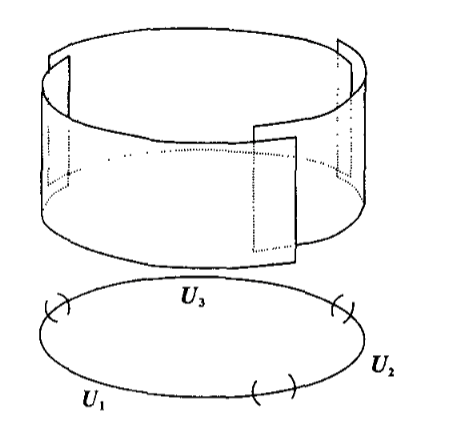
Concretely, we might understand a fibre bundle by picking a good open cover $\{U_{\alpha }\}$. Then we pick local trivializations ${\phi }_{\alpha }:{\pi }^{-1}(U_{\alpha })\stackrel{\sim }{\to }{U}_{\alpha }\times F$.

If we want to answer a (local) question about the bundle, we can use one of these ${\phi }_{\alpha }$s to transfer the question to a question about $U_{\alpha }\times F$, which is often easier to work with. But crucially we need to know that we’ll get the same answer no matter which of these “charts” $U_{\alpha }$ we work with. For instance, say our fibres are all $\mathbb{R}$. Then a natural question might be “is this element of the fibre $0$?”. If we always glue $0$ to $0$ then we get a consistent answer, but if at some point we glue $0$ in $U_{\alpha }$ to $1$ in $U_{\beta }$ then the answer will depend on which chart we use to do the computation!

It turns out that more fundamental than the particular choice of trivialization are the “transition maps” ${\phi }_{\beta }\circ {\phi }_{\alpha }^{-1}:(U_{\alpha }\cap U_{\beta })\times F\stackrel{\sim }{\to }(U_{\alpha }\cap U_{\beta })\times F$ which tell us how to translate computations between our $\alpha$ and $\beta$ charts. These have to be the identity on the $U_{\alpha }\cap U_{\beta }$ part, so the interesting data is a map ${\phi }_{\beta \alpha }:F\stackrel{\sim }{\to }F$ which tells us how to glue the $\alpha$ and $\beta$ charts along their intersection.

Now if we want to answer questions corresponding to “bonus structure” on our fibre, we need to make sure we only ever glue in a way that preserves the answers to these questions. That is, instead of ${\phi }_{\beta \alpha }$ being any old diffeomorphism of $F$, we want it to be in the subgroup of diffeomorphisms respecting this structure⁹. If we call this subgroup $G$, then we call our bundle a $G$-bundle.

For example, if our fibres are all ${\mathbb{R}}^n$ and we want to ask vector-spacey questions, then we should only glue them using diffeomorphisms that respect the vector space structure. That is, we should only glue along $\mathsf{GL}(n)\subseteq \text{Diff}({\mathbb{R}}^n)$, and so we’re working with a $\mathsf{GL}(n)$-bundle. If we moreover want to ask questions about the usual inner product on ${\mathbb{R}}^n$, then we have to glue in a way that preserves the inner product so our transition functions will be valued in $\mathsf{O}(n)$¹⁰.

So it turns out the crucial data for a $G$-bundle are the transition maps ${\phi }_{\beta \alpha }:U_{\alpha }\cap U_{\beta }\to G$. These have to satisfy the Cocycle Condition¹¹ that ${\phi }_{\gamma \beta }{\phi }_{\beta \alpha }={\phi }_{\gamma \alpha }$, which crucially never mentions the fibre $F$! So we learn that $G$-bundles can be classified without referencing the fibre $F$ at all!

Indeed, say we have the data of a $G$-cocycle ${\phi }_{\beta \alpha }$. Then for any space $F$ with a $G$-action we can build a bundle with fibres $F$ by using these as our transition functions. Since we can choose any $F$ we want (at least for the purposes of classification) it’s reasonable to ask if there’s a “best” choice of fibre that makes things easier. To answer this one might ask if there’s a “best” choice of set that $G$ acts on, and from there we might be led to say that the best choice is $G$ acting on itself by multiplication!

In this case our fibres are all $G$, and it’s easy to see this preserves “relative information” about $G$ since $h^{-1}k=(gh{)}^{-1}(gk)$ and the value of $h^{-1}k$ is preserved by the multiplication action. However this action does not preserve “absolute information” about $G$, such as the identity, since $ge=g\ne e$. The structure that’s preserved is called a torsor, and so we see that any $G$-valued cocycle on $M$ naturally gives us a bundle of $G$-torsors on $M$! This is called a Principal $G$-Bundle, and from the earlier discussion if we can classify the principal $G$-bundles, we can classify all $G$-bundles easily! It turns out that in many many ways if we want to understand $G$-bundles it’s enough to understand the principal ones. For instance connections on a $G$-bundle arise in a natural way from connections on a principal $G$-bundle, and principal $G$-bundles give us a way to work with bundles in a coordinate-invariant way. I won’t say any more about this, in the interest of keeping this post quick, but I’ll point you to the excellent blog posts by Nicolas James Marks Ford¹² on $G$-bundles and connections, as well as the relevant sections of Baez and Muniain’s excellent book Gauge Fields, Knots, and Gravity.

Concretely, how can we implement this bijection?

Well, given a $G$-bundle $\pi :E\to M$ we can fix a good open cover $\{U_{\alpha }\}$ of $M$, and we can read off the transition maps ${\phi }_{\beta \alpha }:U_{\alpha }\cap U_{\beta }\to G$, and then we can build a new $G$-bundle $\tilde{E}\to M$ whose fibres are all $G$ (called the Associated Bundle to $E$) by gluing copies of $G$ together with these same transition maps ${\phi }_{\beta \alpha }$. This is a principal $G$-bundle.

In the other direction, say we have a principal $G$-bundle $\pi :P\to M$. Then if $G$ acts on any space $F$ we can build a new $G$-bundle which is fibrewise given by $E_m=(P_m\times F)/\sim$ where we quotient by the relation $(hg,f)\sim (h,gf)$. This is, in some sense, coming from the “universality” of $G$ as a $G$-set that made $G$ the “best” choice of set with a $G$-action¹³!

It’s a cute exercise to check that these operations are inverse to each other!

Now. Where did we start, and where did we end? Well we can read on wikipedia that $\mathsf{B}G$ classifies principal $G$-bundles. But we know that once we fix an action of $G$ on $F$, the principal $G$-bundles are in bijection with $G$-bundles with fibre $F$!

So using the obvious action of $\text{Diff}(F)$ on $F$, and remembering that all bundles with fibre $F$ have transition functions landing in $\text{Diff}(F)$, we get a natural bijection

$$\begin{array}{c}\{\text{homotopy classes of maps }M\to \mathsf{B}\text{Diff}(F)\}\\ ⟷\\ \{\text{principal }\text{Diff}(F)\text{ bundles on }M\}\\ ⟷\\ \{\text{bundles on }M\text{ with fibre }F\text{ whose transition maps live in }\text{Diff}(F)\}\\ ⟷\\ \{\text{all bundles on }M\text{ with fibre }F\}\end{array}$$

Which is exactly what we were looking for!

---

In hindsight, I’m not sure whether the story involving a “space of all $F$s” or the story about associated bundles is “more concrete”… I know the second story is easier to make precise, but I think both versions are good to see.

I’m super happy to have finished this post in two days. I started writing it last night when I got to my friends’ house in New York, and I finished it this morning while they were addressing and signing a bunch of christmas cards. It’s good to be thinking and writing about math again after my two months of postdoc application hell, and I’m feeling SO comfortable and relaxed it’s just great to be around people I love.

I’m going to hopefully find time to finish writing a series on skein algebras, hall algebras, and fukaya categories (which is the topic of my thesis) in the next month or two. That will be great, because I have a TON of fascinating stuff to share ^_^.

As always, thanks for hanging out. Now more than ever stay safe, stay warm, and take care of each other. Nobody else is going to.

Also… wow I’m tall.

---