Some Doodles I'm Proud of -- The Capping Algorithm for Embedded Graphs

30 Mar 2025 - Tags: pretty-pictures

This will be a really quick one! Over the last two weeks I’ve been finishing up a big project to make DOIs for all the papers published in TAC, and my code takes a while to run. So while testing I would hit “go” and have like 10 minutes to kill… which means it’s time to start answering questions on mse again! I haven’t been very active recently because I’ve been spending a lot of time on research and music, but it’s been nice to get back into it. I’m especially proud of a few recent answers, so I think I might quickly turn them into blog posts like I did in the old days! In this post, we’ll try to understand the Capping Algorithm which turns a graph embedded in a surface into a particularly nice embedding where the graph cuts the surface into disks. I drew some pretty pictures to explain what’s going on, and I’m really pleased with how they turned out!

So, to start, what’s this “capping algorithm” all about?

Say you have a (finite) graph $G$ and you want to know what surfaces it embeds into. For instance planar graphs are those which embed in $\mathbb{R}^2$ (equivalently $S^2$), and owners of this novelty mug know that even the famously nonplanar $K_{3,3}$ embeds in a torus¹:

Obviously every graph embeds into some high genus surface – just add an extra handle for every edge of the graph, and the edges can’t possibly cross each other! Also once you can embed in some surface you can obviously embed in higher genus surfaces by just adding handles you don’t use.

This leads to two obvious “extremal” questions:

1. What is the smallest genus surface which $G$ embeds into?
2. What is the largest genus surface which $G$ embeds into where all the handles are necessary?

Note we can check if a handle is “necessary” or not by cutting our surface along the edges of our graph. If the handle doesn’t get cut apart then our graph $G$ must not have used it! This leads to the precise definition:

Then the “largest genus surface where all the handles are necessary” amounts to looking for the largest genus surface where $G$ admits a 2-cell embedding! But in fact, we can restrict attention to 2-cell embeddings in the smallest genus case too, since if we randomly embed $G$ into a surface, there’s an algorithm which only ever decreases the genus and outputs a 2-cell embedding! So if $S$ is the minimal genus surface that $G$ embeds in, we can run this algorithm to get a 2-cell embedding of $G$ in $S$.

And what is that algorithm? It’s called Capping, see for instance Minimal Embeddings and the Genus of a Graph by J.W.T. Youngs. The idea is to cut your surface along $G$, look for anything that isn’t a disk, and “cap it off” to make it a disk. Then you repeat until everything in a disk, and you stop.

The other day somebody on mse asked about this algorithm, and I had a lot of fun drawing some pictures to show what’s going on²! This post basically exists because I was really proud of how these drawings turned out, and wanted to share them somewhere more permanent, haha.

Anyways, on with the show!

---

We’ll start with an embedding of a graph 𝐺 (shown in purple) in a genus 2 surface:

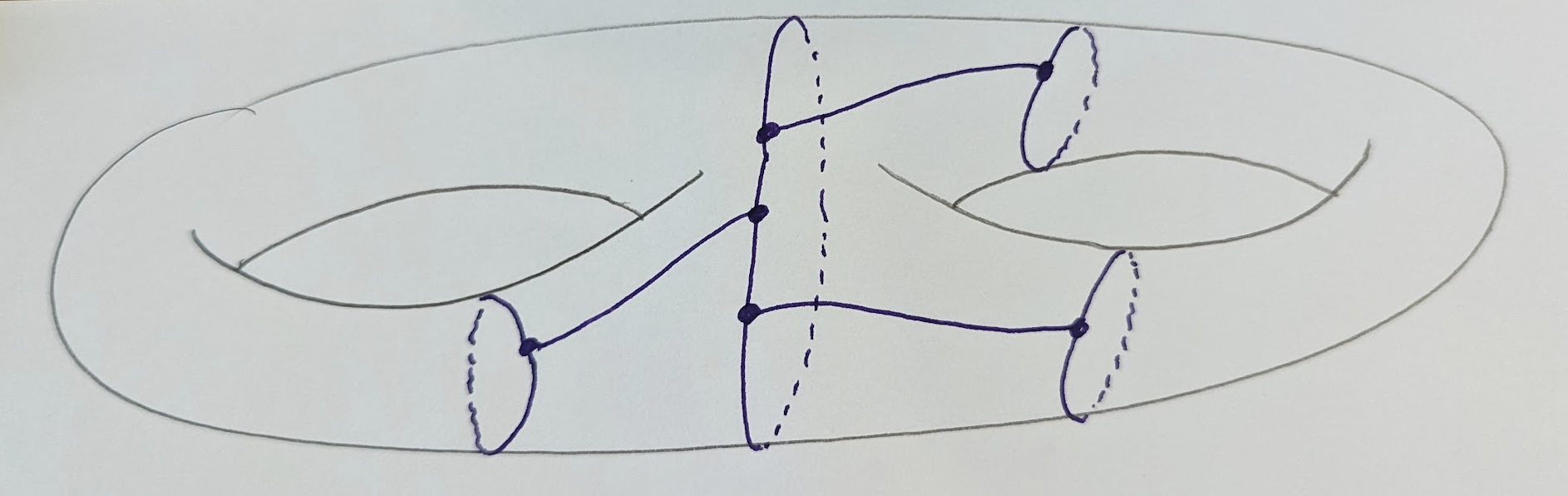
we’ll cut it into pieces along $G$, and choose one of our non-disk pieces (call it $S$) to futz with:

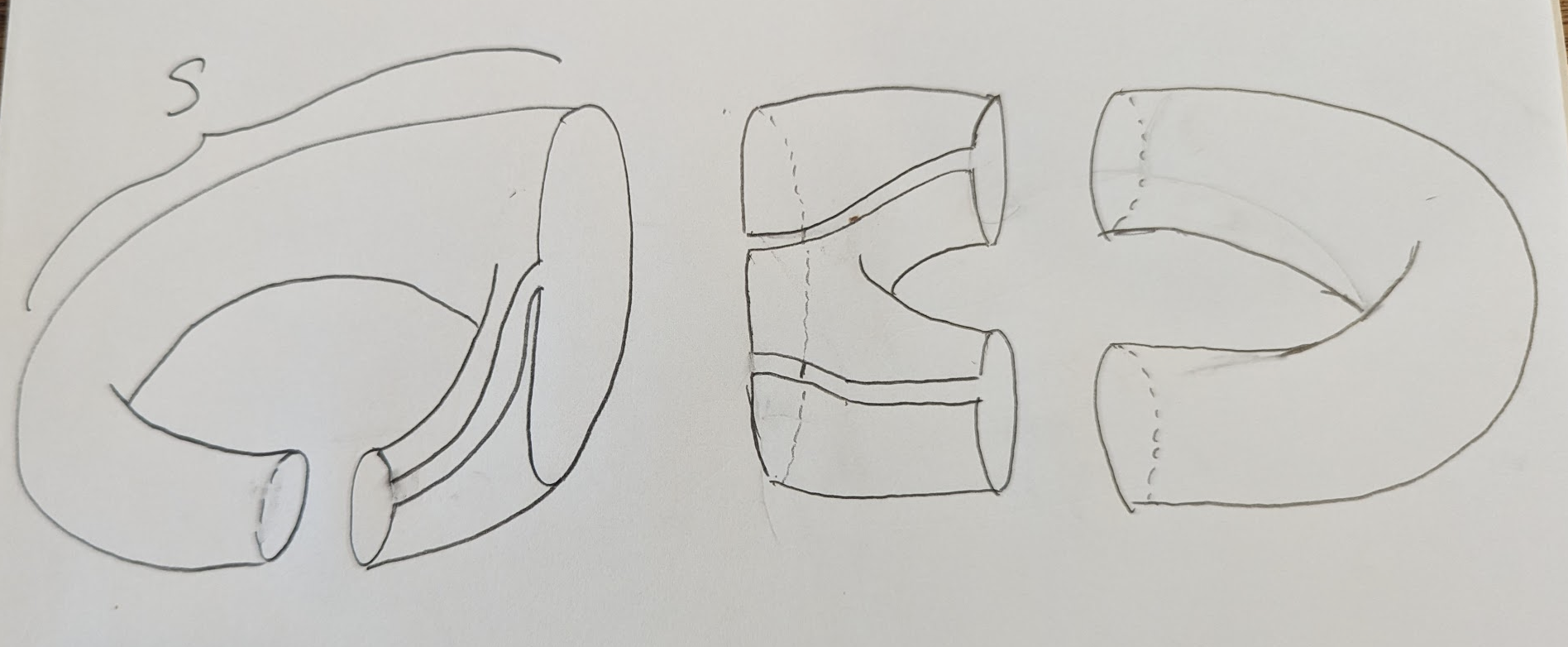
Now we choose³ a big submanifold $T \subseteq S$ which leaves behind cylinders when we remove it. Pay attention to the boundary components of $T$, called $J_1$ and $J_2$ below, since that’s where we’ll attach a disk to “cap off” where $T$ used to be

We glue all our pieces back together, but remove the interior of $T$

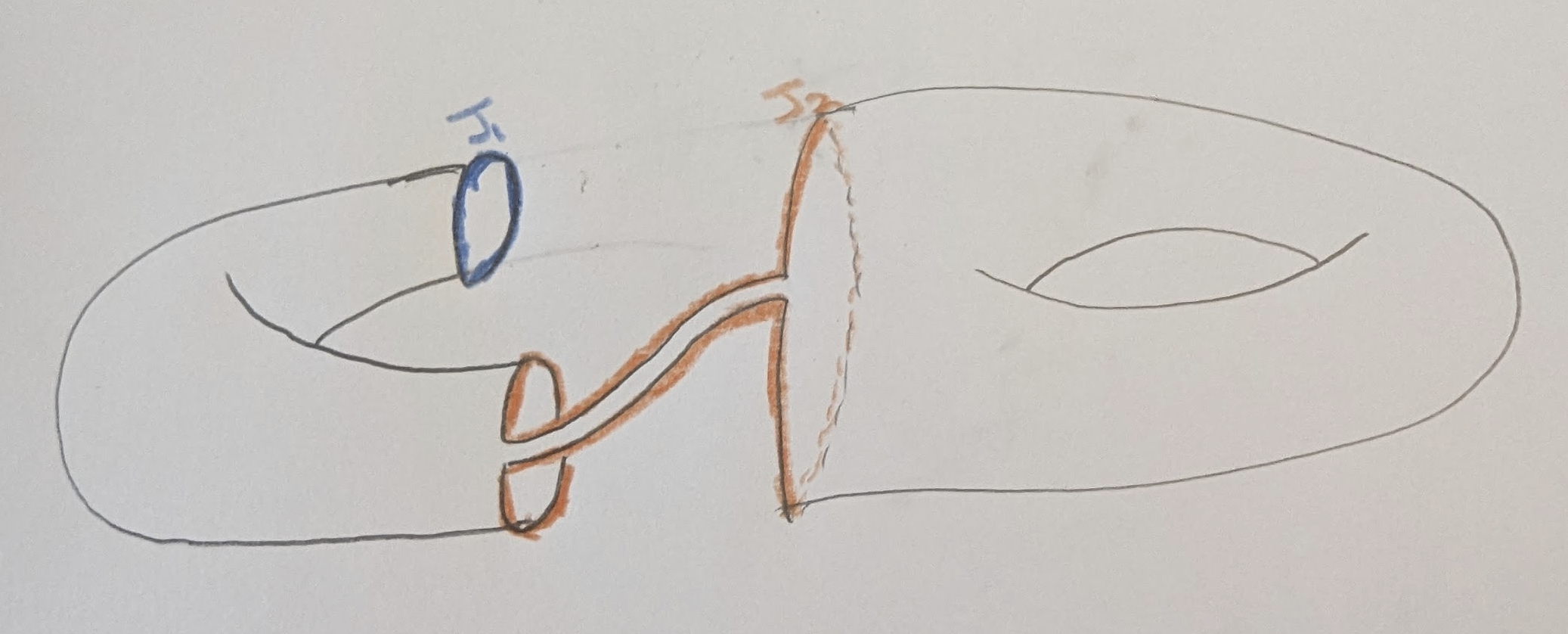
and then, as promised “cap off” the boundary components $J_1$ and $J_2$ with disks. Note that the genus decreased when we did this! It used to be genus 2, and now we’re genus 1!

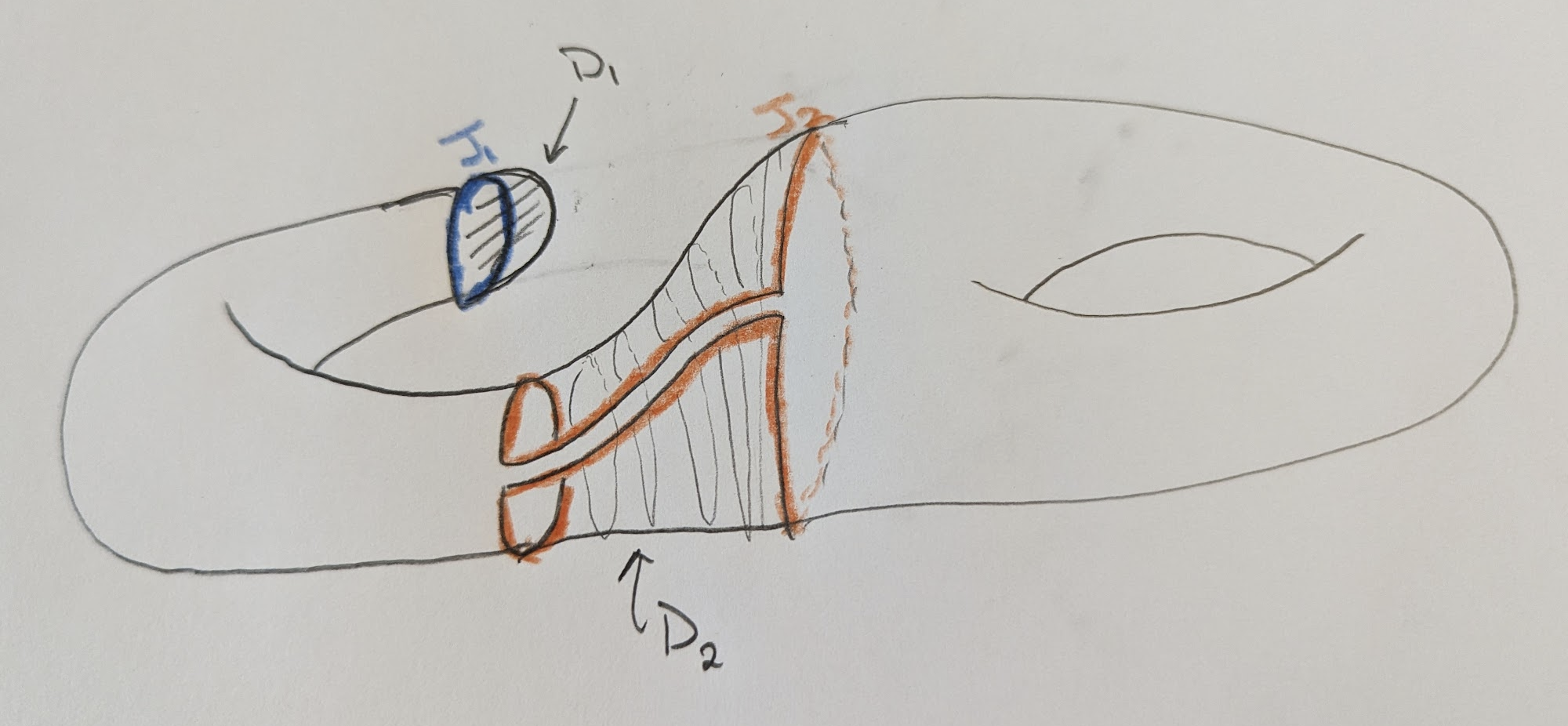
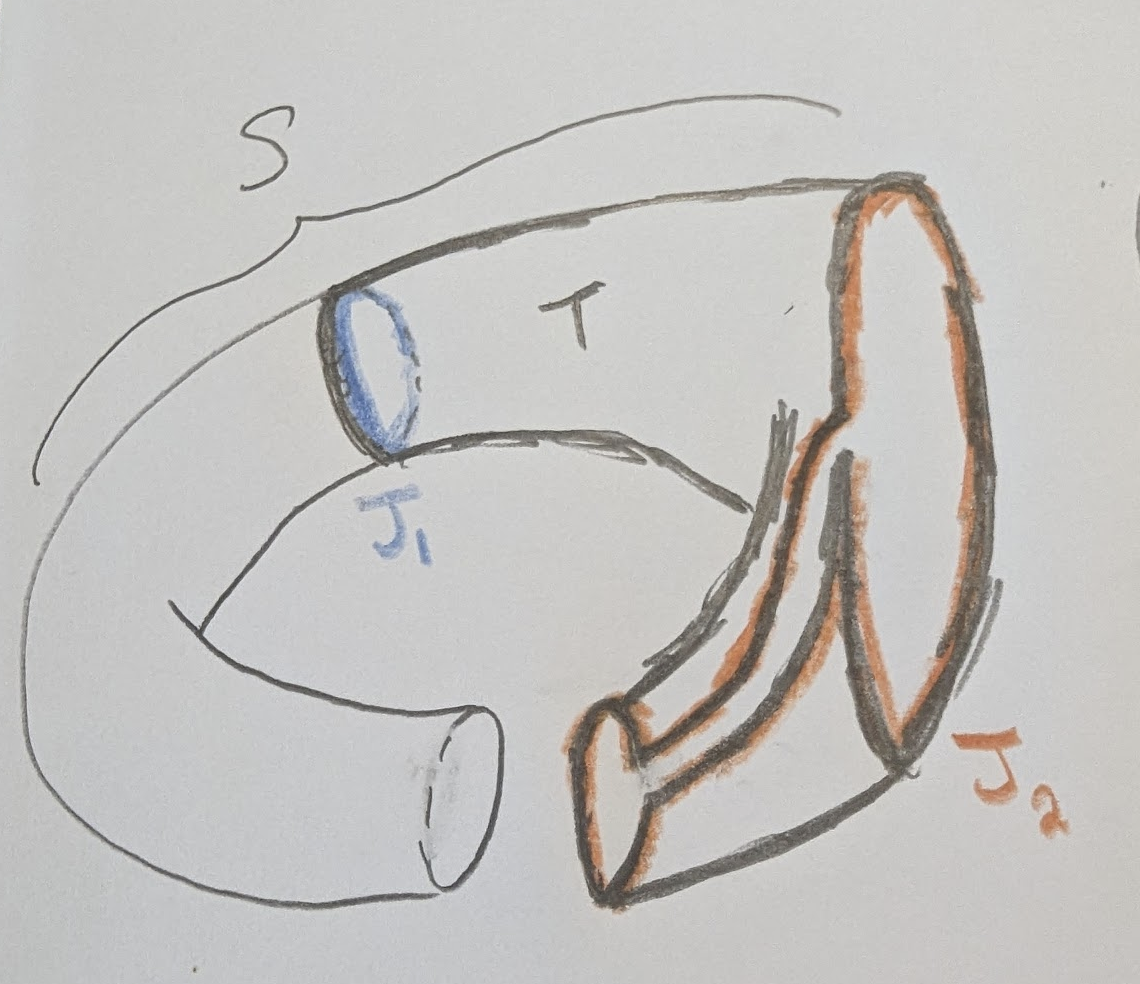
Note also that $G$ still embeds into our new surface:

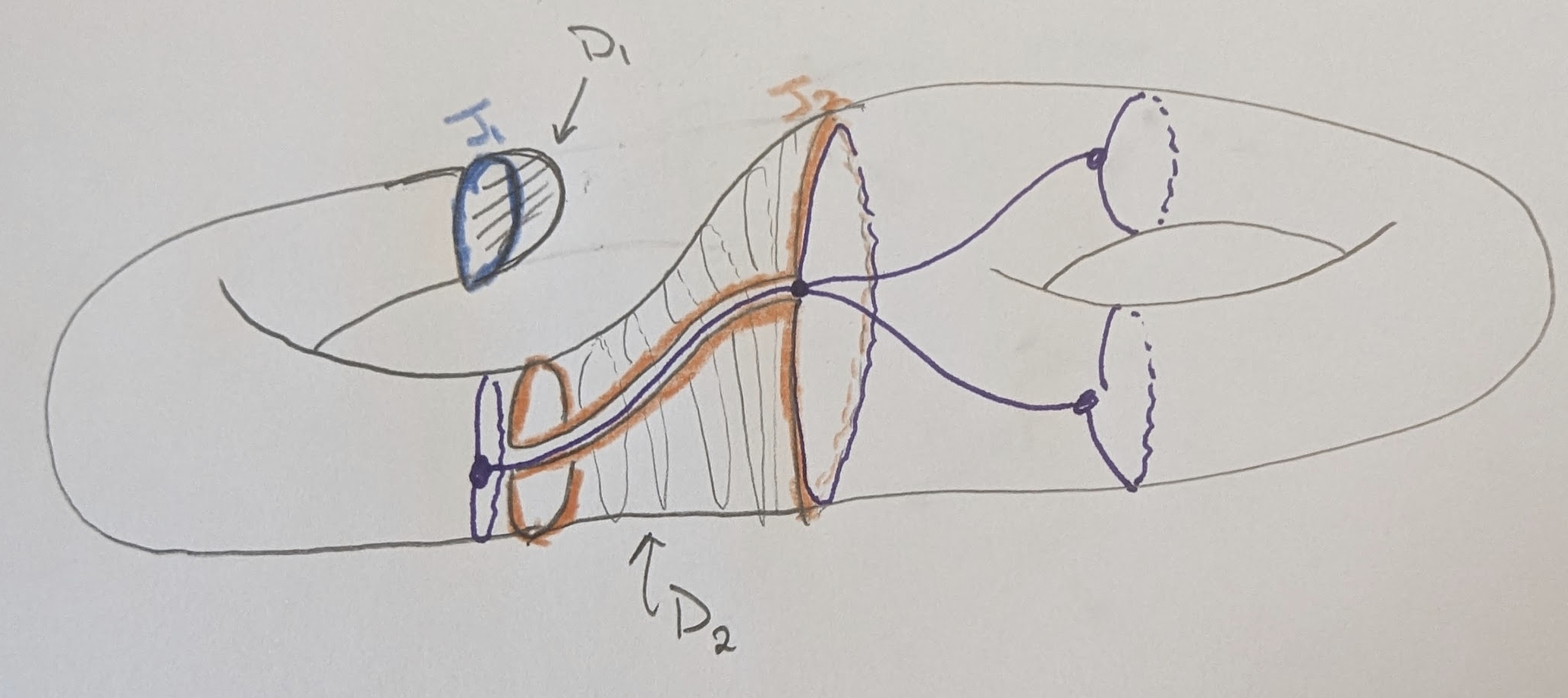
Let’s squish it around to a homeomorphic picture, then do the same process a second time! But faster now that we know what’s going on:

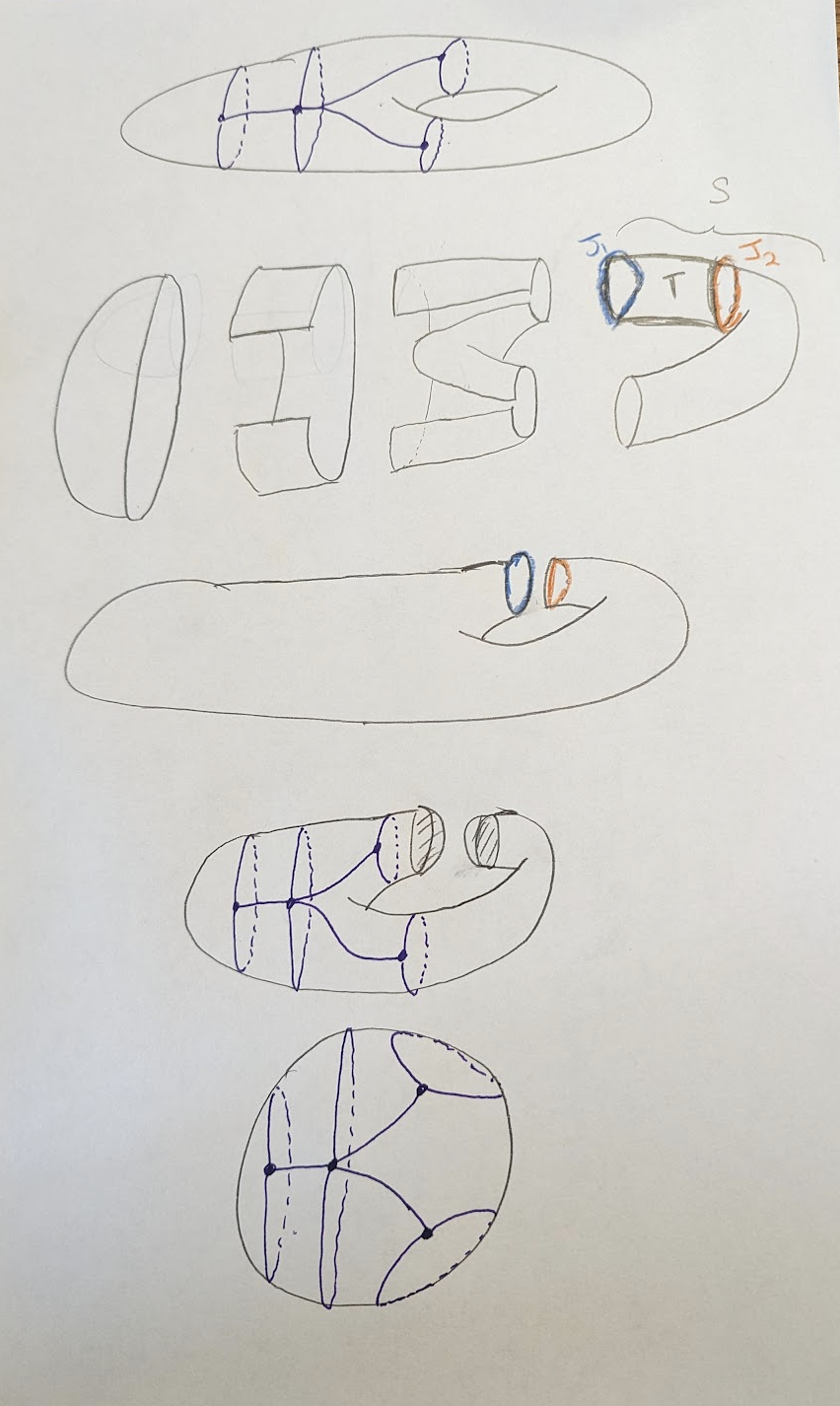
At this point, we can try to do it again, but we’ll find that removing $G$ cuts our surface into disks:

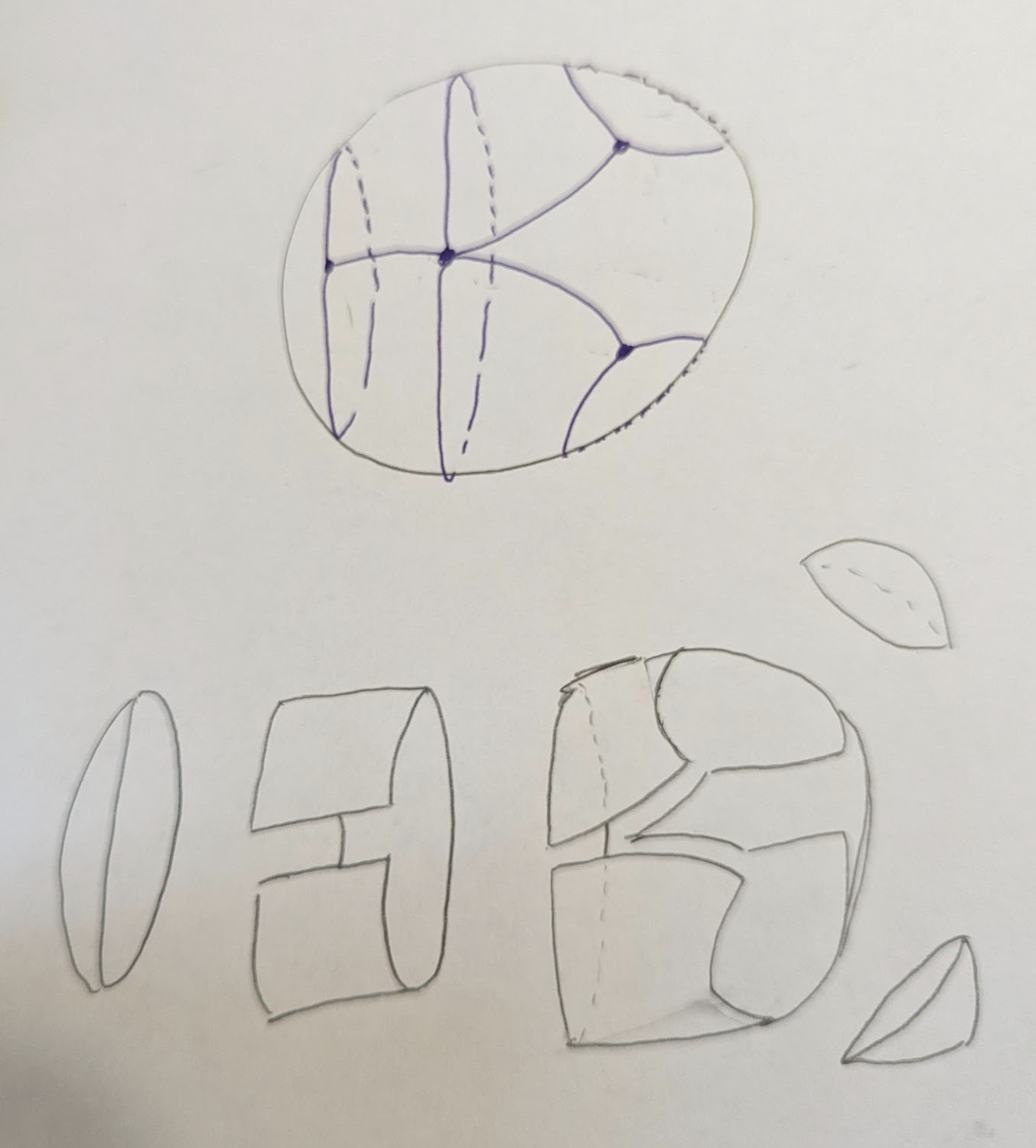
This tells us the algorithm is done, since we’ve successfully produced a 2-cell embedding of $G$ ^_^.

---

Wow that was a really quick one today! Start to finish in under an hour, but it makes sense since I’d already drawn the pictures and spent some time doing research for my answer the other day. Maybe I’ll go play flute for a bit.

Thanks for hanging out, all! Stay safe, and see you soon ^_^

---