How to Explicitly Compute Charts for a Levelset Submanifold
20 Jun 2025
While doing a computation with my friend Shane the other day,
we realized we needed to explicitly compute a local chart near the
identity of
Ok, let’s hop right in! Say you have a
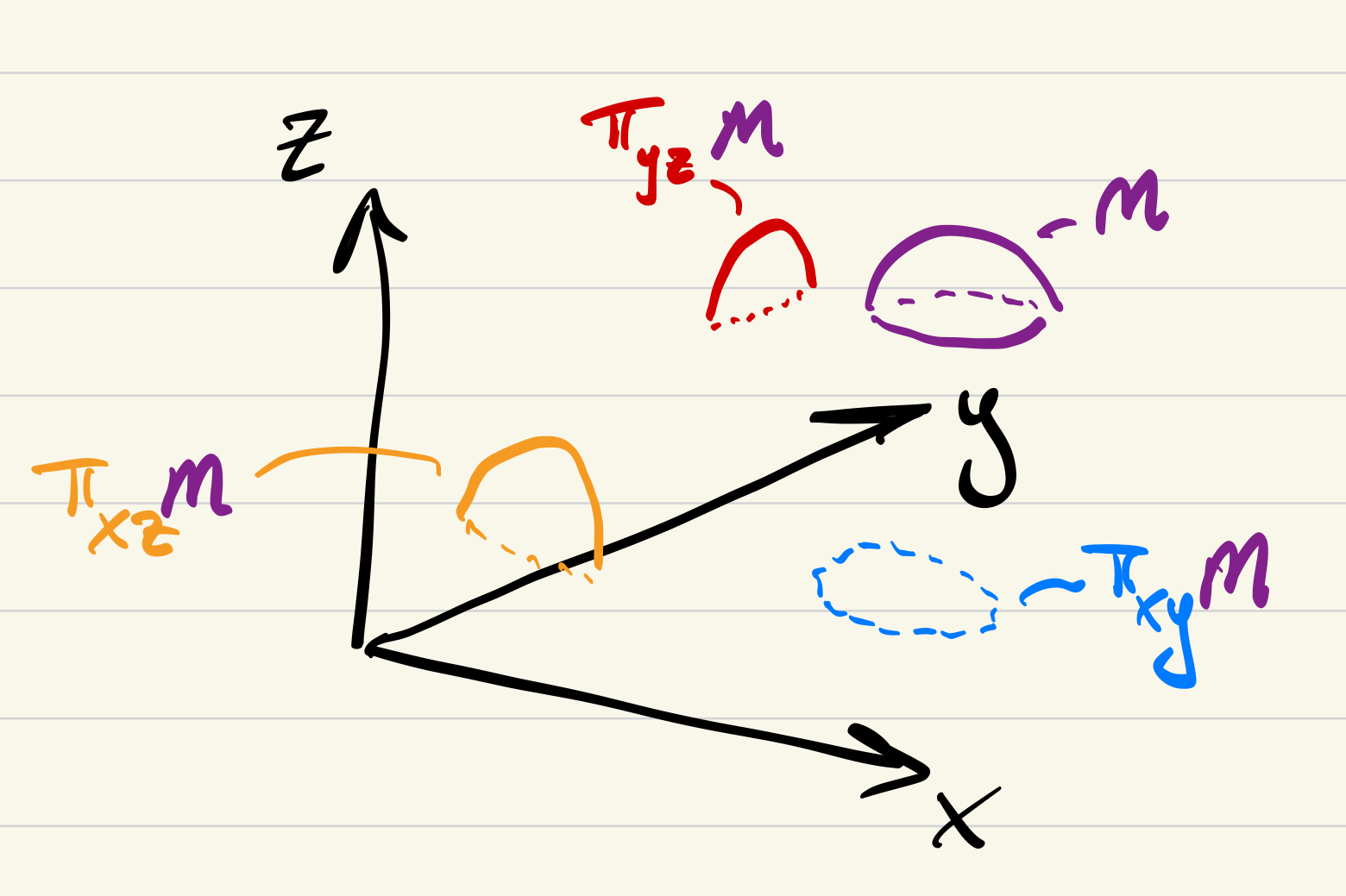
If we think of the purple manifold
For a more computational example, let’s try the hyperboloid
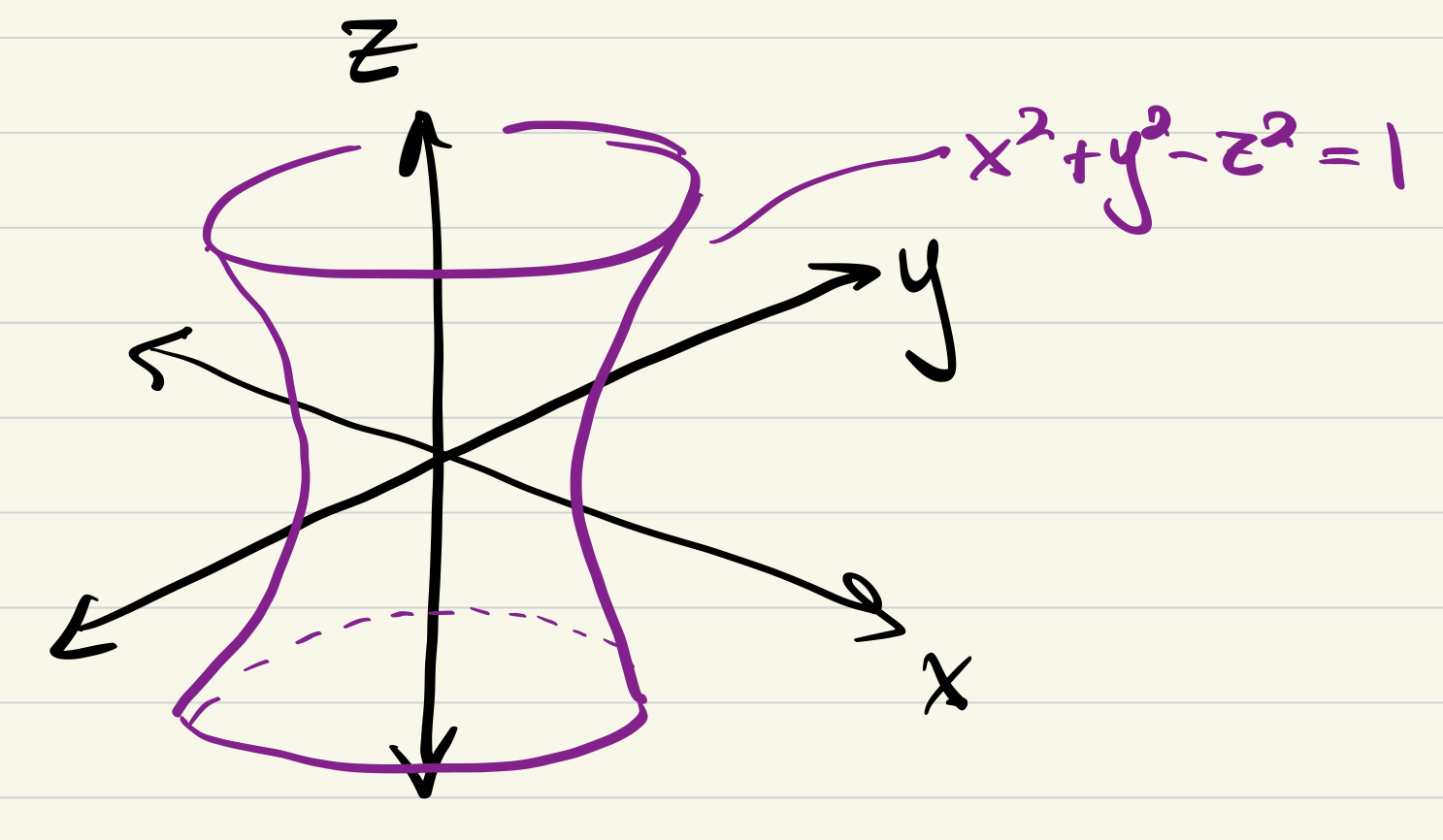
The tangent plane at a point is controlled by the jacobian of the
defining equation, which for us is
This gives us three (disconnected) charts:

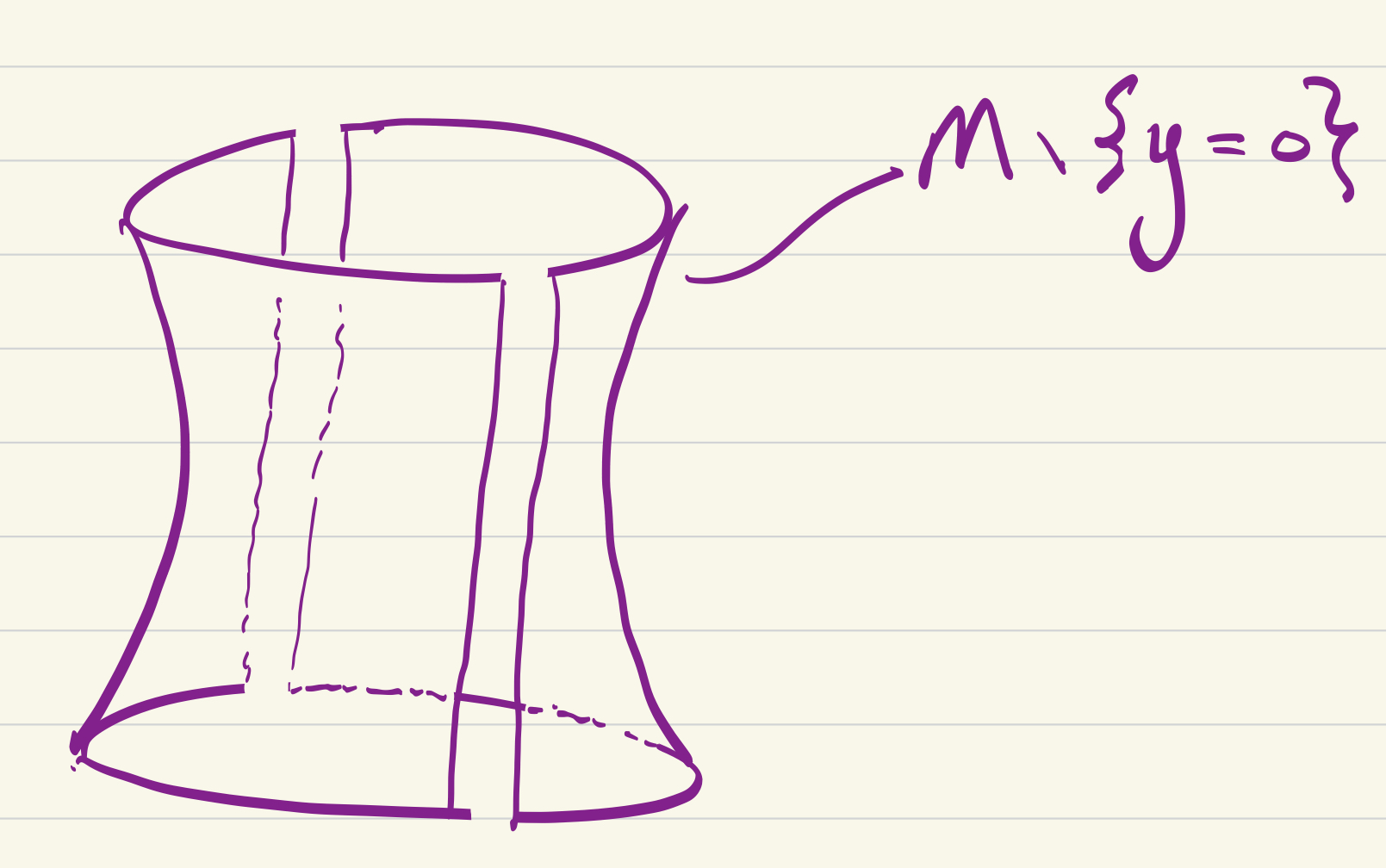
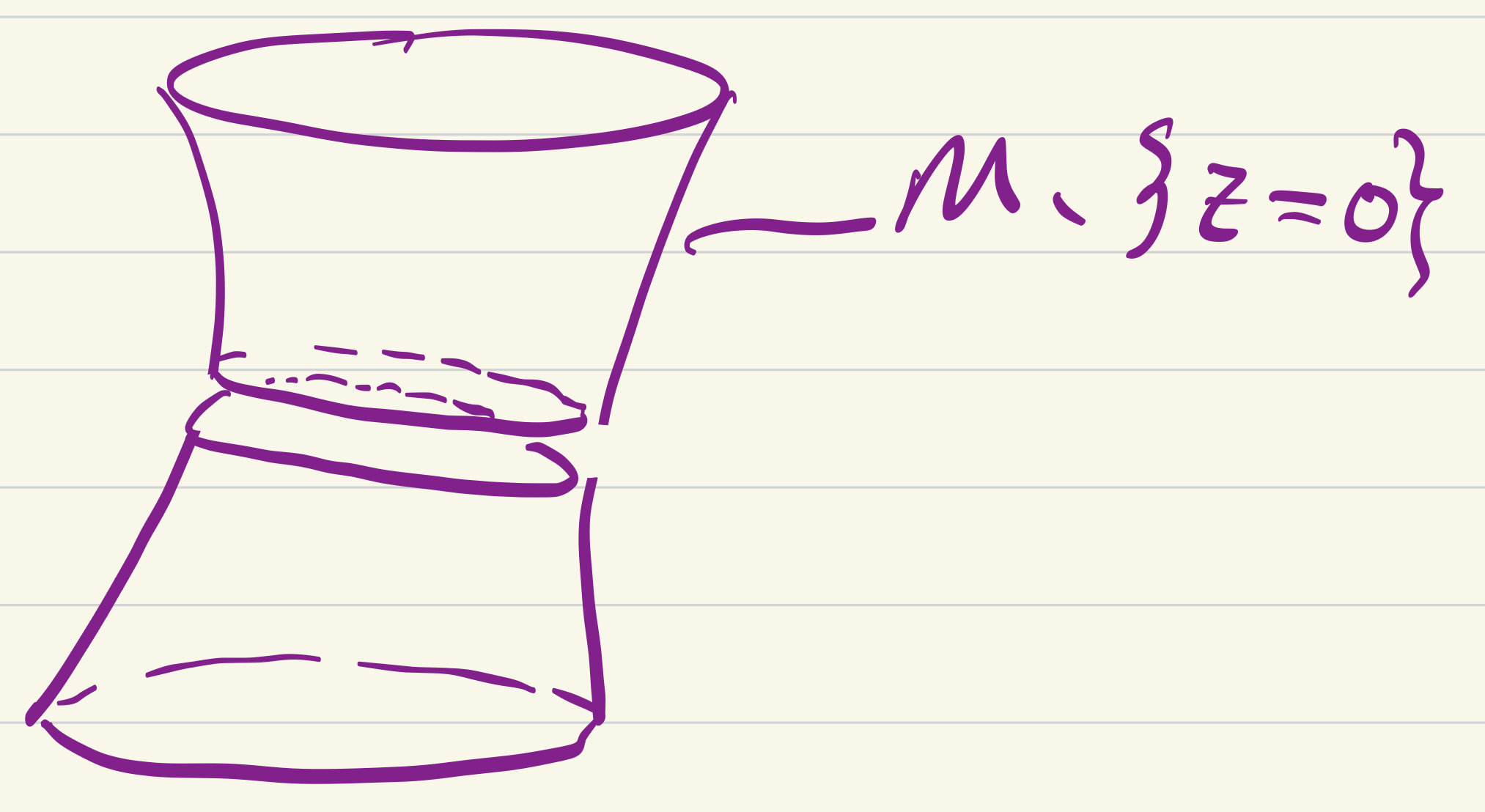
These turn into 6 honest-to-goodness charts where we turn the disconnected
condition
On
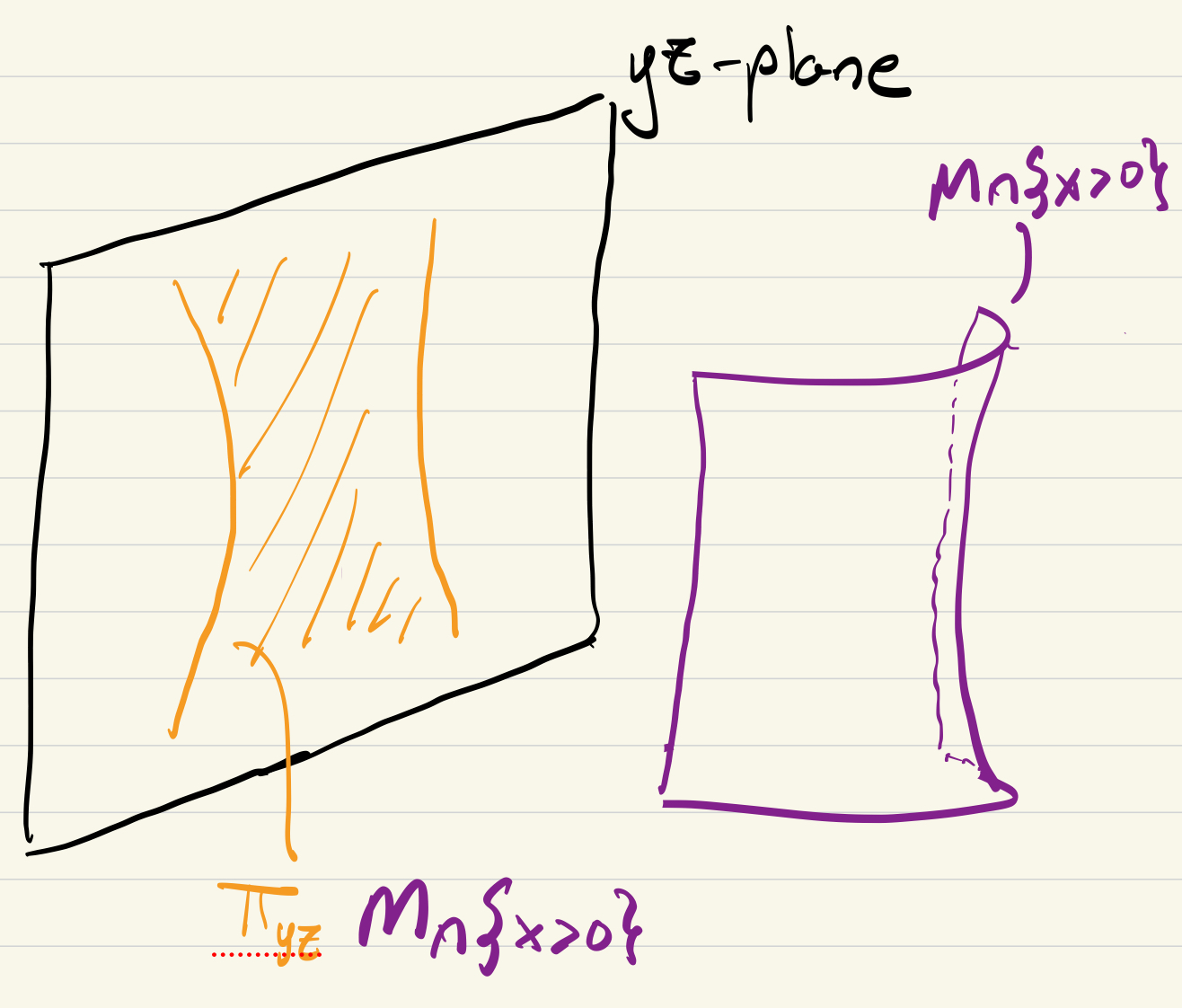
Algebraically, we compute this chart by noting on
which is diffeomorphic in the obvious way to its projection onto the
so this is one of our charts!
Similarly, we can look at
which is diffeomorphic to
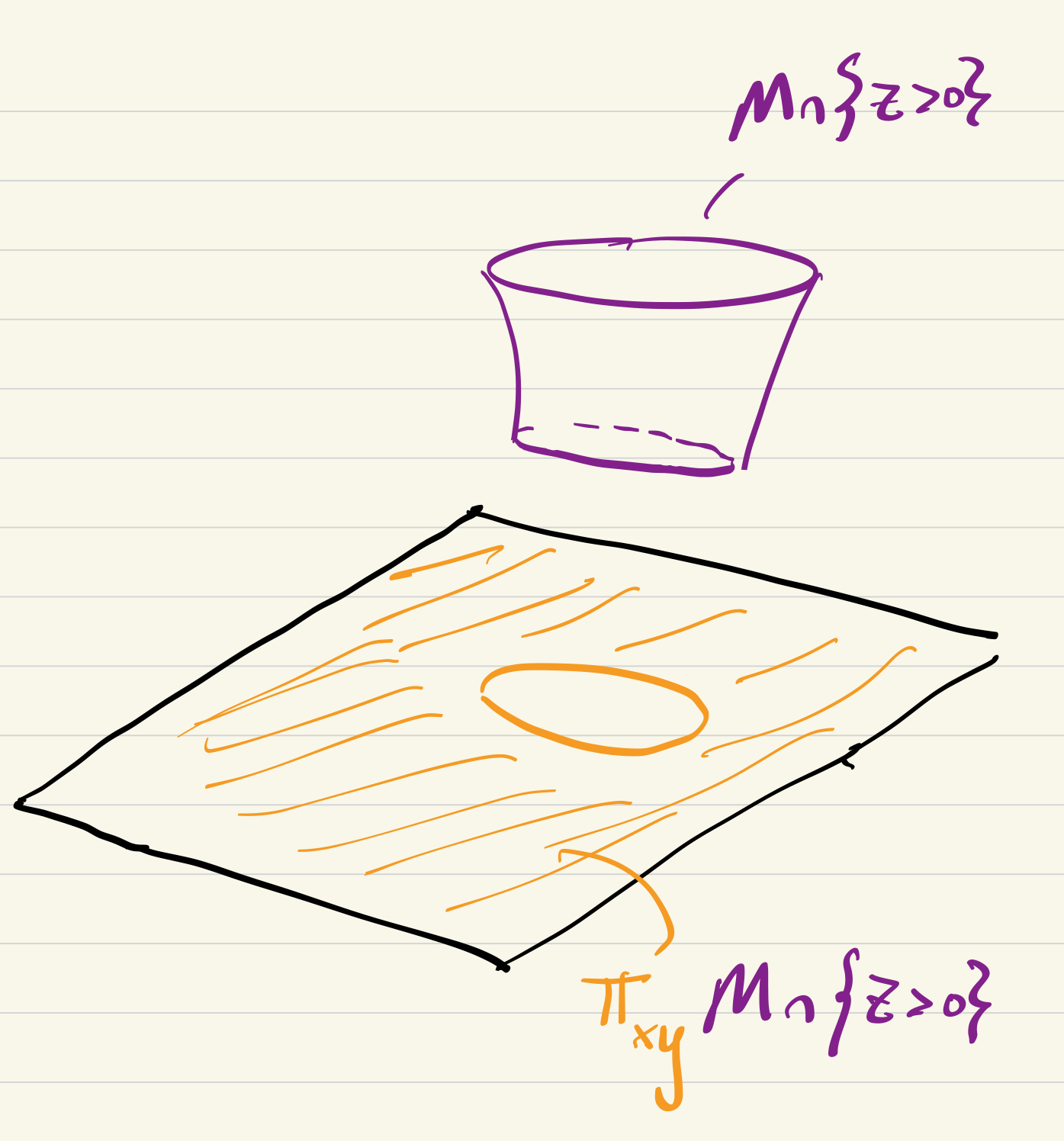
On the intersection of these charts,
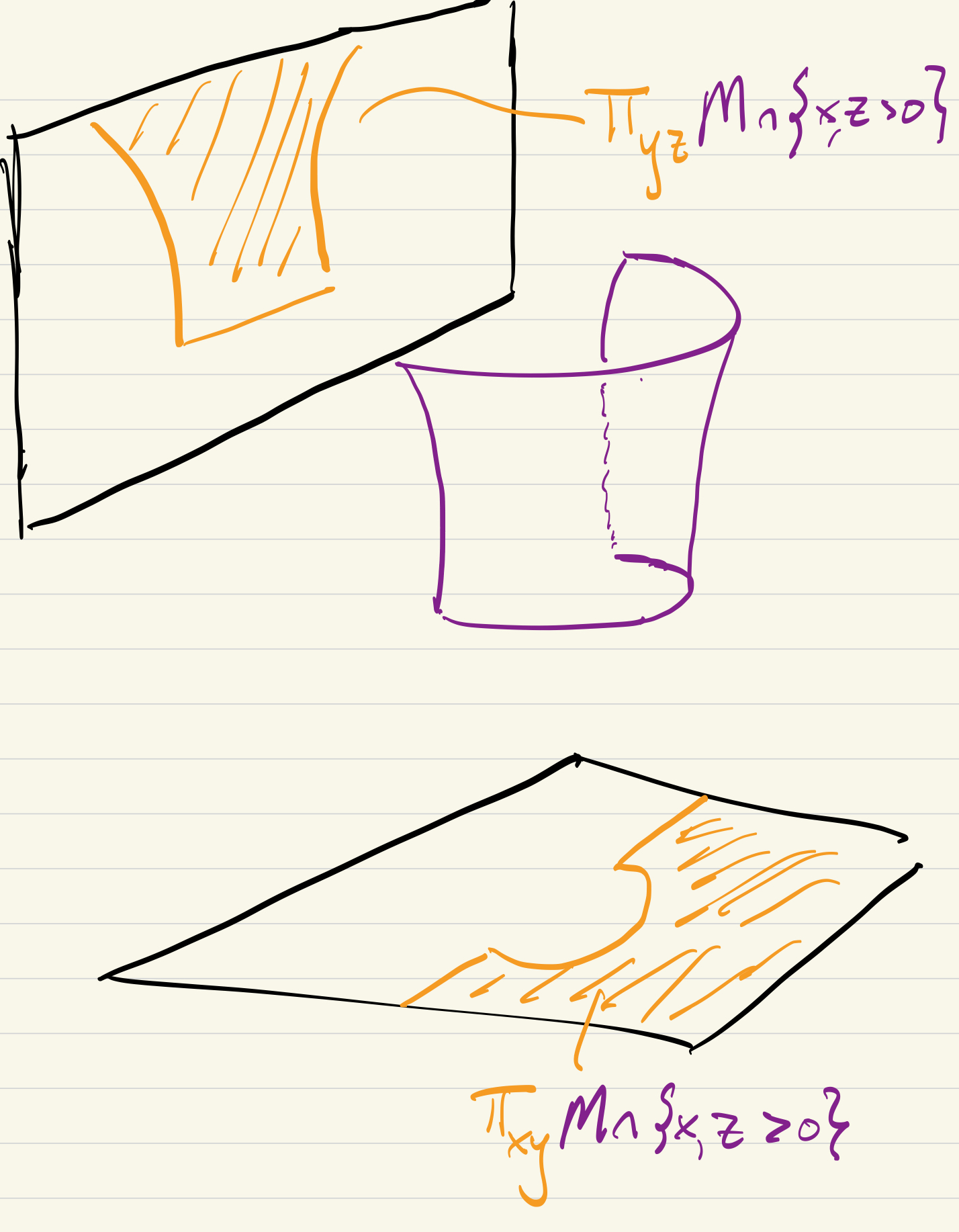
Here our charts are the diffeomorphisms
so it’s easy to compose them to see our transition maps between these charts are
As a (fun?) exercise, compute the
For another example, let’s take a look at
Then the jacobian of our defining map is
In the
In the main post you can see how my friend Shane and I used this to compute the anchor map for a certain lie algebroid.
Again, it makes a nice exercise to explicitly write out the various charts and transition maps
What about a codimension 2 example?
Let’s go back to our happy little hyperboloid, and intersect it
with the surface
This is the levelset of the map
and our charts are all the ways this matrix can have full rank. These conditions are:
If we look at the
xxxxxxxxxxx,y,z = var('x,y,z')solns = solve([x^2 + y^2 + z^2 == 1, x*y*z == 1], [x,z])for soln in solns: show(soln)So as in the previous hyperboloid example, we need to break this
into four charts, depending on whether
Following the sage computation, in the
which, by projecting out the
Ok, thanks for reading, all! This was extremely instructive for me, and hopefully it’s helpful to some of you as well! Sometimes it’s nice to just do some computations. Talk soon!