Chain Homotopies Geometrically

24 Jun 2022

The definition of a Chain Homotopy has always felt a bit weird to me. Like I know that it works, but nobody made it clear to me why it worked. Well, the other night I was rereading part of Aluffi’s excellent Algebra: Chapter 0, and I found a picture that totally changed my life! In this post, we’ll talk about two ways of looking at chain homotopies that make them feel more like their topological namesake.

(As an aside, I was reading through Aluffi because I’ve been thinking a lot about derived categories lately, and I wanted to see how he motivated them in an introductory algebra book. I’ll be coming out with a blog post¹, hopefully quite soon, where I talk about model categories and their close friends $\infty$-categories. It’s been easily my hardest ever post to write, but I think it’s almost ready! So get excited ^_^)

I want this to be a genuinely quick post, so I’ll be assuming some familiarity with algebraic topology, mainly homology and chain complexes. As a quick refresher, though:

A Chain Complex of abelian groups is a sequence

\[\cdots \overset{\partial_{n+1}}{\to} A_n \overset{\partial_n}{\to} A_{n_1} \overset{\partial_{n-1}}{\to} A_{n-2} \overset{\partial_{n-2}}{\to} \cdots\]

so that $\partial_{n-1} \circ \partial_n = 0$ for all $n$.

We’ll refer to the entire complex by $A_\bullet$, and we’ll (abusively) suppress the indices of the “boundary maps” $\partial_n$, calling them all $\partial$².

In this notation, the chain condition is that $\partial^2 = 0$.

These first arose in topology. For instance, in order to study the (singular) homology of a topological space $X$, we build a chain of abelian groups

\[\cdots \to C_{n+1}(X) \to C_n(X) \to C_{n_1}(X) \to \cdots\]

where $C_n(X)$ is the free abelian group on the set of maps from the $n$-simplex into $X$ (and is $0$ for negative $n$), and if $\sigma : \Delta^{n+1} \to X$, then $\partial \sigma$ is the (alternating) sum of the $\sigma \restriction \Delta^n_i$, where $\Delta^n_i$ is the $i$th face of the simplex.

Then the Homology Groups of $X$ are defined to be

\[H_n(X) \triangleq \text{ker}(\partial_n) \big / \text{im}(\partial_{n+1})\]

I won’t says any more about this here, but if you’re interested you should read my old post on cohomology³. What matters is that this “boundary operator” literally comes from the boundary of a geometric object!

I also won’t try to motivate chain complexes in this post⁴. It turns out they’re extremely useful algebraic gadgets, and show up naturally in every branch of modern geometry, as well as in “pure” algebra such as group theory, module theory, representation theory, etc. Chain complexes are ubiquitious in math nowadays, and if you haven’t met them yet, you’ll surely meet them soon!

Motivation aside, what matters is that this construction is functorial, and so a map $f : X \to Y$ induces a “chain map” $C_\bullet f : C_\bullet(X) \to C_\bullet(Y)$, where $C_n f : C_n(X) \to C_n(Y)$ is the map that sends

\[(\sigma : \Delta^n \to X) \mapsto (f \circ \sigma : \Delta^n \to Y)\]

Moreover, it’s not hard to check that this $C_n f$ is well defined on homology classes, so descends to a map $H_n f : H_n(X) \to H_n(Y)$.

Next, topologically we have a notion of “homotopy”:

We say that two maps $f, g : X \to Y$ are Homotopic if there is a map $H : X \times [0,1] \to Y$ (the homotopy from $f$ to $g$) so that

$H(x,0) = f(x)$
$H(x,1) = g(x)$

We think of $H(x_0,t)$ as giving a path in $Y$ from $f(x_0)$ to $g(x_0)$, so that we can “smoothly deform” $f$ into $g$.

For geometric reasons, we expect that two homotopic maps $f$ and $g$ should induce the same map on homology⁵, so we would like a way of translating the homotopy $H$ into an algebraic object.

Enter the chain homotopy!

Say $f$ and $g$ are two chain maps $A_\bullet \to B_\bullet$.

A Chain Homotopy $H$ from $f$ to $g$ is a series of maps $H_n : A_n \to B_{n+1}$ so that⁶

$f - g = \partial H + H \partial$

At this point I’m legally required to show the following diagram:

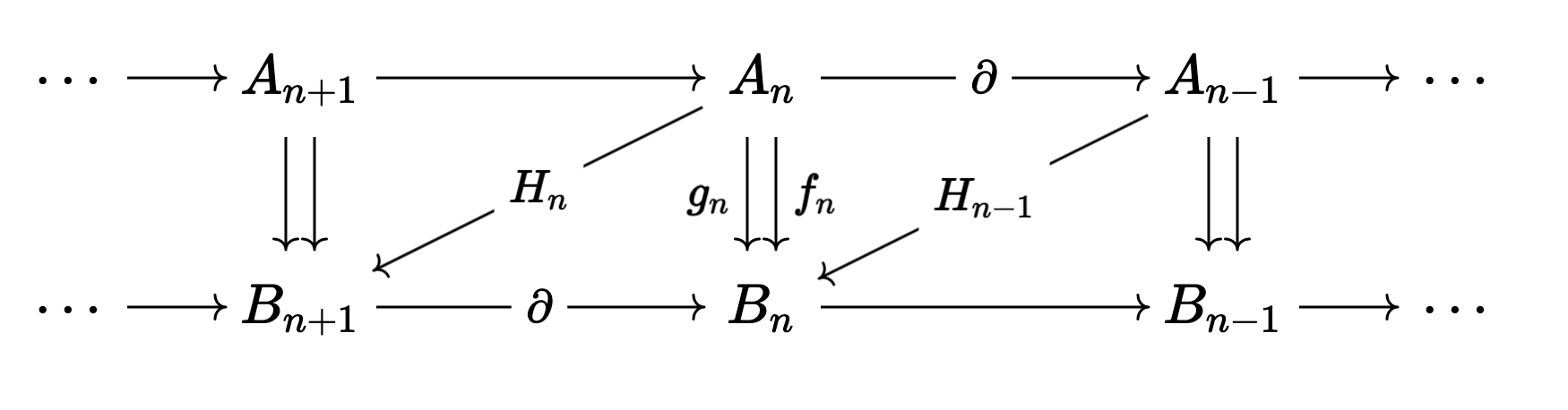
Now it’s a theorem that two chain homotopic maps induce the same maps on homology. It’s then pretty easy to show that if $f, g : X \to Y$ are homotopic (witnessed by a homotopy $H$), then the map $C_\bullet f$ and $C_\bullet g$ are chain homotopic (witnessed by a chain homotopy that we can build from $H$).

So this all works… but this condition has always seemed a bit odd to me. Where is this definition of chain homotopy coming from? It must be some translation from the topological notion of homotopy into the algebraic world… But how?

Let’s find out!

The first approach is the one that inspired me to write this post. You can read the original on page $611$ of Aluffi’s Algebra: Chapter 0. In case a new edition comes out, this is Section IX.4.3.

As an homage, let’s steal Aluffi’s diagram:

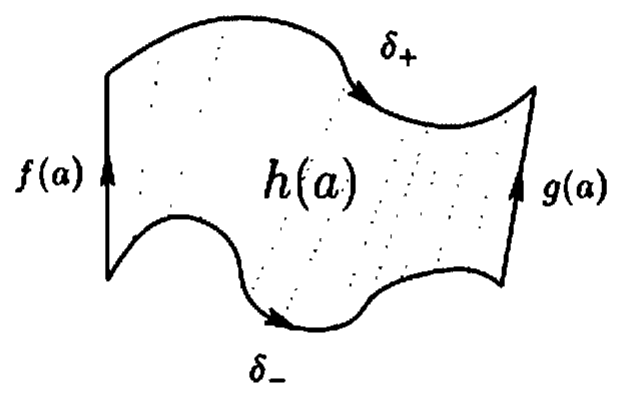
Let $a$ be an $n$-chain in $X$. Since high dimensions are hard to draw, we picture it as a $1$-chain. That is, as a path in $X$.

Then $f(a)$ (formally $f \circ a$) is the $1$-chain in $Y$ shown on the left of the diagram. Similarly $g(a)$ is the $1$-chain on the right of the diagram. Now $H : X \times [0,1] \to Y$, so $H(a,t)$ is a map from $\Delta^1 \times [0,1] \to Y$, that is, from the square into $Y$. Aluffi is calling this $h(a)$, and it’s the “filled in” $2D$ square that we see⁷.

Now for the magic! Let’s look at the boundary of $h(a)$. This is given by the (oriented) sum of the four sides of our square. So if we read counterclockwise starting at the bottom right, we see

\[\partial h(a) = g(a) - \delta_+ - f(a) + \delta_-\]

But what is $\delta_+ - \delta_-$? Well, a moment’s thought shows that it’s $h(\partial a)$! After all, since $a$ is a path in $X$, $\partial a$ is just the endpoints of the path. So $h(\partial a)$ is $h$ applied to the endpoints of $a$. That is, it’s the paths in $Y$ connecting $f(\partial a)$ to $g(\partial a)$, and these are exactly $\delta_+$ and $\delta_-$.

So then

\[\partial h(a) = g(a) - f(a) - h(\partial a)\]

\[g - f = \partial h + h \partial\]

which we recognize as the definition of a chain homotopy!

There’s another, more conceptual, way to relate the notion of a chain homotopy to the classical topological notion of a homotopy. This time, we’ll go through the machinery of a model category.

Now, if I didn’t want to motivate homology in this post, I certainly don’t want to motivate model categories! Or even define them for that matter. I fully expect this material to be less approachable than what came before, but that’s not so big a deal⁸. To quote Eisenbud:

You should think of [this] as something to return to when more of the pieces in the vast puzzle of mathematics have fallen into place for you.

Now, remember what a homotopy was in topology. If $f,g : X \to Y$, then a homotopy is a map $H : X \times [0,1] \to Y$ so that $H(x,0) = f(x)$ and $H(x,1) = g(x)$.

Is there a way to directly imitate this definition in the category of chain complexes? Surprisingly, the answer is yes!

What about the interval $[0,1]$ is really useful for this definition? Well, obviously it has two special points $0$ and $1$. But moreover, it’s contractible, so it’s equivalent to a point itself. This is best made precise through the language of model categories (or better, $\infty$-categories) but we can find an object in the category of chains which plays the same role!

How do we do it? Well, let’s build the (simplicial) chain complex of the interval!

We have two $0$-cells, so $C_0 = \mathbb{Z}^2$. Then we have one $1$-cell connecting them, so $C_1 = \mathbb{Z}$. Then a moment’s thought about the orientation shows that the boundary map should be

\[\begin{align} \mathbb{Z} &\overset{\partial}{\to} \mathbb{Z}^2 \\ 1 &\mapsto (1,-1) \end{align}\]

So we can think of this chain complex (with $0$s going off to the left and right) as a kind of “interval object” inside the category of chains⁹. With that in mind, let’s call it $I_\bullet$.

Now, if we have two maps $f,g : A_\bullet \to B_\bullet$, what’s the most natural way to build a homotopy $H$ from $f$ to $g$? Well, imitating topology, we should look at¹⁰

\[H : A_\bullet \otimes I_\bullet \to B_\bullet\]

Now here’s a fun (only slightly tricky) exercise¹¹:

$H : A_\bullet \to B_{\bullet + 1}$ is a chain homotopy from $f$ to $g$ if and only if

\[(H,f,g) : A_\bullet \otimes I_\bullet \to B_\bullet\]

makes the following diagram commute

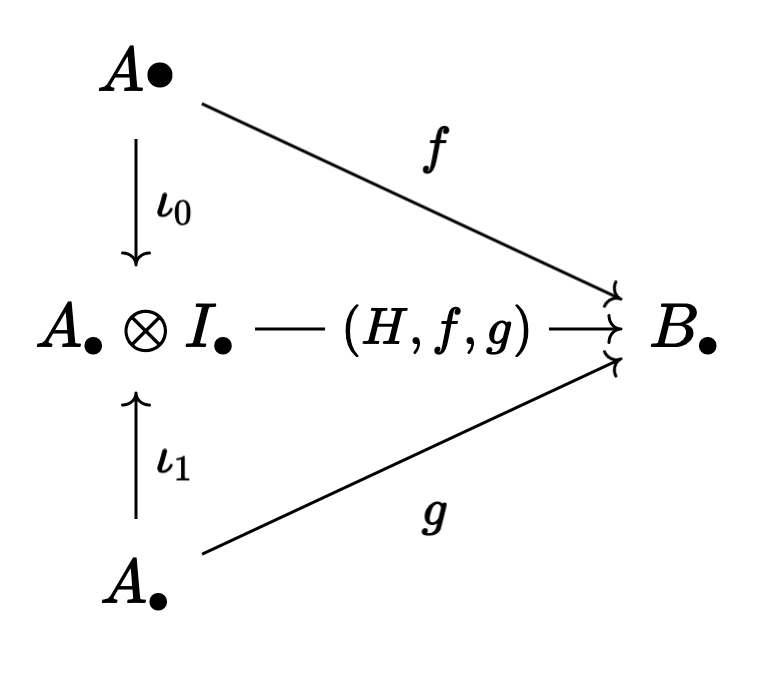
Honestly, it’s a good enough exercise to just construct $\iota_0$ and $\iota_1$, plus check that $(H,f,g)$ really does define a map from $A_\bullet \otimes I_\bullet \to B_\bullet$.

If you get stuck, you can find a proof in proposition 3.2 here

I’ve been working with chain homotopies for years now, and out of familiarity I’d stopped wondering what the definition really meant. Pragmatically this was probably good for me, but I remember in my first algebraic topology class being horribly confused by the origins of this definition, and I’m glad that I finally figured out how this definition relates to the underlying geometry! Hopefully you found this helpful too if you’re still early in your time learning about chain homotopies. To me, this makes the definition feel much more natural.

Now, though, it’s time for bed. Take care, all, and I’ll see you soon ^_^

Really a trilogy of blog posts… There’s a reason it’s taking so long. ↩
Believe me, I sympathize if you’re new to the subject. It gets worse, we often use $\partial$ to be the boundary maps (also called differentials) for different complexes! Indeed, this is exactly the convention I’ll take later in this post.

Thankfully, with experience you get used to this, and in the short term there’s always a unique way to assign any fixed $\partial$ you happen to see a “type” so that the entire expression typechecks ↩
Wow… I sure did say I would write a sequal to this post… Over a year ago…

I’ll get to it one day, haha. ↩
After working on the model category and $\infty$-category posts for so long, I really want to write a quick post, haha. My goal is to get this whole thing written in less than an hour. ↩
If $X$ is a manifold, then we think of elements of $H_n(X)$ as $n$-dimensional submanifolds of $X$ (though this is not quite true) where we identify two submanifolds if we can deform one into the other inside of $X$.

For this reason, if $f$ and $g$ are the same up to deformation, then they should do the same thing to submanifolds up to deformation! ↩
Again, apologies to those new to the subject. More precisely, for each $n$ we have
\[f_n - g_n = \partial_{n+1}^B \circ H_n + H_{n-1} \circ \partial_n^A\]
notice, as promised in an earlier footnote, we’re using $\partial$ for the boundary maps on $A_\bullet$ and on $B_\bullet$. You really do get used to it. ↩
Astute readers will notice that a square is not a simplex, so we can’t really be reasoning about it using homology.

But anyone who’s made a grilled cheese knows we can divide a square into two triangles by cutting along a diagonal. Since $C_{2}(X)$ is comprised of formal sums of $2$-simplices (triangles) in $X$, we can identify this square with the sum of the two triangles inside it and nothing goes wrong.

The fact that we can always cut up $\Delta^n \times [0,1]$ into a bunch of $n+1$-simplicies is called the “prism argument”, and you can read about it on page $112$ of Hatcher. Again, to future proof this, this is in Section $2.1$.

It’s also worth noting that some people sidestep this issue by basing homology on “cubical chains” in $X$ rather than simplicial chains. Then we don’t need to go through the prism argument, since the $n$-cube times an interval is already an $n+1$-cube!

While this idea has gained a lot of traction in the HoTT community (since cubical foundations allow univalence to compute), it’s still somewhat nonstandard in the context of broader algebraic topology. See here for some discussion. ↩
You also shouldn’t have to wait too long if you really want to see me motivate model categories. Like I said at the start of the post, I’m super close to finishing a trilogy of blog posts, the first of which is about model categories!

If I remember (or when someone reminds me) I’ll link it here once the post is up. ↩
Obviously if we’re working with chains of $R$-modules rather than abelian groups, we should use $R$ here instead of $\mathbb{Z}$.

Also, I feel like there should be an “algorithmic” way of finding an interval object inside a model cateogry (again, really an $\infty$-category)… I know model categories can be pathological (for instance, depending on your definitions, certain constructions might not be functorial) but for most model categories that arise in pratice we don’t have these issues.

I want this to be a quick post, so I don’t want to look into it too much right now, but I would love to know if, say, every combinatorial model category has an interval object, and if we can reconstruct it (agian, maybe in the $\infty$-category setting) from the “walking interval”, namely the $\infty$-category with two objects joined by an equivalence.

If someone happens to know, I would love to hear about it ^_^ ↩
We can see that tensor products are the right notion of product (rather than the direct product) in a few ways:

First, the direct product would leave most of our chain complex unchanged. Contrast this with the tensor product, which successfuly gives us “off by one” pairs in each dimension that we expect (since we know we’re eventually going to recover the notion of chain homotopy)

Second, if you remember the Künneth Theorem, then you’ll remember that $H_n(X \times I)$ is related to $H_n(X) \otimes H_n(I)$.

Third, it seems like there’s a more general approach here that I don’t really understand. But again, I want this to be a quick post, so I won’t be doing that research myself (at least not tonight :P).

It looks like it has something to do with the tensor-hom adjunction, since $[0,1]$ is exponentiable, and we use both $X \times [0,1]$ and $X^{[0,1]}$ when studying the model structure on $\mathsf{Top}$.

Then we should be interested in some kind of monoidal closed type structure on the category of chains, where we use $A_\bullet \otimes I_\bullet$ and $[I_\bullet, A_\bullet]$ for the same purpose.

It seems like someone has made this precise (see remark 2.4 here, for instance), but I haven’t found any references myself. ↩
My instinct is to prove this, but I’m well over my planned one hour time limit on writing this post, and I have to wake up early tomorrow, so I should really get to bed.

So instead I’m taking the cop out as old as math itself, and I’m leaving this as an exercise.

I don’t feel too bad, though, since this is in the section that I said upfront would be a bit more technical, and the proof really isn’t hard (it’s a matter of unpcaking definitions more than anything else). Plus there’s a full proof on the nlab that I link to at the bottom of the exercise. ↩