What are Model Categories? (Homotopy Theories pt 1/4)

11 Jul 2022 - Tags: homotopy-theories

I’m a TA at the HoTTEST Summer 2022, a summer school about Homotopy Type Theory, and while I feel quite comfortable with the basics of HoTT, there’s a ton of things that I should really know better, so I’ve been doing a lot of reading to prepare. One thing that I didn’t know anything about was $\infty$ -categories, and the closely related model categories. I knew they had something to do with homotopy theory, but I didn’t really know how. Well, after lots of reading, I’ve finally figured it out, and I would love to share with you ^_^.

This was originally going to be one post, but it ended up having a lot of tangentially related stuff all mashed together, and it felt very disorganized and unfocused¹. So I’ve decided to split it into ~~three~~ four posts, with each post introducing a new, more abstract option, and hopefully saying how it solves problems present in the more concrete settings.

Let’s get to it!

First of all, what even is a “homotopy theory”? Let’s look at the primordial example:

Whatever a “Homotopy Theory” is, it should encompass the category $Top$ of topological spaces where we identify spaces up to (weak) homotopy equivalence

But there’s another motivating example, which we also call “homotopy”:

Whatever a “Homotopy Theory” is, it should encompass the chains of modules, where we identify two chains up to quasi-isomorphism

Obviously these are related – after all, from a topological space we can get an associated “singular cochain” of $R$ -modules. Then a homotopy of spaces induces a homotopy of cochains, and indeed the cohomology of the cochain complex agrees with the cohomology of the space we started with.

More abstractly, what links these situations? Well, we have some objects that we want to consider “the same up to homotopy”, and we capture this (as the category inclined are liable to do) by picking out some special arrows. These are the “homotopy equivalences” – and they’re maps that we want to think of as isomorphisms… but which might not actually be.

So, in $Top$ , we have the class of weak homotopy equivalences², which we want to turn into isomorphisms. And in $Ch (R -mod)$ , the category of chains of $R$ -modules, we want to turn the quasi-isomorphisms into isomorphisms.

With these examples in mind, what should a homotopy theory be?

A Relative Category is a small³ category $C$ equipped with a set of arrows $W$ (called the Weak Equivalences) that contains all the isomorphisms in $C$ ⁴.

Following our examples, we want to think of the arrows in $W$ as being morally isomorphisms, even though they might not actually be isomorphisms.

Now, a (small) category is an algebraic structure. It’s just a set with some operations defined on it, and axioms those operations satisfy. So there’s nothing stopping us from just… adding in new arrows, plus relations saying that they’re inverses for the arrows we wanted to be isomorphisms. By analogy with ring theory, we call this new category the Localization $C [W^{- 1}]$ . This is also called the Homotopy Category of $(C, W)$ .

For example, if we localize $Top$ at the weak homotopy equivalences, we get the classical homotopy category $hTop$ . If we invert the quasi-isomorphisms of chains of $R$ modules, we get the derived category⁵ of $R$ modules $D (R -mod)$ .

Tentatively, then, we’ll say that a homotopy theory is a category of the form $C [W^{- 1}]$ .

Notice that the choice of $(C, W)$ is far from unique. It’s entirely possible for two relative categories to have the same homotopy category⁶

C_{1} [{W_{1}}^{- 1}] ≃ C_{2} [{W_{2}}^{- 1}]

In this situation we say that $(C_{1}, W_{1})$ and $(C_{2}, W_{2})$ present the same homotopy theory.

There are many important examples of two relative categories presenting the same homotopy theory. To start, let’s consider the category $s Set$ of simplical sets, equipped with a notion of weak equivalence. It turns out that this presents the same homotopy theory as $Top$ with weak homotopy equivalences!

This means that if we have a question about topological spaces up to homotopy, we can study simplicial sets instead, with no loss of information! This is fantastic, since simplicial sets are purely combinatorial objects, so (in addition to other benefits) it’s much easier to tell a computer how to work with them⁷!

This is great, but there’s one hitch…

The homotopy category $C [W^{- 1}]$ might be terribly behaved. For instance, even if $C$ is (co)complete, the homotopy category almost never is⁸! Even worse, it’s possible that we end up with a proper class of arrows between two objects, even if $C$ started out locally small. Lastly, it’s difficult to tell when two relative categories present the same homotopy theory.

This is all basically because arrows in $C [W^{- 1}]$ are really hard to understand! After all, a general arrow from $A$ to $B$ in $C [W^{- 1}]$ looks like this:

A \tilde{\leftarrow} C_{0} \to C_{1} \tilde{\leftarrow} \dots C_{k} \to B

where all the $\tilde{\leftarrow}$ s are in $W$ . After we invert $W$ , these arrows all acquire right-facing inverses, which we can compose in this chain to get an honest arrow $A \to B$ .

There’s a zoo of techniques for working with homotopy categories, but they all come down to trying to tame this unwieldy definition of arrow⁹. In this post, we’ll be focusing on a very flexible approach by endowing $(C, W)$ with a Model Structure.

Roughly, to put a model structure on $(C, W)$ (which we now assume to be complete and cocomplete) is to choose two new subfamilies of arrows: the fibrations and the cofibrations.

From these, we define some “nice” classes of objects:

$X$ is called fibrant if the unique arrow to the terminal object is a fibration
$X$ is called cofibrant if the unique arrow from the initial object is a cofibration
$X$ is called bifibrant if it is both fibrant and cofibrant

Let’s see some examples:

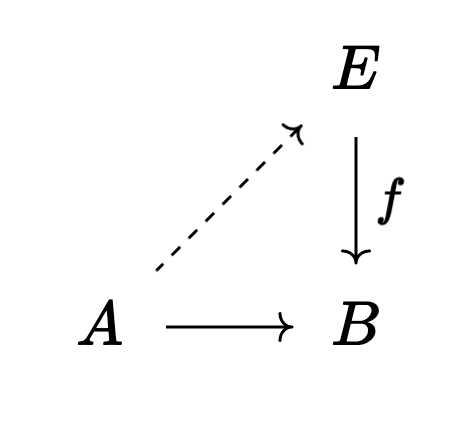
A fibration $f$ is an arrow that’s easy to “lift” into from cofibrant objects $A$ :

For instance, covering spaces and bundles are examples of fibrations in topology. If we restrict attention to the CW-complexes then every object is cofibrant, and this statement is basically the homotopy lifting property for covering spaces.

Algebraically, there’s a model structure where a map of chains of $R$ -modules $f : A_{∙} \to B_{∙}$ is a fibration if each $f_{n}$ is a surjection. The cofibrant objects in this model structure are exactly the levelwise projective complexes, so this lifting property becomes the usual lifting property for projective modules.

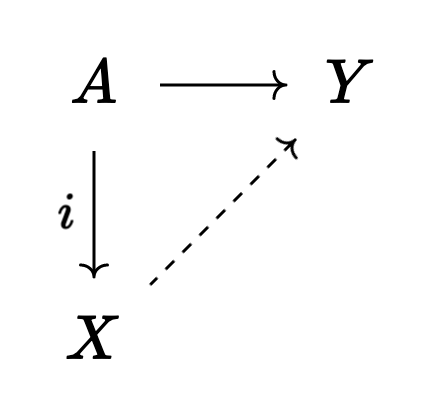
Dually, a cofibration $i$ is an arrow that’s easy to “extend” out of provided our target $Y$ is fibrant:

We should think of a cofibration as being a subspace inclusion $A ↪ X$ where $A$ “sits nicely” inside of $X$ .

For instance, the inclusion arrow of a “good pair” is a cofibration. Thus inclusion maps of subcomplexes of a simplicial/CW/etc. complex are cofibrations. More generally, any subspace inclusion $A ↪ X$ where $A$ is a nieghborhood deformation retract in $X$ will be a cofibration.

Algebraically, a map $f : A_{∙} \to B_{∙}$ is a cofibration exactly when each $f_{n}$ is an injection whose cokernel is projective¹⁰. This is a somewhat subtle condition, which basically says that each $B_{n} ≅ A_{n} \oplus P_{n}$ where $P_{n}$ is projective. It should be intuitive that given a map $A_{n} \to Y_{n}$ , it’s easy to extend this to a map $B_{n} \to Y_{n}$ under these hypotheses.

Precisely, these triangles are really special cases of squares. In the fibration case, the left side of the square is the unique map from the initial object to $A$ . Dually, in the cofibration case the right hand side of the square should really be the unique map from $Y$ to the terminal object.

This lets us unify these diagrams into a single axiom, which says that a square of the form

has a lift (the dotted map $X \to E$ ) whenever $i$ is a cofibration, $f$ is a fibration, and one of $i$ or $f$ is a weak equivalence.

The model category axioms¹¹ imply that every object is weakly equivalent to a bifibrant object. Since, after localizing, our weak equivalences become isomorphisms, this means we can restrict attention to the bifibrant objects… But why bother?

Well in any model category we have a notion of “homotopy” between maps $f, g : A \to B$ which is entirely analogous to the topological notion. Then by studying homotopy-classes of maps, we’ll be able to get a great handle on the arrows in $C [W^{- 1}]$ !

Precisely, each object $A$ is weakly equivalent to a cylinder object $A \times I$ which acts like $A \times [0, 1]$ in topology¹². In particular, it has two inclusions $ι_{0} : A \to A \times I$ and $ι_{1} : A \to A \times I$ .

⚠ This is not in general an actual product with some element $I$ . It’s purely notational. Some authors use $A \land I$ instead, but I don’t really like that either.

The best notation is probably $Cyl (A)$ or something similar, but in this post I want to emphasize the relationship with the classical topological case, so I’ll stick with $A \times I$ .

Now if $f, g : A \to B$ , then a homotopy between $f$ and $g$ is a map $H : A \times I \to B$ so that the following triangle commutes:

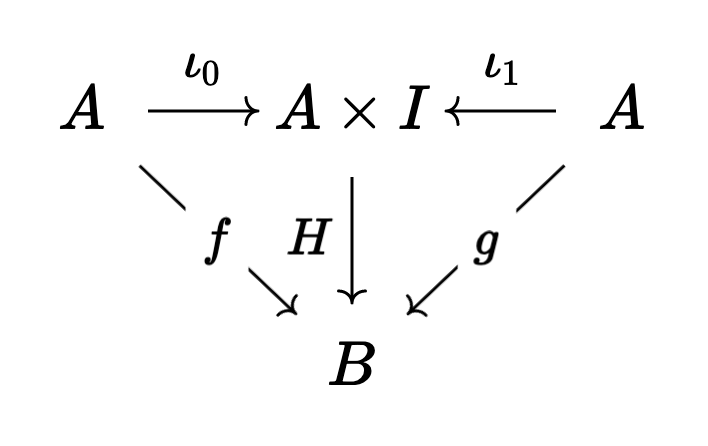
If there is a homotopy between $f$ and $g$ , we say that $f$ and $g$ are homotopic or homotopy equivalent, often written $f \sim g$ .

This brings us to the big punchline:

Let $(C, W)$ be a model category.

If $A$ and $B$ are bifibrant then homotopy equivalence really is an equivalence relation on ${Hom}_{C} (A, B)$ . Moreover, composition is well defined on the equivalence classes.
$C [W^{- 1}]$ is equivalent to the category whose objects are bifibrant objects of $C$ , and whose arrows are homotopy equivalence classes of arrows in $C$ .

Thus, a very common way we use model structures to perform computations is by first replacing the objects we want to compute with by weakly equivalent bifibrant ones. For instance, we might replace a module by a projective resolution¹³. Then maps in the homotopy category $C [W^{- 1}]$ are just maps in $C$ up to homotopy¹⁴!

Notice this, off the bat, solves one of the problems with homotopy categories. Maybe $C [W^{- 1}]$ isn’t locally small, but it’s equivalent to something locally small.

Moreover, model structures give us a very flexible way to tell when two relative categories have the same homotopy theory. Indeed, say we we have a pair of adjoint functors $L ⊣ R$ between $C_{1}$ and $C_{2}$ that respect the weak equivalences in the sense that $f : c_{1} \to R (c_{2})$ is in $W_{1}$ if and only if its adjoint $\tilde{f} : L (c_{1}) \to c_{2}$ is in $W_{2}$ . Then $C_{1} [W_{1}^{- 1}] ≃ C_{2} [W_{2}^{- 1}]$ , and moreover, this equivalence can be computed from the adjunction $L ⊣ R$ .

This is called a Quillen Equivalence between $(C_{1}, W_{1})$ and $(C_{2}, W_{2})$ ¹⁵.

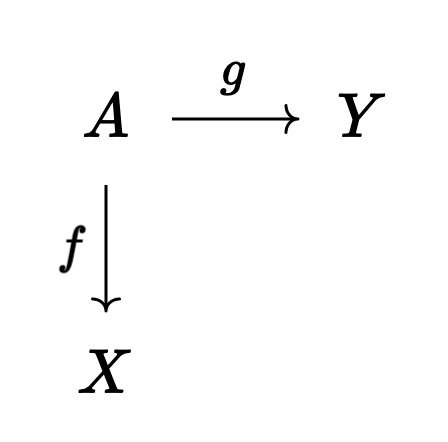
Moreover again, even if $C [W^{- 1}]$ doesn’t have (co)limits, we can always construct homotopy (co)limits, which we can compute using the same cylinder objects from before. For instance, the homotopy pushout of

will be the colimit of the related diagram:

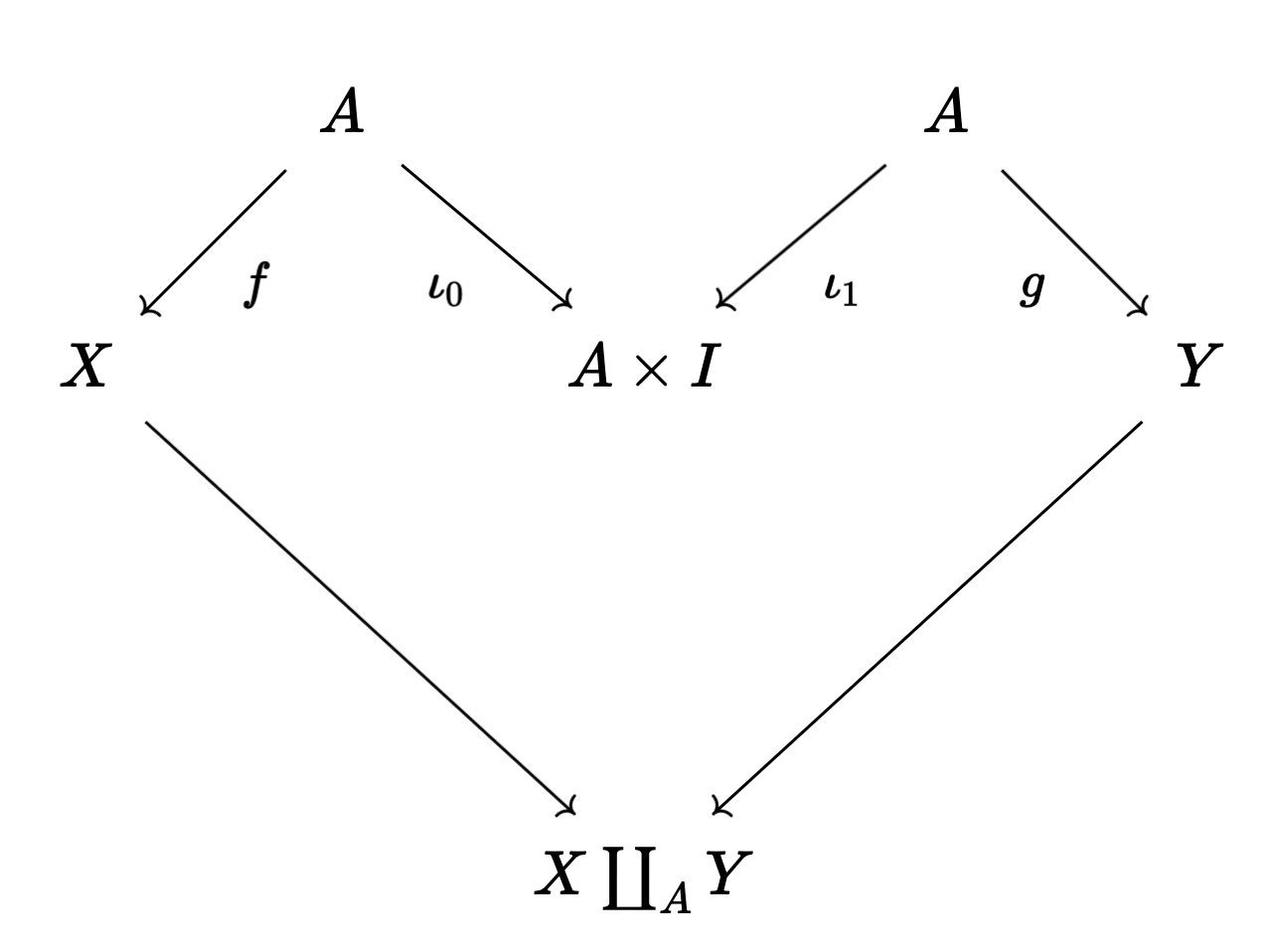
Geometrically, rather than gluing $X$ to $Y$ along $A$ directly, we’re adding a path from $f (a)$ to $g (a)$ . This is the same up to homotopy, but is better behaved. We do this by taking disjoint copies of $X$ and $Y$ , and then gluing one side of the cylinder $A \times I$ to $X$ along $f$ , and gluing the other side of $A \times I$ to $Y$ along $g$ .

Something like this will always work, but knowing how to modify our diagram (and why) can be quite involved¹⁶. Thus we’ve succeeded in computationally solving the (co)limit issue, but it would be nice to have a more conceptual framework, in which it’s obvious why this is the “right thing to do”…

We’ve seen that a model structure on a relative category helps to make computations in the localized category $C [W^{- 1}]$ effective (or even possible). But model categories have a fair number of problems themselves.

For one, there’s no great notion of a functor between model categories. In the case that a functor $F : (C_{1}, W_{1}) \to (C_{2}, W_{2})$ comes from and adjoint pair, then we can derive it to get a functor on the homotopy categories, but this is too restrictive to be the general notion of functor between model categories.

Related to functors, if $C$ has a model structure and $I$ is an indexing category, then $C^{I}$ , the category of $I$ -diagrams in $C$ (with the pointwise weak equivalences) may not have a model structure. See here, for instance¹⁷.

With this in mind, we would like to have a version of the theory of model categories which has better “formal properties”. While working with a single model category is often quite easy to do, as soon as one looks for relationships between model categories, we’re frequently out of luck. In fact, since (co)limits come from functors, as soon as we’re interested in (co)limits we already run into this problem! This is one philosophical reason for the complexity of homotopy (co)limits.

The solution lies upwards, in the land of $\infty$ -categories. These are categories with homotopy theoretic structure (in the classical sense of topological spaces) built in from the start. Miraculously, these will solve all the above problems and more – while the category of model categories is a terrible place to live (if we can define it at all…) the category of $\infty$ -categories¹⁸ is extremely similar to the category of categories. Then, since every model category presents an $\infty$ -category, we’ll be able to use this machinery to solve our formal problems with model categories!

How exactly does this work? You’ll have to read more in part 2!

This is one of the biggest problems with trying to explain things you know. Especially while you’re still trying to sort them out yourself!

All of this material was scattered in my head with messy interconnections, but of course words have to be linearly ordered on a page, and it took a lot of work to figure out how to put these ideas into a fixed order. Especially one which has a nice narrative.

It’s currently my fifth time restarting this post (now ~~trilogy~~ tetralogy), but I think I’m finally happy with my outline. I don’t know why I’m writing this footnote, to be honest. But it felt like something I wanted to say, so here we are.

On with the show! ↩
It turns out there’s also a model category structure whose homotopy category gives homotopy equivalence, rather than weak homotopy equivalence.

But the model structure on $Top$ which gives weak homotopy equivalence is the “standard” one, so that’s what I’m listing as the motivating example. ↩
A better word would probably be “strict”. Since we’re going to be treating $C$ like an algebraic structure pretty soon, it should have fixed sets of objects and arrows, which we will manipulate like we might manipulate the underlying set of a group, ring, etc. ↩
Be careful, though, I’ve seen a handful of other definitions too!

I like this one because it means the obvious way to turn a category into a relative category is to take just the isomorphisms. Then localization from $RelCat \to Cat$ is left adjoint to the functor sending $C$ to $(C, isos)$ .

I’m not sure if I should require that $W$ be closed under composition… This doesn’t feel like it should break anything, but I’m not 100% sure. ↩
This was a pleasant surprise for me. I’ve heard a lot of talk about derived categories, and they always seemed quite scary. It’s been very exciting to feel like I’m getting a two-for-one deal every time I notice another concept in this subject start to make sense – after all, it means I’m learning about both homotopy theories and derived categories! ^_^ ↩
As an aside, as a topos theorist, this all feels a bit familiar.

Just like a model structure (which we’ll define later) is some structure that presents a homotopy theory in a way that lets us do concrete computation, a site is a structure that presents a (grothendieck) topos and lets us do concrete computations.

Now, in the topos theory world, Olivia Caramello’s bridges program is based on the idea that we can find nontrivial relationships between two sites presenting the same topos… I wonder if there are any theorems that let us relate two model categories presenting the same homotopy theory. ↩
See, for instance, the sage documentation here and here. ↩
Even in the case of $hTop$ , we don’t have all (co)limits! See here, for instance! ↩
For instance you can only look at families $W$ satisfying the Ore Conditions. These say exactly that we can “commute” weak equivalences past other arrows. Then, up to homotopy, every arrow in the localization is of the form
$A \tilde{\leftarrow} C \to B$
and these are quite easy to manipulate.

See Sasha Polishchuk’s lectures on Derived Categories here, for a really nice treatment using this language. ↩
Really we’re describing the projective model structure here. There’s a dual model structure with the same weak equivalences where we work with injectives instead. ↩
Which I still haven’t really told you, haha.

I don’t want to get into the precise details of a model structure here, but you can (and should!) read more in Dwyer and Spalinski’s excellent introduction Homotopy Theory and Model Categories, available here, for instance.

There’s a lot of good places to get intuition for model structures as well.

For instance, Mazel-Gee’s The Zen of $\infty$ -Categories, avaialable here, Kantor’s survey Model Categories: Theory and Applications, available here, and of course, the nlab.

While we’re at it, there’s also Goerss and Schemmerhorn’s Model Categories and Simplicial Methods (here), Hovey’s book (here), and you can find a lot of good intuition in the MO questions here, here, here, and here. There’s also Ponto and May’s More Concise Algebraic Topology (here)… I could keep going, but I should probably get back to writing the main body of the post. ↩
We build $A \times I$ by factoring the codiagonal $A ∐ A \to A$ as
$A ∐ A \to A \times I \tilde{\to} A$
where $A ∐ A \to A \times I$ is a cofibration and where $A \times I \tilde{\to} A$ is both a fibration and a weak equivalence. ↩
This is made even more useful by the existence of multiple model structures on $(C, W)$ . Depending on the computation, we might choose one model structure over another in order to make our lives as simple as possible. For instance, we have two model structures on chain complexes, one based on projectives and one based on injectives. Then computations involving these model structures reduce to the classical projective or injective resolutions which you may recognize from homological algebra! ↩
For an example of this idea in action, see this answer of mine. ↩
For example, the earlier example of $Top$ and $s Set$ , which have the same homotopy theory, comes from a quillen equivalence. See here, for instance.

In fact, quillen equivalence is stronger tronger way than we currently have the language to describe. Not only are the localizations (read: homotopy categories) equivalent, but actually the presented $\infty$ -categories are equivalent too! ↩
Even though it’s complicated, this is a solved problem. We understand how to take a diagram and massage it into a new, “homotopy coherent” diagram. The idea is again one of bifibrant replacement!

In many cases we can put a model structure on the category of functors into a model category $C$ . Then instead of taking the (co)limit of a diagram $F$ , we cake the (co)limit of its bifrant replacement.

See either the notes by Dugger here or by Hirschhorn here for specifics.

Also, after reading those, notice that already the best way to organize this data is with some kind of simplicial object… and keep a pin in that. ↩
Though, thankfully, most model categories that arise in practice are (quillen equivalent to) a (simplicial) combinatorial model category.

In particular, this means that we can usually put a model structure on the category of diagram in $C$ . In fact, this is one way to effectively compute homotopy (co)limits in practice. We replace our functor $F : I \to C$ by a weakly equivalent bifibrant functor $\tilde{F} : I \to C$ and then output the (weak equivalence class of) the (co)limit of $\tilde{F}$ .

This is basically the derived functor approach to homotopy (co)limits, and while it’s effective, it requires us to choose a bifibrant replacement. Much like choosing coordinates or a basis makes some proofs more annoying in the setting of differential geometry or linear algebra (since we then have to prove our results are independent of this choice), we would like to have a choice-free way of defining homotopy (co)limits. ↩
In fact, it eats its own tail, and we have an $\infty$ -category of $\infty$ -categories. But more on that later. ↩