Why Care About Infinity Categories? (Homotopy Theories pt 2/4)
11 Jul 2022 - Tags: homotopy-theories
The title of this post is slightly misleading. It will be almost entirely about $\infty$-categories, but it will have a focus on how $\infty$-categories solve some of the formal problems with model categories that we outlined in part 1 of this trilogy.
With the intro out of the way, let’s have a quick recap.
The setting we’re interested in is a category $\mathcal{C}$ equipped with some arrows $\mathcal{W}$ that morally should be isomorphisms, but which aren’t (these are called weak equivalences, and a pair $(\mathcal{C}, \mathcal{W})$ is called a relative category). The quintessential examples are the (weak) homotopy equivalences in $\mathsf{Top}$, and the quasi-isomorphisms of chain complexes.
We want to build a new category (called the homotopy category or localization) $\mathcal{C}[\mathcal{W}^{-1}]$ where we freely invert all the arrows in $\mathcal{W}$1. The issue is that this category is quite badly behaved. For instance, even if $\mathcal{C}$ is (co)complete, $\mathcal{C}[\mathcal{W}^{-1}]$ almost never is.
A model structure on a pair $(\mathcal{C}, \mathcal{W})$ is a choice of two new families of arrows, called fibrations and cofibrations, plus axioms saying how they relate to each other and to the weak equivalences $\mathcal{W}$.
A model structure on $(\mathcal{C}, \mathcal{W})$ solves many of the computational problems with $\mathcal{C}[\mathcal{W}^{-1}]$. For instance, now the homotopy category is guaranteed to be locally small, and we have effective techniques for computing homotopy (co)limits, derived functors, and guaranteeing that two relative categories have equivalent localizations. All of these techniques go through bifibrant replacement, which is a generalization of the familiar projective and injective resolutions from homological algebra.
Unfortunately, as we noted at the end of the last post, model categories are not without flaws. As soon as we want to talk about relationships between model categories, we start running into trouble. For instance, there’s no good notion of a functor between model categories.
What, then, are we to do? The answer is to fully accept homotopy theory as part of our life, and to move to a notion of “category” which is better equipped to handle the geometry which is implicit in the machinery of model categories.
To start, we need a model of “spaces” that’s more convenient to work with than topological spaces.
A Simplicial Set is a functor $X : \Delta^{\text{op}} \to \mathsf{Set}$.
Here $\Delta$ (the simplex category) is the category whose objects are the nonemtpy finite totally ordered sets, with order preserving maps.
Every object in $\Delta$ is isomorphic to an object of the form
\[0 \lt 1 \lt 2 \lt \ldots \lt n\]which we call $\Delta^n$.
We should think of $\Delta^n$ as representing the $n$-simplex, where we’ve chosen a total order the $n+1$ vertices. This allows us to orient all the edges in a consistent way2.
Now, to every topological space $X$ we can associate a simplicial set $\text{Sing}_X$, where $\text{Sing}_X(\Delta^n)$ is the set of continuous from the (topological) $n$-simplex into $X$. This construction is familiar from, for instance, singular homology.
It turns out that \(\text{Sing}_X\) perfectly remembers the homotopy type of $X$, in the sense that we can recover $X$ (up to homotopy equivalence) knowing only the simplicial set \(\text{Sing}_X\). This is some justification that simplicial sets really can be used to model homotopy types.
But there’s a natural follow up question: Can we recognize when a simplicial set is \(\text{Sing}_X\) for some space $X$? The answer, of course, is yes, but we’re not going to talk about that here. This topic deserves its own post, which is part 3.
For now we’ll content ourselves with the knowledge that simplicial sets, up to homotopy equivalence, represent spaces in a convenient way. For those following along, this is the Quillen equivalence between $s\mathsf{Set}$ and $\mathsf{Top}$ that we mentioned in the previous post!
We’ll write $\mathcal{S}$ for the homotopy category of $s\mathsf{Set}$ (equivalently of $\mathsf{Top}$), and we’ll call the objects of this category spaces.
A Simplicial Category is a category enriched in $\mathcal{S}$.
That is, given two objects $A$ and $B$ in our category, we have a space of morphisms $\text{Map}(A,B)$.
There is a natural notion of equivalence between two simplicial categories, called Dwyer-Kan equivalence, then we (tentatively) say an $\infty$-category is a simplicial category up to DK-equivalence.
Given an $\infty$-category $\mathcal{C}$, there’s a natural way to get an ordinary category back from it. We keep the same objects, but replace the space of arrows $\text{Map}(A,B)$ by its set of connected components. We call this the Homotopy Category of $\mathcal{C}$.
As an example, we might have two arrows $f,g : A \to B$, which are connected by homotopies $H$ and $K$. In this case we have a “circle’s worth” of arrows from $A \to B$:
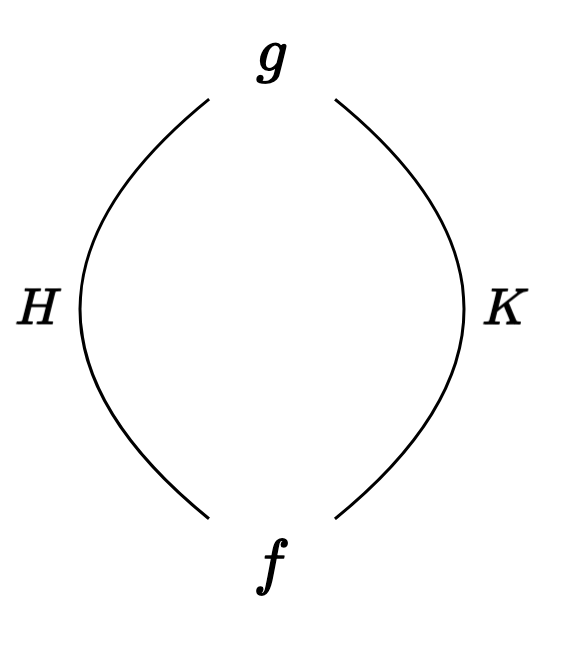
When we take connected components, these two maps $f$ and $g$ are identified, so we only see one arrow in the homotopy category.
We’ll see another, more realistic example, once we know how to build an $\infty$-category from a relative category $(\mathcal{C}, \mathcal{W})$.
So how do we build an $\infty$-category from a relative category? This is called the Hammock Construction3, and while we won’t spend too much time on this, it’s worth at least a few words!
We want to build up a space of maps $A \to B$.
The $0$-cells will be zigzags of the form:
- \[A \to B\]
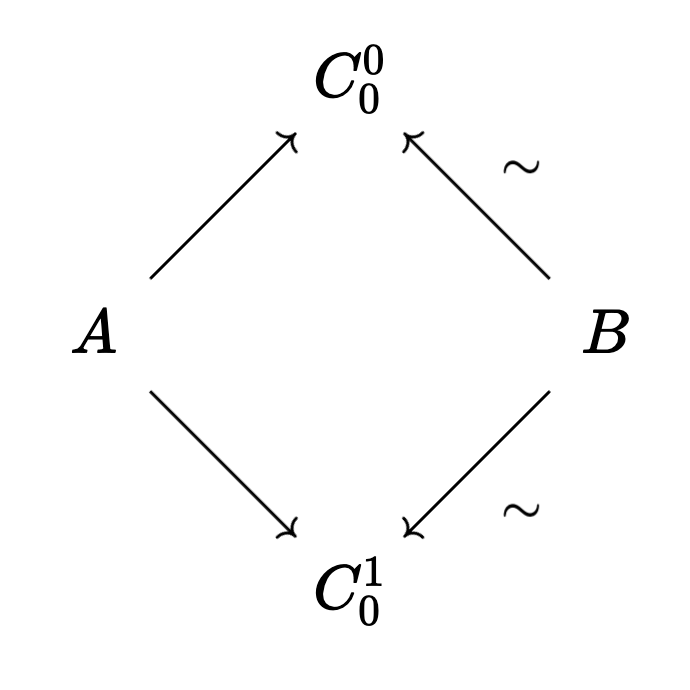
- \[A \to C_0 \overset{\sim}{\leftarrow} B\]
- \[A \to C_0 \overset{\sim}{\leftarrow} C_1 \to B\]
- \[A \to C_0 \overset{\sim}{\leftarrow} C_1 \to C_2 \overset{\sim}{\leftarrow} B\]
- etc.4
where the left-pointing arrows are weak equivalences. Notice that, after we invert the weak equivalences, the left facing arrows will have inverses, which will compose with the other right facing arrows to give an honest-to-goodness arrow $A \to B$. That is, the $0$-cells really are maps $A \to B$ in $\mathcal{C}[\mathcal{W}^{-1}]$.
Now, a $1$-cell from $f$ to $g$ should be a “proof” that $f$ and $g$ are homotopic. If $f$ and $g$ have the same length, then we can represent this with a “hammock”5:
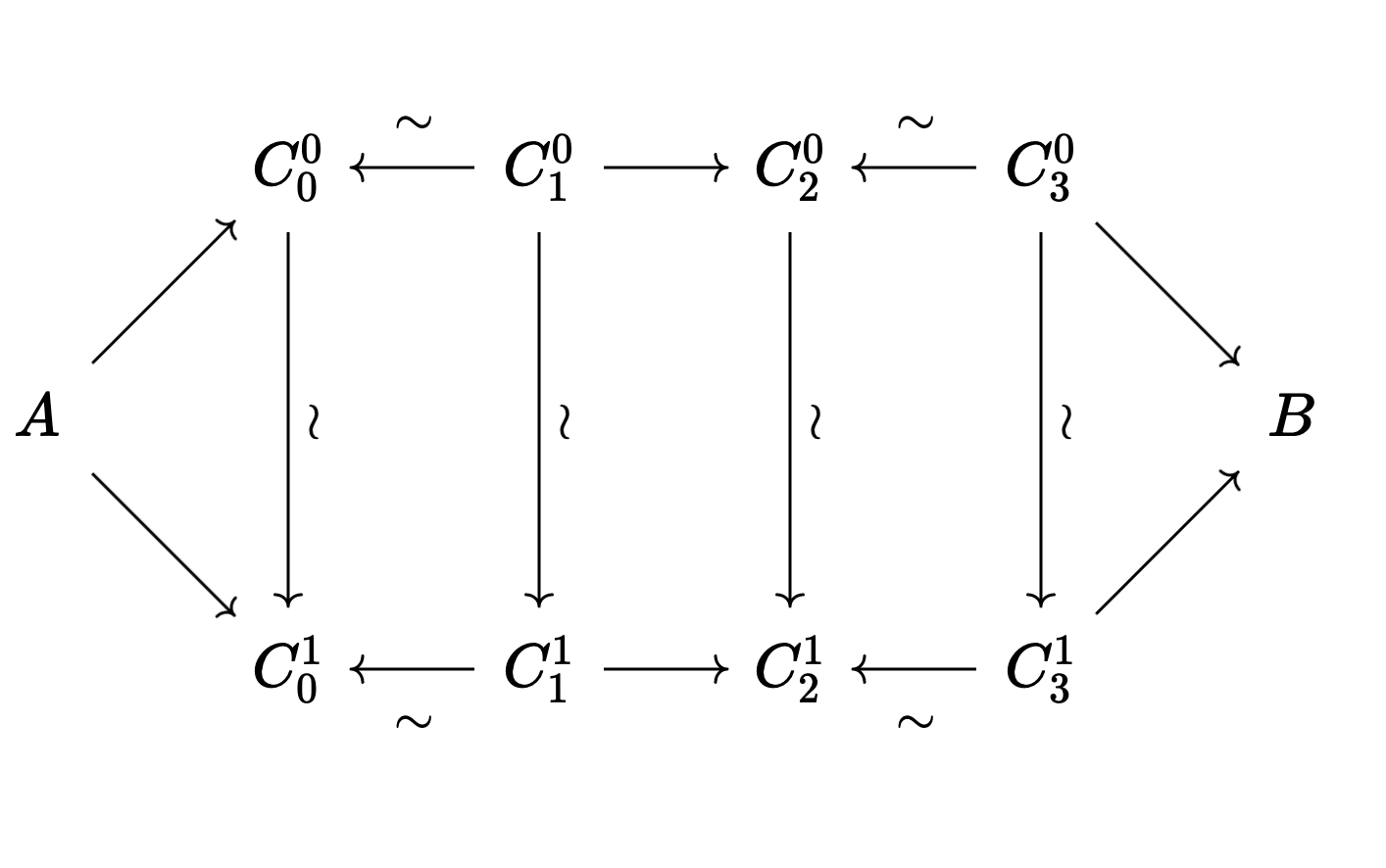
Similarly, a $k$-cell will be a hammock that is $k$ strands “wide”. Here’s the picture from the original paper:
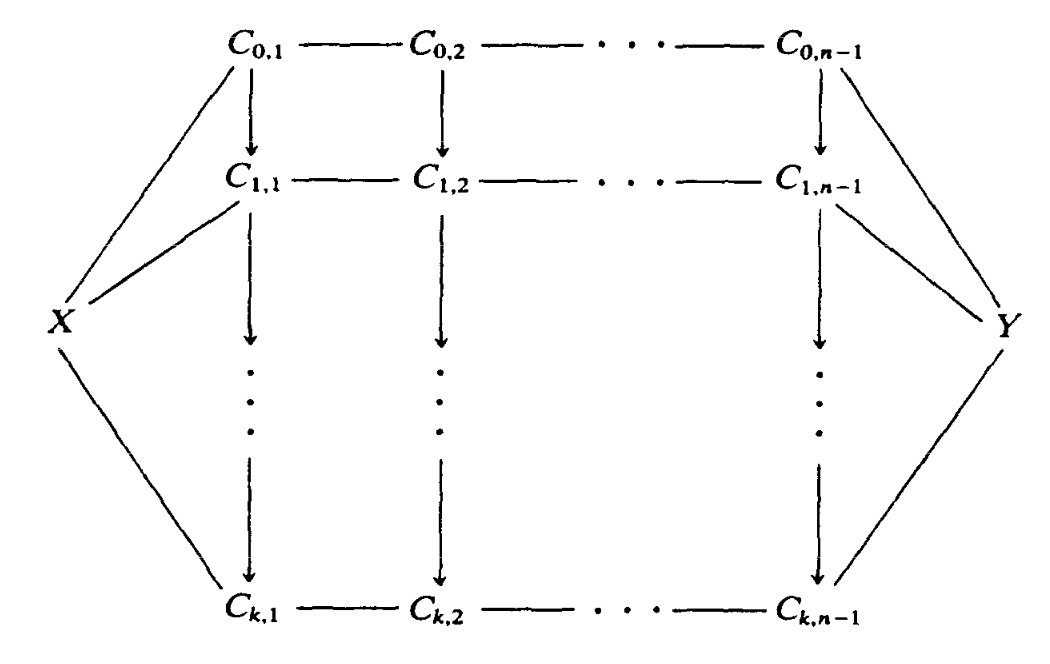
As before, the vertical arrows should all be weak equivalences, as should all the backwards facing arrows in the zigzags.
Of course, we need the face maps between simplicies. We get the $i$th face map by just omitting row $i$ from the hammock. We get the $i$th degeneracy map by repeating the $i$th row, using the identity map in each column as the weak equivalence.
The resulting $\infty$-category $L^H(\mathcal{C}, \mathcal{W})$ is called the (Hammock) Simplicial Localization of $(\mathcal{C}, \mathcal{W})$.
Notice that the homotopy category of $L^H(\mathcal{C}, \mathcal{W})$ is equivalent to the category $\mathcal{C}[\mathcal{W}^{-1}]$, so we can recover the “classical” localization from the hammock localization whenever we want.

Let’s see an example. Consider the category
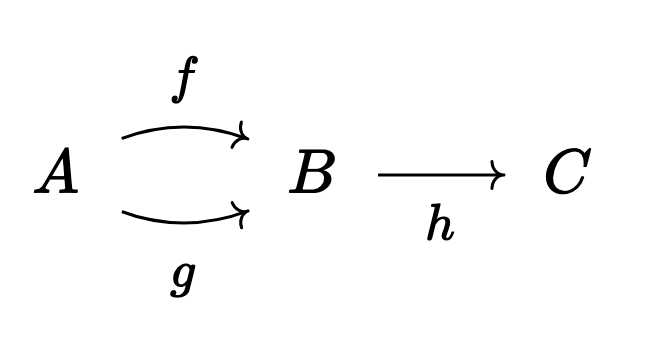
where $hf = hg = k$.
Say we want to invert $h$. After doing this we see that $f = g$, since we must have $f = h^{-1} k = g$. Thus we have lost information in the homotopy category that we didn’t necessarily plan on losing when we inverted $h$. Does the hammock localization solve this problem?
Let’s compute $\text{Map}(A,B)$.
It should have a $0$ cell for each zigzag. So we’ll have $0$-cells
- $A \overset{f}{\to} B$
- $A \overset{g}{\to} B$
- $A \overset{k}{\to} C \overset{h}{\underset{\sim}{\leftarrow}} B$
For $1$-cells, we’ll have two small hammocks:
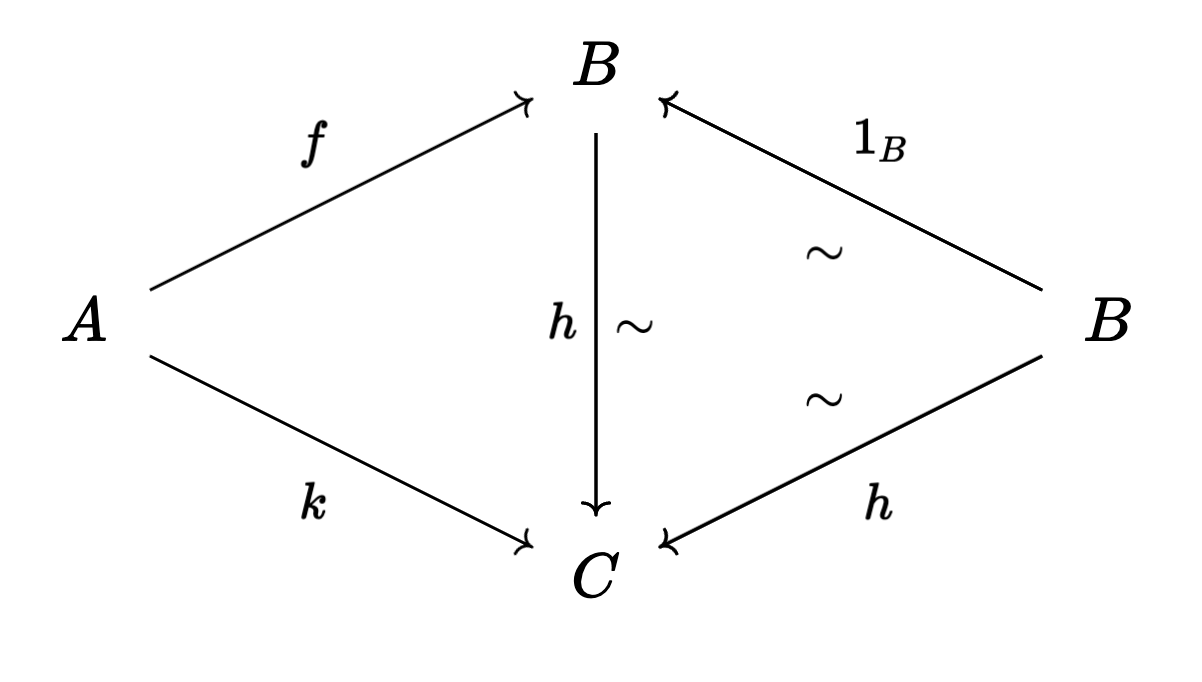
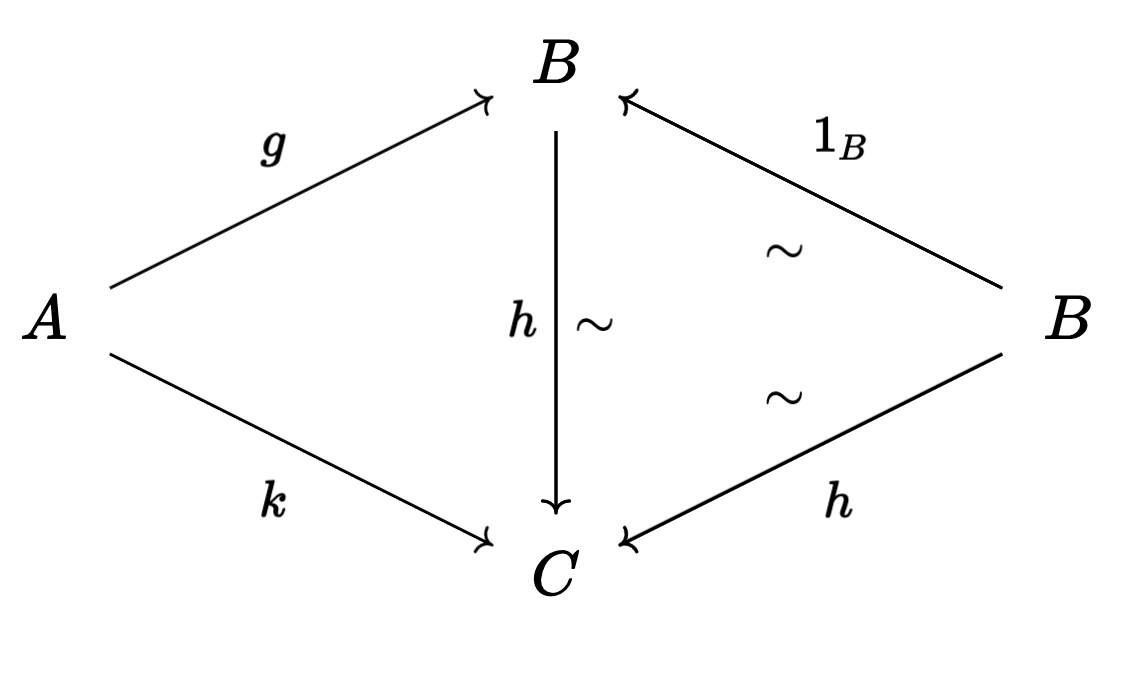
So that $\text{Map}(A,B)$ is the space:

which is, of course, contractible. Crucially, though, this space is capable of remembering more information about how the maps $A \to B$ in $\mathcal{C}[\mathcal{W}^{-1}]$ were built from maps in $\mathcal{C}$, and how these relate to each other.
Consider instead the category
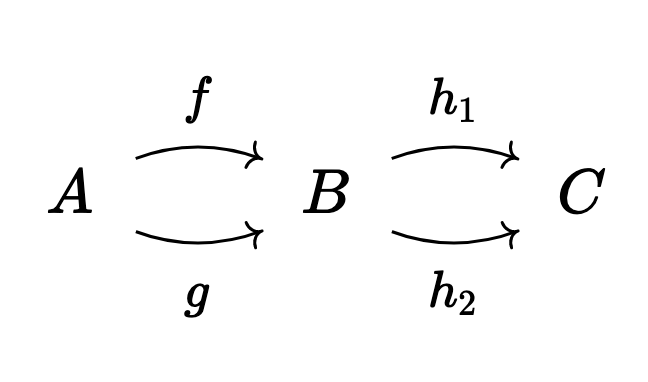
where $h_1 f = h_1 g = k = h_2 f = h_2 g$.
Show that, after inverting $h_1$ and $h_2$, $\text{Map}(A,B)$ is a circle.
This is great, but it’s far from clear how we would do this for more complicated categories! This is ok, though. Remember that $\infty$-categories are conceptually nice but if you have a specific category in mind, model categories are where we actually want to do our computations.
It begs the question, though: just how nice are $\infty$-categories? After all, this abstraction needs to justify itself somehow.
Let’s start with the most obvious issue with model categories: the lack of functors between them. Once we pass to $\infty$-categories, then we know exactly what to do! We have a good theory of functors between enriched categories, and you can probably guess what the correct idea should be:
If $\mathcal{C}$ and $\mathcal{D}$ are simplicial categories, then a Simplicial Functor $F : \mathcal{C} \to \mathcal{D}$ is a pair
- $F_\text{obj}$ sending each object of $\mathcal{C}$ to an object of $\mathcal{D}$
- $F_\text{map}$ which is a map of simplicial sets from each \(\text{Map}_\mathcal{C}(A,B) \to \text{Map}_\mathcal{D}(F_\text{obj}A, F_\text{obj}B)\)
Importantly, we have exactly one notion of functor between model categories, namely the quillen equivalences. We would like to know that these are faithfully preserved when we pass to $\infty$-categories, and indeed they are. One can show that every quillen equivalence of model categories gives rise to an equivalence (in the sense of $\infty$-categories) between the two $\infty$-categories they present.
Next, not only do we have a notion of functor, but we have a notion of functor which acts the way we expect it to. For instance between any $\infty$-categories $\mathcal{I}$ and $\mathcal{C}$, the collection of $\infty$-functors between them assembles into an $\infty$-category $\text{Fun}(\mathcal{I}, \mathcal{C})$ with a simplicial analogue of natural transformations as the arrows6.
From here, developing (co)limits is easy!
If $F : \mathcal{I} \to \mathcal{C}$ is a functor, then a Cone over $F$ is an object $c \in \mathcal{C}$ plus a (simplicially enriched) natural transformation from the constant $c$ functor $\text{const}_c$ to $F$.
We say that a cone on $c$ is a Limit Cone if for every object $x \in \mathcal{C}$, the natural map
\[\text{Map}_\mathcal{C}(x,c) \to \text{Map}_{\text{Fun}(\mathcal{I},\mathcal{C})}(\text{const}_x, F)\]is an equivalence of simplicial sets7.
If this looks like an adjunction between a “limit” functor and the “const” functor, then you’d be right! We can actually develop adjunctions in this theory as well, and indeed basically any construction or theorem you would want to use from classical $1$-category theory exists in some form in $\infty$-category theory!
So, miraculously, in the passage from model categories to $\infty$-categories, not only have we solved our quibbles about the formal properties of model categories, but we’ve done so in the most powerful possible way! We have access, in the $\infty$-category setting, to all the nice formal properties that made classical $1$-category theory so effective.
What’s even more remarkable is that this notion of a (co)limit computes homotopy (co)limits as a special case!
In the next post about quasicategories, we introduce the nerve construction, which lets us build an $\infty$-category from a $1$-category. Well if $\mathcal{C}$ is a model category, then a homotopy (co)limit of some functor $F : \mathcal{I} \to \mathcal{C}$ is the same thing as the $\infty$-category theoretic colimit of the induced ($\infty$-)functor $\tilde{F}$ from the nerve of $\mathcal{I}$ to $L^H(\mathcal{C}, \mathcal{W})$.
Lastly, let’s note that this is all good for something. Functors on $\infty$-categories can be “truncated” in a way that induces functors on the homotopy categories (see here, for instance). This means that, at least in the abstract, we can prove theorems using the language of $\infty$-categories, and at the end of the day we can take homotopy categories. After doing this any categories or functors we’ve built will descend nicely. In particular, since the homotopy category of $L^H(\mathcal{C}, \mathcal{W})$ is $\mathcal{C}[\mathcal{W}^{-1}]$ this gives us a very powerful mode of argument for dealing with localizations!
This still leaves open some questions, though. First, it seems like there are two competing notions of $\infty$-category. We can use simplicial categories or we can use quasicategories. Since we want to think about relative categories and $\infty$-categories as both presenting homotopy theories, we now have three different ways we could define “homotopy theory”!
Moreover, while the hammock localization is nice, it seems really annoying to work with. Can we play the game one more time, and end up with a conceptually clean way to see what the hammock localization is “really doing”?
For answers to both of these questions, I’ll see you in the
last post of this trilogy… tetralogy?
Maybe it’s best to call it a trilogy with a long quasi-categorical ~bonus post~.
Take care, all ^_^
-
Think about $\mathsf{Top}$ where we invert all the (weak) homotopy equivalences, or chain complexes of modules where we invert all the quasi-isomorphisms. ↩
-
Notice this is exactly what we do to make (co)homological computations with simplicial chains in topology. ↩
-
You can read more in the (surprisingly readable!) paper Calculating Simplicial Localizations by Dwyer and Kan.
Another approach to simplicial localization is explained in another readable paper by the same authors: Simplicial Localizations of Categories. It’s a perfectly good definition, and works well in the abstract, but the “hammock” definition is more amenable to direct computation, since it’s slightly more explicit.
-
It’s actually slightly more general. The first arrow is also allowed to point left, as long as things still alternate. For instance, we allow a zigzag of the form
\[A \overset{\sim}{\leftarrow} C_0 \to B\]as well.
For the specifics of the construction, see Calculating Simplicial Localizations by Dwyer and Kan. ↩
-
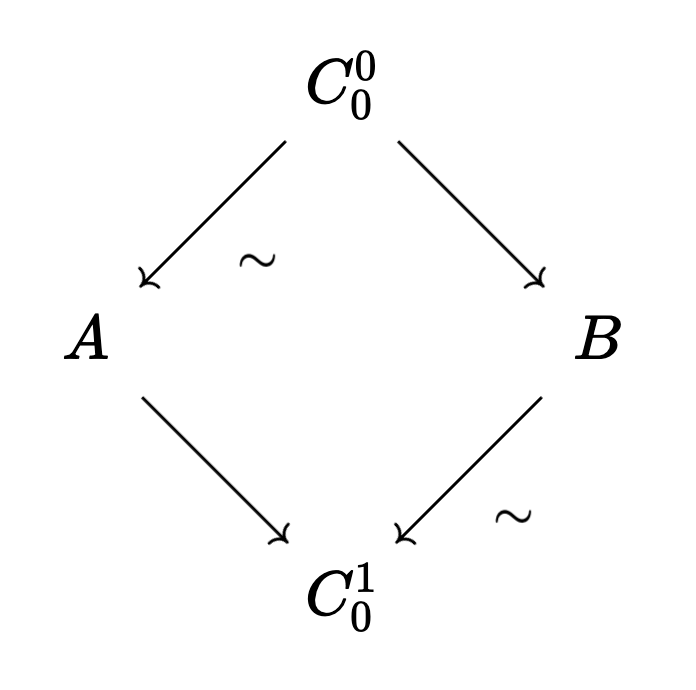
As before, we also allow the first map to face left instead of right, as long as our maps strictly alternate. What does this mean for our hammocks? The horizontal threads of our hammock must be oriented the same way!
For instance, this is a valid hammock:
This is a valid hammock:
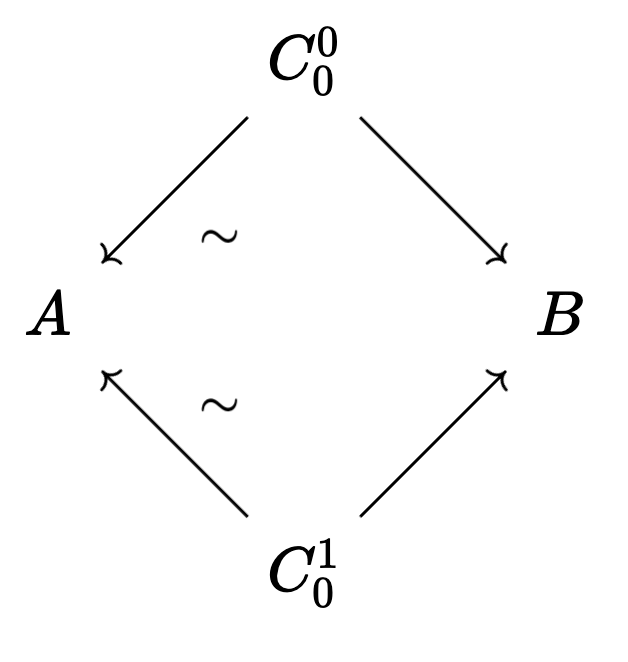
But this is not a valid hammock:
Also, I can’t express enough how much I love this naming idea! It’s quirky and apt in equal measure. 10/10. ↩
-
We can actually get by with slightly less. $\mathcal{I}$ is allowed to be any simplicial set. To see why this is more general, I’ll again point you to the quasicategory post here. ↩
-
If you want to learn about actually computing with $\infty$-categories, I can’t recommend the Homotopy Theory Münster videos here highly enough!
The second video already shows lots of sample computations for limits. ↩