An Interlude -- Quasicategories (Homotopy Theories pt 3/4)

11 Jul 2022 - Tags: homotopy-theories

In the previous post, we defined $\infty$ -categories as being categories “enriched in simplicial sets”. These are nice, and fairly quick to introduce, but if you start reading the $\infty$ -category theoretic literature, you’ll quickly run into another definition: Quasicategories. In this post, we’ll give a quick introduction to quasicategories, and talk about how they’re related to the $S$ -enriched categories we’ve come to know and love.

First, then, a reminder:

A Simplicial Set is a (contravariant) functor from the simplex category to $Set$ .

This seems strange at first, but it turns out that we can model many different kinds of behavior using simplicial sets.

Most notably, simplicial sets are a common generalization of both topological spaces (up to homotopy) and categories!

We’ve already seen how simplicial sets can represent topological spaces up to homotopy (this is given by a quillen equivalence of model structures on $Top$ and $s Set$ ). To a simplicial set, we associate its geometric realization, and to a topological space we associate its (singular) simplicial set ${Sing}_{X}$ where ${Sing}_{X} (Δ^{n})$ is the set of continuous maps from the topological $n$ -simplex into $X$ .

We know that $X$ is determined up to (weak) homotopy equivalence by ${Sing}_{X}$ , so we previously defined a Simplicial Category to be a category enriched in simplicial sets. We wanted to intuitively view this as a category with a geometric space of arrows between any two objects, as this came up in our study of $\infty$ -categories. This turns out to be a great definition for intuition, but it can be a bit difficult to work with.

I mentioned earlier that simplicial sets can directly generalize categories… Maybe there’s some way to define $\infty$ -categories directly as simplicial sets as well?

The answer will be “yes”, but let’s start small. Is there a way for us to recognize when a simplicial set is ${Sing}_{X}$ for some topological space $X$ ?

The $i$ th Horn of $Δ^{n}$ is (geometrically) the space we get by removing the interior of $Δ^{n}$ , along with the face opposite the $i$ th vertex¹. We denote it $Λ_{i}^{n}$

For instance, let’s look at $Δ^{2}$ . This is a solid triangle, and it has three horns – one for each vertex.

Concretely, $Δ^{2}$ is given by

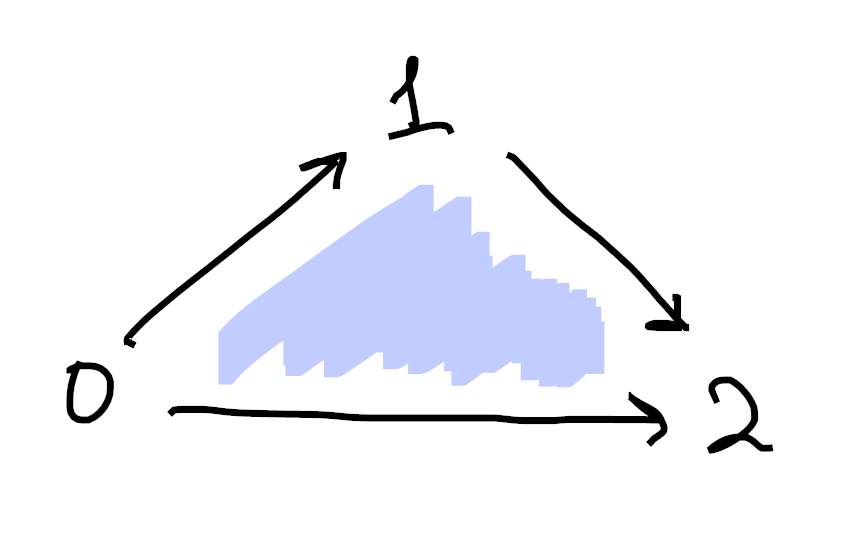
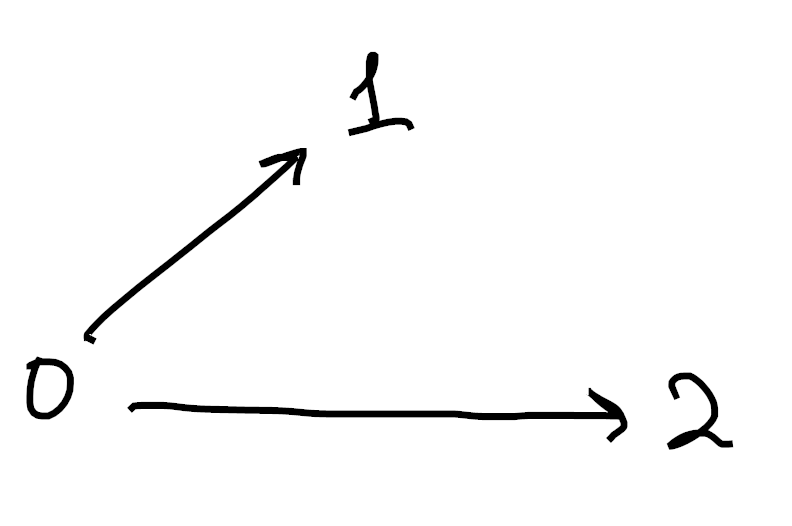
Then the $0$ th horn of $Δ^{2}$ , denoted $Λ_{0}^{2}$ , is what we get by removing the interior 2-cell, along with the 1-cell opposite $0$ :

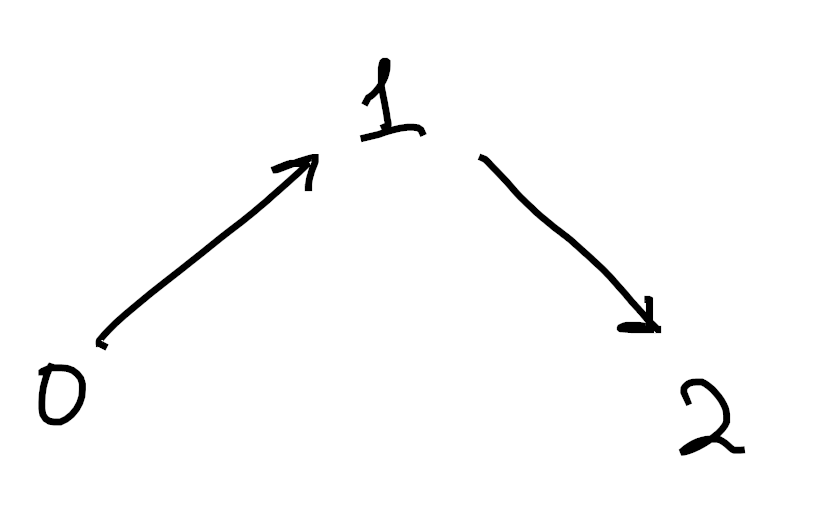
Analogously, we get $Λ_{1}^{2}$ by removing the interior 2-cell and the 1-cell opposite $1$ :

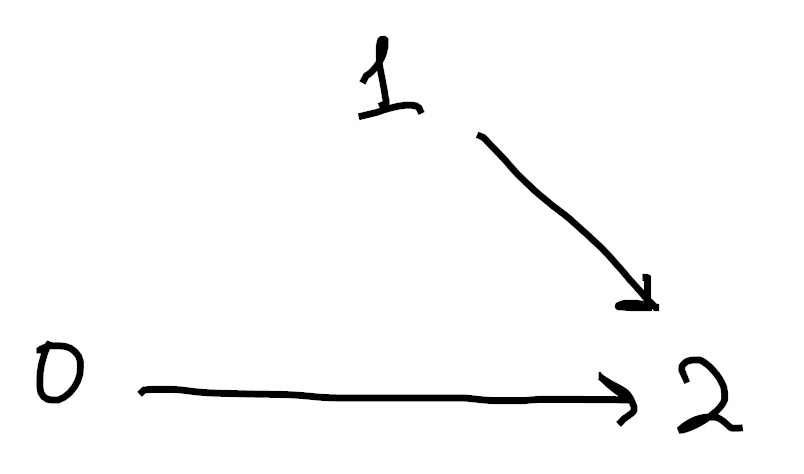
and we get $Λ_{2}^{2}$ by removing the interior 2-cell and the 1-cell opposite $2$ :

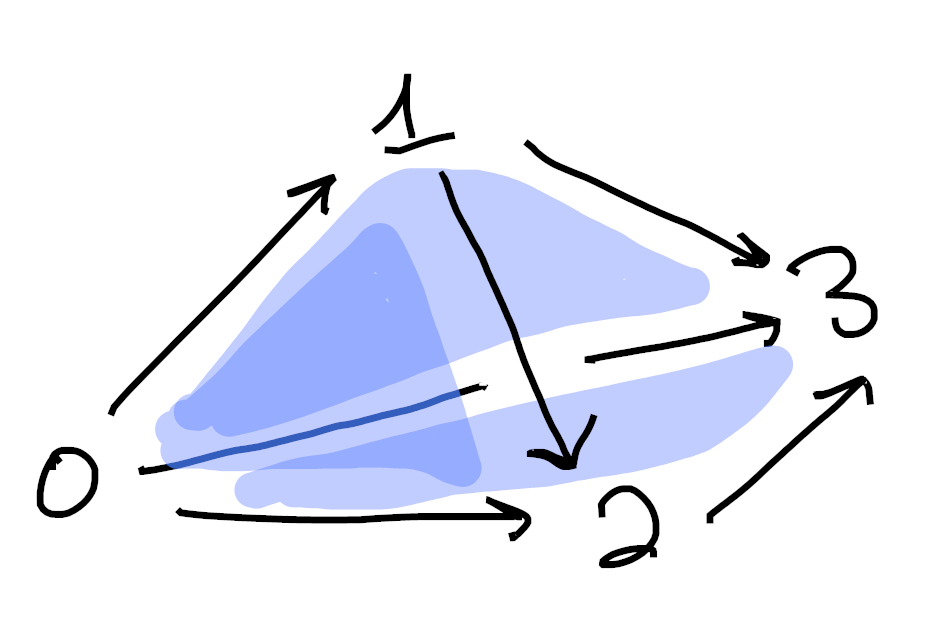
What about the horns of $Δ^{3}$ ? Well now, we remove the interior 3-cell (the “volume” of the simplex) as well as the 2-cell opposite your favorite vertex. Concretely, we see $Λ_{0}^{3}$ is given by²

Similarly, $Λ_{1}^{3}$ is

$Λ_{2}^{3}$ is

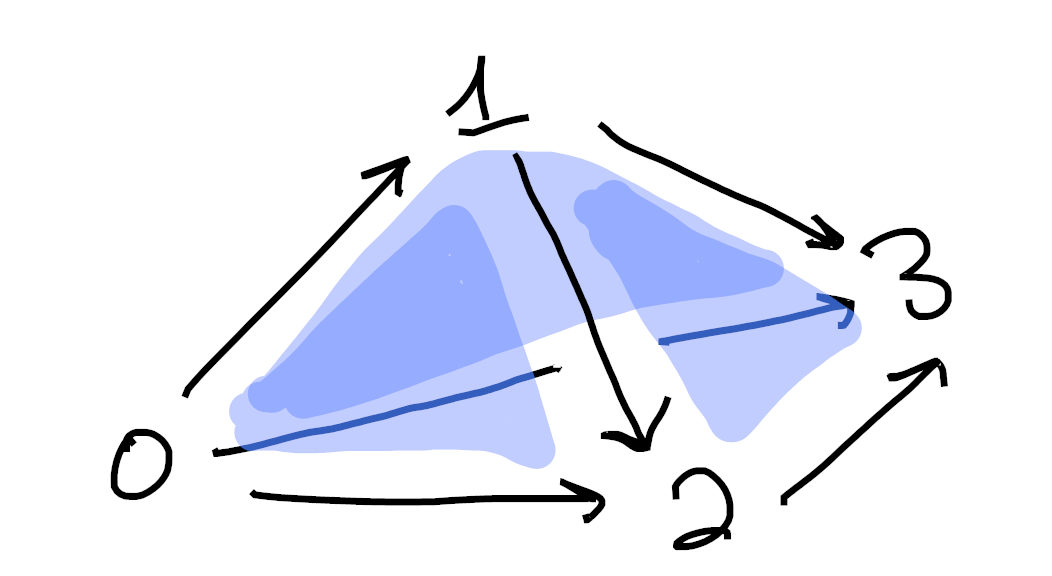
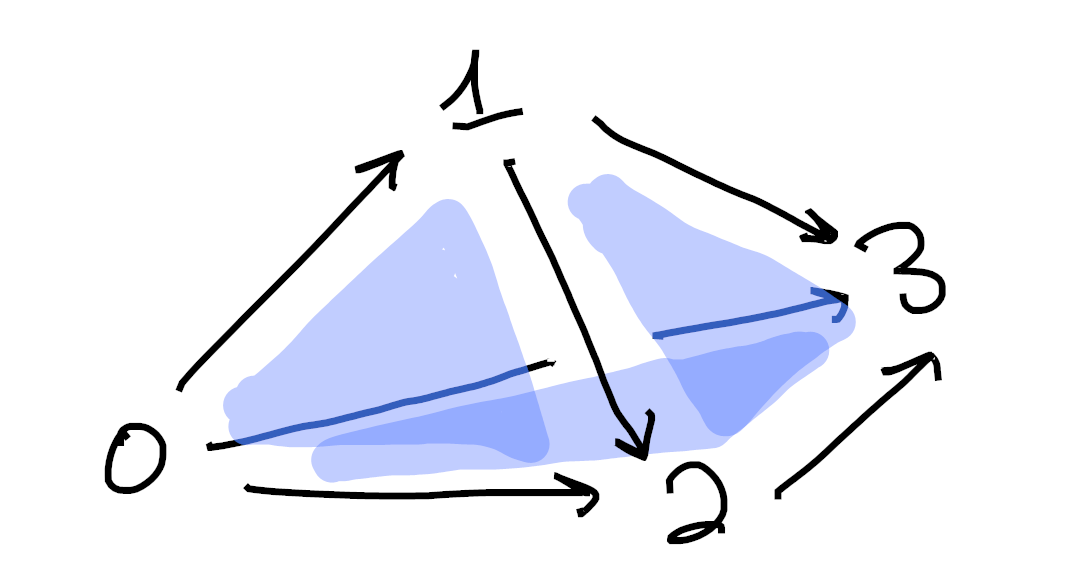
and $Λ_{3}^{3}$ is

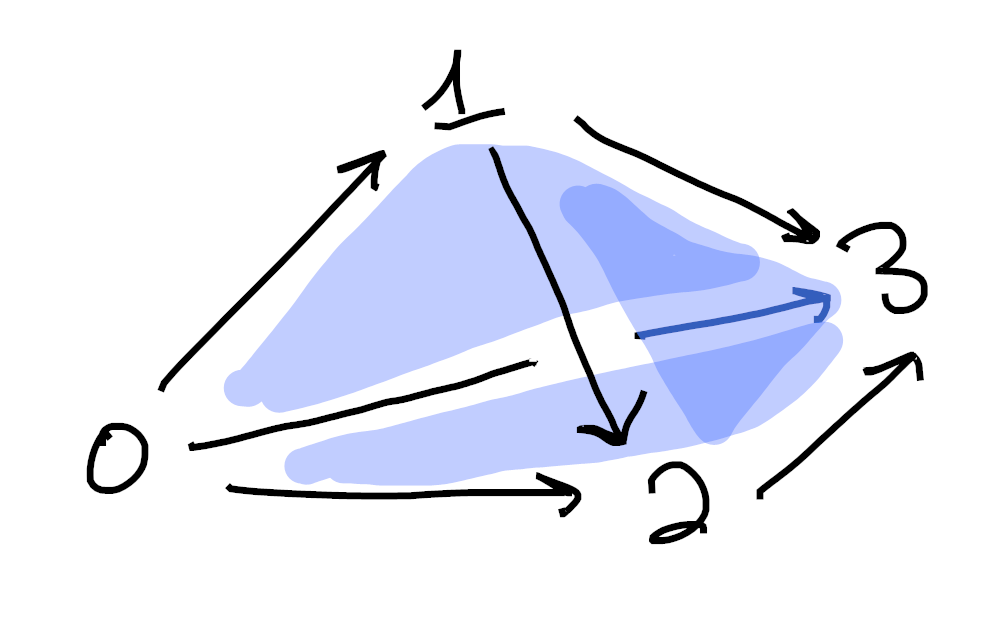
As a (quick?) exercise, you should try to write down a definition of $Λ_{i}^{n}$ as a simplicial set.

Remember that, by the yoneda lemma, it (more or less) suffices to say what the $k$ -cells are for each $k$ ³.

Now then, we come to an important definition

A simplicial set $X$ is called a Kan Complex if every horn $Λ_{i}^{n}$ in $X$ can be “filled” by a $Δ^{n}$ .

In a commutative diagram, we ask that the following dotted morphism should always exist:

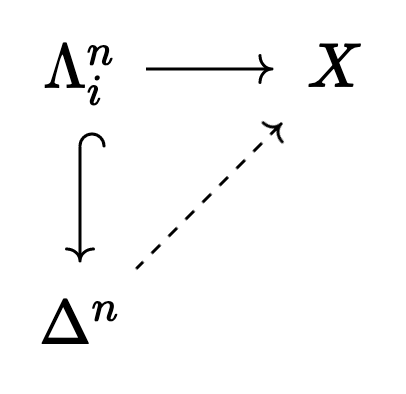
Why care about this? Because of the following major theorem:

For every topological space $X$ , ${Sing}_{X}$ is a kan complex.

Moreover, (up to weak equivalence), every kan complex arises in this way.

So we see that we can completely recover the notion of topological space (up to homotopy) by looking at special simplicial sets… But wasn’t this all supposed to have something to do with category theory?

Just like every topological space $X$ defines a simplicial set ${Sing}_{X}$ , every category also defines a simplicial set, called the Nerve of the category $C$ .

In general, the $n$ -cells in the nerve $N (C)$ will be given by the “paths” of length $n$ made of arrows in $C$ . That is

The 0-cells will be objects of $C$
The 1-cells will be the arrows, $C_{0} \to C_{1}$
The 2-cells will be the paths of length 2, $C_{0} \to C_{1} \to C_{2}$
The 3-cells will be the paths of length 3, $C_{0} \to C_{1} \to C_{2} \to C_{3}$
etc.

Concretely, let’s look at the following category (where $k = h f = h g$ ):

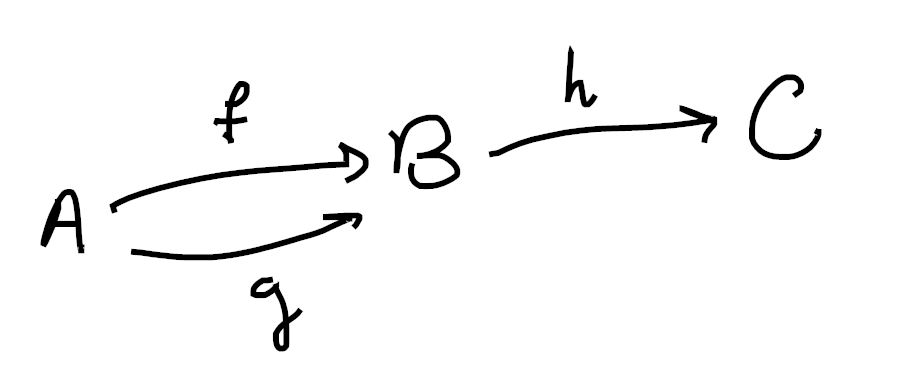
Then its nerve should have three 0-cells ( $A$ , $B$ , and $C$ ), plus 1-cells for $f$ , $g$ , $h$ , and the composite $k$ (notice this is only one 1-cell, since it’s a single arrow in $C$ ). However, we add two 2-cells:

A \overset{f}{\to} B \overset{h}{\to} C

A \overset{g}{\to} B \overset{h}{\to} C

since $k$ arises as a composite in two ways: $h f$ and $h g$ .

Thus, the nerve of $C$ is a cone

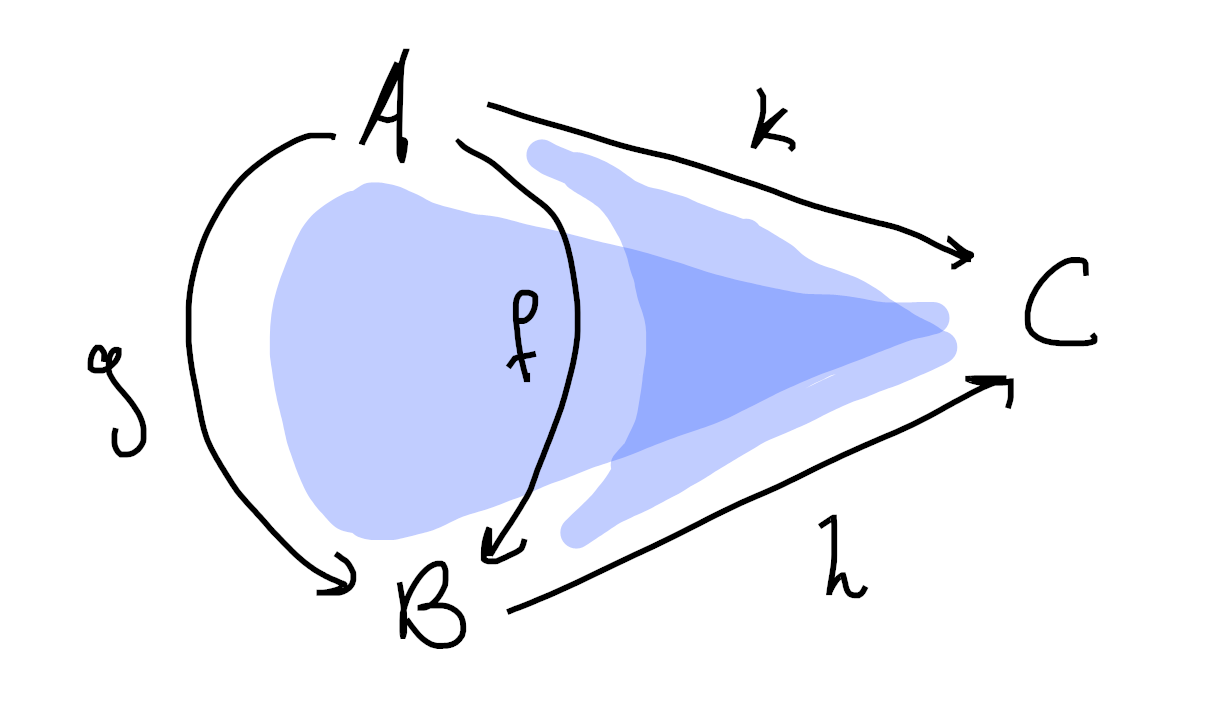
Perhaps a better way to visualize this is as a disk instead:

Of course, it’s easy to guess the next question. Can we tell which simplicial complexes arise as the nerve of some category?

Again, the answer is yes, and the answer will look shockingly similar to the case of topological spaces!

A simplicial complex is called a Quasicategory if every “inner horn” has a fill.

That is, every horn $Λ_{i}^{n}$ should have a fill, except when $i = 0$ or $i = n$ .

This should make sense as a definition, since in a category composition tells us that we can fill inner horns!

Indeed, consider the inner horn $Λ_{1}^{2}$ :

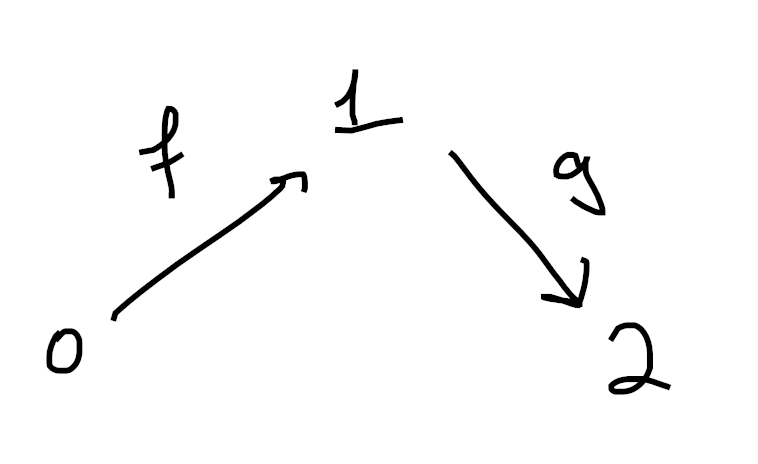
If this diagram lives inside the nerve of a category $N (C)$ , then we can always fill the horn! Indeed, we have a 1-cell from $0 \to 2$ given by $g f$ . We also have a 2-cell filling this triangle given by the path $0 \overset{f}{\to} 1 \overset{g}{\to} 2$ .

As a cute exercise, you should check that the two inner horns $Λ_{1}^{3}$ and $Λ_{2}^{3}$ have fills in the nerve of a category.

This all brings us to another major theorem:

For every category, the nerve $N (C)$ is a quasicategory.

Moreover, if $X$ is a quasicategory where each inner horn has a unique fill, then $X$ is isomorphic to the nerve of some category.

Moreover again, the nerve construction embeds the category of categories fully and faithfully into the category of quasicategories.

Importantly, this means that every kan complex is a quasicategory! This tells us that quasicategories allow us to treat spaces and categories on equal footing⁴!

In particular, quasicategories give us a setting where we can “do homotopy theory” to categories, and if you remember back to the main post about $\infty$ -categories, and how they solve the formal issues with model categories, that’s exactly what we were looking for!

Here’s another tentative definition. If this reminds you of the tentative definition of a “homotopy theory” from the last post, you have good instincts.

An $\infty$ -category is a quasicategory, where we say two quasicategories present the same $\infty$ -category if they are homotopy equivalent as simplicial sets.

This is great because it gives us a super concrete way of working with $\infty$ categories.

In this framework, our categories literally are geometric objects! The category of simplicial sets is a topos, so it has as many nice constructions as we could want, and many of these preserve kan complexes and quasicategories.

For instance, now functors are just simplicial maps, many limits and colimits of quasicategories can be computed as with geometric objects, exponentials give us functor quasicategories, and all of these work as well as we could hope.

Because of this concreteness, Jacob Lurie’s tomes on $\infty$ -categories are primarily based on the language of quasicategories. But in the main post, we defined an $\infty$ -category to be a category enriched in spaces…

How can we reconcile these viewpoints? Is there a way for us to apply the machinery proven in Lurie’s books to the hammock localization of a model category? Is there some way for us to use these nice geometric definitions for computations involving quasicategories, and leverage them to understand the simplicial categories we’ve been talking about? Why have we given two seemingly unrelated definitions of an $\infty$ -category in the first place?

For answers to these questions and more, read on to the last post in this series⁵!

Super concretely, given $n + 1$ vertices
$0 < 1 < \dots < n - 1 < n$
the $i$ th horn $Λ_{i}^{n}$ is $Δ^{n}$ minus two cells:
- the unique $n$ -cell
- the unique $n - 1$ cell which doesn’t contain $i$
↩
Sorry if these are hard to understand. Drawing 3d pictures is hard, haha. Each image is made up of 1-cells (colored in black) as well as 2-cells (shaded in blue). Moreover, in each picture we’ve omitted exactly one 2-cell from the boundary of the tetrahedron. ↩
If it’s not clear what role yoneda plays in this situation, see my answer here.

It’s also definitely worth reading Friedman’s An Elementary Illustrated Introduction to Simplicial Sets (avaialable here). ↩
I originally put this in the main body, but I ended up deciding it ruined the flow of the post too much. That said, I still think it’s a fun (and enlightening) example, so I wanted to include it as a ~bonus exercise~ here:

Show that two isomorphic categories give rise to homeomorphic nerves (after taking geometric realizations, of course).

Then, show that two equivalent categories give rise to homotopy equivalent nerves.

↩
Thank goodness! I have been working on these for so long. I really didn’t realize how big a project I was in for when I decided to make a post clarifying the relationship between model categories and $\infty$ -categories…

I love how it’s turning out, but I’m so ready for these posts to be behind me, haha. I also didn’t want to post any of them until they were all done. In part because I spent a lot of time moving various bits back and forth between posts, and once one is public I would want to consider it (mostly) set in stone. But also because I wanted to make sure I actually finished them all.

I have a bad habit of starting a series and leaving things unfinished (rest in peace cohomology part 1), but it was important that I not do that to these posts. ↩