A Quick Application of Model Categories

22 Mar 2023

Almost exactly a year ago (time flies!) I was thinking really hard about model categories in preparation for the HoTTEST summer school. I learned a TON doing this, but I’ve just today seen a really nice (and somewhat concrete) reason to care about the whole endeavor! I’d love to share it ^_^

Also, I know the blog posts have been slow lately. I have a handful of bigger posts in the pipeline that I really want to finish up as soon as I find the time. One is on 2-categories and what kinds of problems they solve (with a little appendix on an application of 3-categories), and another is on various ways of understanding categories. A category is simultaneously a geometric, logical, algebraic, set theoretic, etc. object, and this is part of what makes category theory so interesting and useful… but also so hard to learn! This post will break down all the ways I know of to think about categories, and why these different perspectives are useful. The 2-category post is likely to come out fairly soon, but the post on different perspectives is liable to take longer, haha. Still, I think they’ll both be good posts, so I’m excited to get them finished.

As long as we’re giving little life updates, I’m going to two conferences next week: The ASL general meeting in Irvine (where I’ll get to hang out with other logicians again! Actually, one of my best friends Pedro Marun is giving a talk on Tuesday, which I’m looking forward to) as well as a geometric group theory conference at UC Riverside. I’m going to have to split my time between the two conferences, since they perfectly overlap, but I really want to go to both. Thankfully Irvine and Riverside are only a 2 hour trainride apart!

There’s a paper of mine that’s been literally written, and just needs some revision, since august of last year. I want to talk about it with people at the geometric group theory conference, which means I should try to finish it this week… I’ll take a day and so that soon, but I’m running out of week, haha.

Ok, that’s enough about my life. Let’s get into the math!

---

First, let’s have a brief reminder of what a model category is. This is likely to be slightly ahistorical, since I’m optimizing for pedagogy rather than a correct timeline.

In $\mathsf{Top}$, the category of topological spaces, we find that continuous maps are often the wrong thing to study, in part because there’s too many. We can cut down on this by considering continuous functions “up to homotopy”, and when we do this we get a new category $\mathsf{hTop}$ which is as badly behaved as it is useful.

Mathematicians developed lots of tools for studying this category by working in (the much better behaved) $\mathsf{Top}$ for as long as possible, then quotienting out the homotopy relation at the very end.

Algebraically, we have the derived category of Grothendieck’s school. Here we have a notion of “chain homotopy” and again we want to consider not all chain maps, but merely chain maps up to homotopy. Again, the derived category is badly behaved, so we want to make computations in (the much better behaved) category of chain complexes for as long as possible, and quotient at the end.

There are many informal analogies between these two settings, morally mediated by the functor assigning to a topological space $X$ its “singular chain complex” ${\text{Sing}}_{\bullet }(X)$. Then homotopy in the topological setting becomes homotopy in the chain complex setting. Quillen made this analogy precise by distilling the common techniques between these two settings into the axioms for a model category. Now we know if we have a category $\mathcal{C}$ that admits a model structure, many of the techniques for working “up to homotopy” are immediately applicable to working with objects of $\mathcal{C}$ up to homotopy!

The only axiom I’ll mention here is the “lifting” axiom. It says that whenever we have a situation:

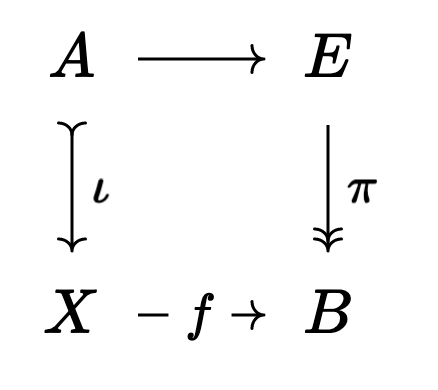
where $\iota$ is a cofibration, $\pi$ is a fibration, and at least one of the two is a weak equivalence, then we can always find a lift:

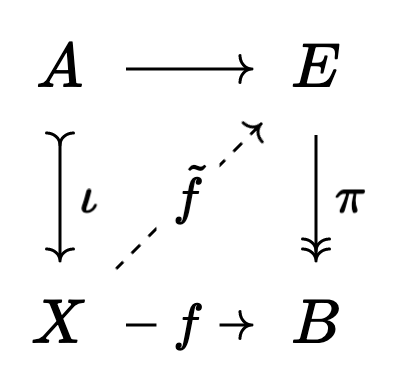
making the square commute.

---

Now, this is great and all, but what does it do for us? I’m happy with the ability to generalize old arguments to new settings, and model categories are very useful in modern mathematics for exactly this reason. But if we have a good abstract framework it should do more than just generalize! It should also recast old results in a way that’s easier to understand. After all, in the right level of generality, there’s often only one obvious thing to try!

And this is what prompted me to write this post. Earlier today I was reading Kottke’s notes on bundles (available here), which led me to a slightly surprising theorem in the comments of a mse question (which, in hindsight, I think I’ve seen before):

The key idea is that it’s easy to build maps into a contractible space¹, so contractible fibres make it easy to build a section of $\pi$. But how do we make this idea precise?

Here’s two proofs, which do two different things.

$⌜$ Proof 1:

Fix a CW structure on $B$. We’ll build the map $B\to E$ inductively.

First, to each $0$-cell $x$ in our structure, we’ll choose a point in the fibre over $x$.

Next, we want to say that for each $1$-cell in our structure (a path $x$ to $y$ between two $0$-cells) we can extend this map to the whole $1$-cell. One can show that this extension always exists.

Next, we say for each $2$-cell in our structure (a disk whose boundary is built from $1$-cells) we can extend this map to the $2$-cell. Again, one can show this always exists.

In general, inductively assume we’ve defined a map $B^{(k)}\to E$ from the $k$-skeleton of $B$ to $E$. We would like to extend this map to the $(k+1)$-skeleton. One can show that the function extends to a $(k+1)$ cell exactly when its image, restricted to the boundary of our cell, is nullhomotopic. But we use our contractibility assumption here in order to show that this condition always holds, so that we can always extend our function!

Along the way, we must be careful to make sure that our extension is always a section of $\pi$ at each step, but again this is doable.

If you believe all this, then the union of these partial sections $s^{(k)}$ is the desired global section $s:B\to E$. $⌟$

This proof is great because it really lets you feel like you understand what the section is. After all, it gives us a (somewhat complicated) procedure for building it²! The downside, of course, is all of the little technical details (all of which I glossed over). It feels like a fairly delicate inductive construction, and it would be great if there were a faster, more conceptual, proof. Enter model categories!

$⌜$ Proof 2:

Since $B$ is a CW complex, the unique map $\mathrm{\varnothing }\to B$ is a cofibration. Since $\pi :E\to B$ is a fibre bundle, it’s a fibration.

So we have a square

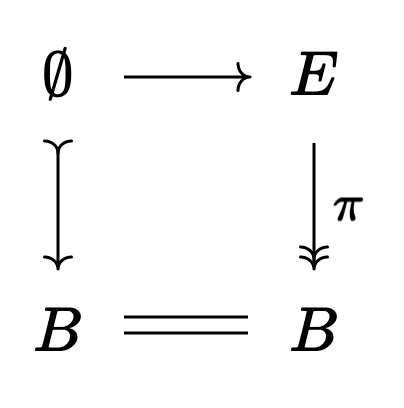
whose left side is a cofibration and whose right side is a fibration. Then, by the axiom we mentioned earlier, if we can show one of our arrows is a weak equivalence we’ll be able to fill this square:

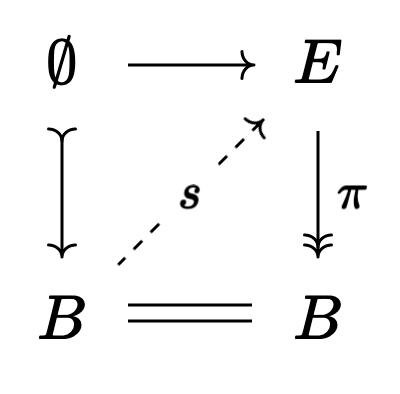
and commutativity of this diagram says that $\pi s={\text{id}}_B$ so that $s$ is a section of $\pi$!

There’s no way that $\mathrm{\varnothing }$ is going to be weakly equivalent to $B$, so we need to show that $\pi$ is a weak equivalence. That is, we need to show that the maps on homotopy groups (sorry in advance for this notation)

$${\pi }_n(\pi ):{\pi }_n(E)\to {\pi }_n(B)$$

should all be isomorphisms.

Now the long exact sequence of a fibration tells us

$$\cdots \to {\pi }_n(F)\to {\pi }_n(E)\to {\pi }_n(B)\to {\pi }_{n-1}(F)\to \cdots$$

But each ${\pi }_k(F)=0$ since our fibres are contractible! Thus our long exact sequence becomes $0\to {\pi }_n(E)\to {\pi }_n(B)\to 0$ and we get the desired isomorphisms. So $\pi$ is a weak equivalence, and the lifting axiom gives us our desired section. $⌟$

This proof is nice because it’s very conceptual. Provided you’re comfortable with long exact sequences, the proof is much less fiddly than the previous inductive proof, so there’s less that can go wrong along the way. The downside, of course, is that it makes it less clear what our section “really is”, since we don’t have to build it ourselves.

I wouldn’t be surprised if there’s a fiddly inductive proof involved in the proof that $\mathsf{Top}$ really does satisfy the model category axioms (in particular this lifting axiom), but that’s part of the beauty of theories like this! By packaging these technical proofs into a single (easy to use) set of axioms, we’re able to make future proofs less error prone! We get the technical work out of the way up front and all at once so that future mathematicians will have an easier time.

This is analogous to building a nice API for the theory. Lots of work went on behind the scenes, but now we can use that work without needing to check ourselves that $\mathsf{Top}$ really is a model category! But to use it, we need to know that the API exists. So it’s useful to learn the language of model categories even if we aren’t interested in the vast generalization of homotopy theory to other categories.

---

Thanks for reading! In hindsight, this is slightly less “down to earth” than I originally thought it was, haha. I’ve been doing math for far too long and it’s rotted my brain a little bit.

That said, hopefully the takeaway is clear. By packaging a fiddly proof into an axiom, we’re able to work with the cleaner axiom directly, rather than having to do a fiddly inductive proof ourselves! This is one way for the model category axioms to justify themselves. The fact that these axioms are satisfied for other categories as well can be thought of as icing on the cake!

This was a super quick one (I think I wrote it in under two hours, which is unheard of for me) because I really wanted to get it out before I do a bunch of other, more pressing work. This was helpful as well, because it means I allowed myself to not look too deeply into the details of proof $1$. I don’t fully understand it (and that probably shows from my sketch) but I think that’s ok. One of these days I’ll get around to learning some obstruction theory, and at that point I’ll come back to the proof with a better appreciation for just how fiddly the induction is ^_^.

Stay warm, everyone. Talk soon!

---