A Quick Application of Model Categories
22 Mar 2023
Almost exactly a year ago (time flies!) I was thinking really hard about model categories in preparation for the HoTTEST summer school. I learned a TON doing this, but I’ve just today seen a really nice (and somewhat concrete) reason to care about the whole endeavor! I’d love to share it ^_^
Also, I know the blog posts have been slow lately. I have a handful of bigger posts in the pipeline that I really want to finish up as soon as I find the time. One is on 2-categories and what kinds of problems they solve (with a little appendix on an application of 3-categories), and another is on various ways of understanding categories. A category is simultaneously a geometric, logical, algebraic, set theoretic, etc. object, and this is part of what makes category theory so interesting and useful… but also so hard to learn! This post will break down all the ways I know of to think about categories, and why these different perspectives are useful. The 2-category post is likely to come out fairly soon, but the post on different perspectives is liable to take longer, haha. Still, I think they’ll both be good posts, so I’m excited to get them finished.
As long as we’re giving little life updates, I’m going to two conferences next week: The ASL general meeting in Irvine (where I’ll get to hang out with other logicians again! Actually, one of my best friends Pedro Marun is giving a talk on Tuesday, which I’m looking forward to) as well as a geometric group theory conference at UC Riverside. I’m going to have to split my time between the two conferences, since they perfectly overlap, but I really want to go to both. Thankfully Irvine and Riverside are only a 2 hour trainride apart!
There’s a paper of mine that’s been literally written, and just needs some revision, since august of last year. I want to talk about it with people at the geometric group theory conference, which means I should try to finish it this week… I’ll take a day and so that soon, but I’m running out of week, haha.
Ok, that’s enough about my life. Let’s get into the math!
First, let’s have a brief reminder of what a model category is. This is likely to be slightly ahistorical, since I’m optimizing for pedagogy rather than a correct timeline.
In
Mathematicians developed lots of tools for studying this category by working
in (the much better behaved)
Algebraically, we have the derived category of Grothendieck’s school. Here we have a notion of “chain homotopy” and again we want to consider not all chain maps, but merely chain maps up to homotopy. Again, the derived category is badly behaved, so we want to make computations in (the much better behaved) category of chain complexes for as long as possible, and quotient at the end.
There are many informal analogies between these two settings, morally mediated
by the functor assigning to a topological space
A Model Structure on
- The Weak Equivalences
- The Fibrations
- The Cofibrations
satisfying certain axioms.
We think of a weak equivalence as an “isomorphism up to homotopy”, a fibration as a “homotopically nice surjection” and a cofibration as a “homotopically nice inclusion”.
You can read more in an old blog post of mine, which also gives plenty of references if you’re interested in learning more!
The only axiom I’ll mention here is the “lifting” axiom. It says that whenever we have a situation:
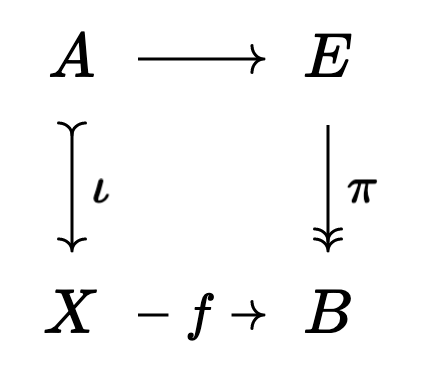
where
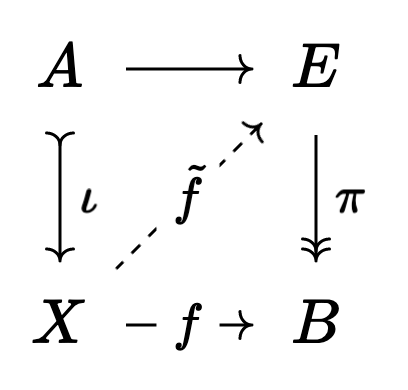
making the square commute.
Now, this is great and all, but what does it do for us? I’m happy with the ability to generalize old arguments to new settings, and model categories are very useful in modern mathematics for exactly this reason. But if we have a good abstract framework it should do more than just generalize! It should also recast old results in a way that’s easier to understand. After all, in the right level of generality, there’s often only one obvious thing to try!
And this is what prompted me to write this post. Earlier today I was reading Kottke’s notes on bundles (available here), which led me to a slightly surprising theorem in the comments of a mse question (which, in hindsight, I think I’ve seen before):
If
The key idea is that it’s easy to build maps into a contractible space1,
so contractible fibres make it easy to build a section of
Here’s two proofs, which do two different things.
Fix a CW structure on
First, to each
Next, we want to say that for each
Next, we say for each
In general, inductively assume we’ve defined a map
Along the way, we must be careful to make sure that our extension is always
a section of
If you believe all this, then the union of these partial sections
This proof is great because it really lets you feel like you understand
what the section is. After all, it gives us a (somewhat complicated)
procedure for building it2! The downside, of course, is all of the
little technical details (all of which I glossed over). It feels like a
fairly delicate inductive construction, and it would be great if there were a
faster, more conceptual, proof. Enter model categories!
Since
So we have a square
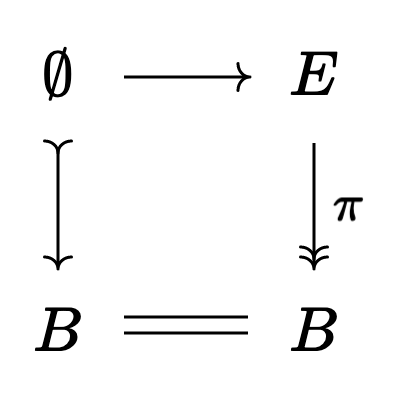
whose left side is a cofibration and whose right side is a fibration. Then, by the axiom we mentioned earlier, if we can show one of our arrows is a weak equivalence we’ll be able to fill this square:
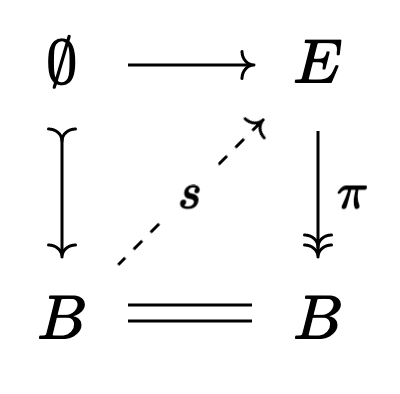
and commutativity of this diagram says that
There’s no way that
should all be isomorphisms.
Now the long exact sequence of a fibration tells us
But each
This proof is nice because it’s very conceptual. Provided you’re comfortable
with long exact sequences, the proof is much less fiddly than the previous
inductive proof, so there’s less that can go wrong along the way.
The downside, of course, is that it makes it less clear what our section
“really is”, since we don’t have to build it ourselves.
I wouldn’t be surprised if there’s a fiddly inductive proof involved in
the proof that
This is analogous to building a nice API for the theory. Lots of work
went on behind the scenes, but now we can use that work without needing to
check ourselves that
Thanks for reading! In hindsight, this is slightly less “down to earth” than I originally thought it was, haha. I’ve been doing math for far too long and it’s rotted my brain a little bit.
That said, hopefully the takeaway is clear. By packaging a fiddly proof into an axiom, we’re able to work with the cleaner axiom directly, rather than having to do a fiddly inductive proof ourselves! This is one way for the model category axioms to justify themselves. The fact that these axioms are satisfied for other categories as well can be thought of as icing on the cake!
This was a super quick one (I think I wrote it in under two hours, which is
unheard of for me) because I really wanted to get it out before I do a bunch
of other, more pressing work. This was helpful as well, because it means I
allowed myself to not look too deeply into the details of proof
Stay warm, everyone. Talk soon!
-
This idea forms the beginning of obstruction theory. I would love to know more about this, but I haven’t had the time to really look into it. ↩
-
As an aside, I would be curious how constructive the obstruction theory here is. Given a function on the