Preprint -- The RAAG Functor as a Categorical Embedding

05 Oct 2023 - Tags: my-preprints

After almost a year of sitting on my hard drive, I finally had time in August to finish revising my new preprint on Right Angled Artin Groups (Raags). And in September I had time to put it on the arxiv for people to see! Within 24 hours I had an email from somebody who had read it, and was interested in reading it closely! It’s super exciting to see that people are actually reading something I wrote, and it’s really validating to feel like the math I did last year was worth it ^_^. In this post, I’d love to give a quick informal description of what’s going on in that paper.

First, what’s a right angled artin group? We’ve actually talked about them before in the second ever post on this blog (!) but here’s a quick tl;dr.

Fix a (simple, undirected) graph $Γ$ with underlying vertex set $V$ .

The Right Angled Artin Group $A Γ$ is the group

⟨ v \in V ∣ [v_{1}, v_{2}] for {v_{1}, v_{2}} \in Γ ⟩

freely generated by the vertices, where two vertices commute if and only if they’re adjacent in $Γ$ .

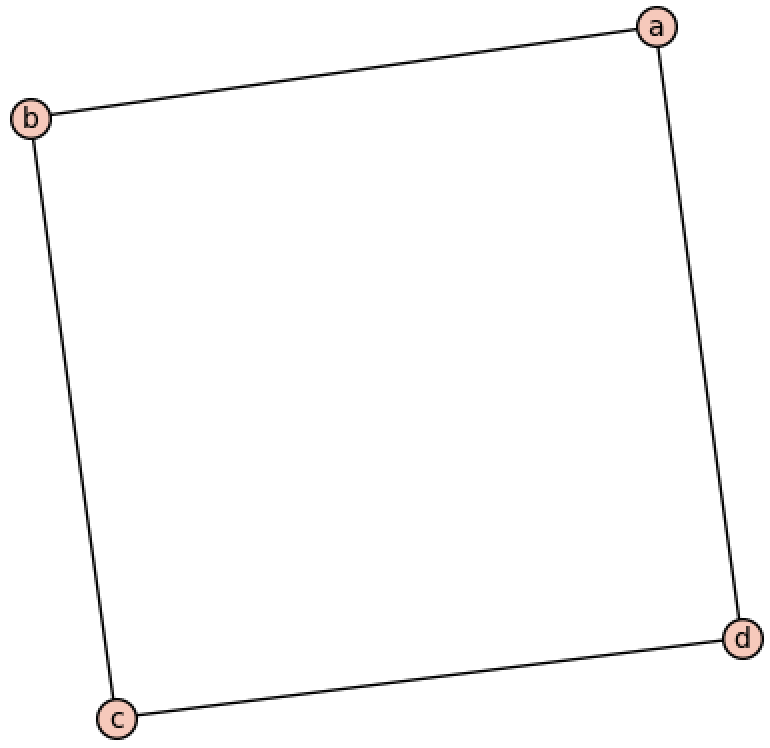
For example, in case $Γ$ is a complete graph on $n$ vertices, $A Γ$ is a free abelian group of rank $n$ . If $Γ$ has no edges, then $A Γ$ is a free group of rank $n$ . As a quick exercise, can you convince yourself that for $Γ$ as below, we have $A Γ ≅ F_{2} \times F_{2}$ is a direct product of free groups?

Now, it’s not hard to see that the right angle artin group construction $A$ is actually a functor $A : Gph \to Grp$ from the category of graphs to the category of groups. After all, if $φ : Γ \to Δ$ is a graph homomorphism¹ then we get a group homomorphism $A φ : A Γ \to A Δ$ given by sending each generator $v \in A Γ$ to the generator $φ v \in A Δ$ .

Moreover, $A : Gph \to Grp$ admits a right adjoint! This makes precise the idea that the raag on $Γ$ is a kind of “free group” associated to $Γ$ . Given a group $G$ , we define its Commutation Graph $C G$ to be the graph² whose vertices are elements of $G$ where $g_{1}, g_{2} \in C G$ is an edge if and only if $g_{1}$ and $g_{2}$ commuted in $G$ .

This allows us to bring much more powerful category theory to the table. In particular, it lets us use the machinery of comonadic descent to characterize the essential image of $A$ . That is, to understand which groups are raags, and to understand which homomorphisms between raags are $A φ$ for some graph homomorphism! In fact, we show that $A$ is a categorical embedding, so that $Gph$ is a (non-full) subcategory of $Grp$ !

Moreover, the characterization is something we can really calculate with!

The main theorem of the paper states that there is a coalgebra structure we can put on groups so that

The coalgebra structures on a group $G$ are in bijection with the graphs $Γ$ so that $G ≅ A Γ$
A homomorphism $f : G \to H$ respects this coalgebra structure if and only if $f = A φ$ for a graph homomorphism.

In particular, the raags are exactly the groups admitting such a coalgebra structure.

One thing that I wish more mathematicians would talk about is the kind of meandering nature of research. When you see a paper written in defnition-theorem-proof style, it’s hard to imagine what the discovery process must have looked like. It’s almost always much messier than the final paper would lead you to believe, so I want to take a minute to talk about the history of this paper.

Why was I thinking about all this?

There’s an important open question in the theory of raags about the “nonstandard” embeddings between two raags.

Obviously if $Γ$ is a (full) subgraph of $Δ$ , then $A Γ$ is a subgroup of $A Δ$ in a canonical way. But it turns out we can have pairs so that $A Γ$ embeds into $A Δ$ , but $Γ$ is not a subgraph of $Δ$ ! Motivated by questions in geometric group theory, it’s natural to want to understand when these “nonstandard” embeddings are possible.

Now the adjunction comes into play. If we have an embedding $A Γ \to A Δ$ , then our adjunction gives us a map of graphs $Γ \to C A Δ$ . Since $C A : Gph \to Gph$ is a monad on the category of graphs, we (not very creatively) call this construction the Monad Graph of $Δ$ .

It would be nice to have a combinatorial characterization of when a map $Γ \to C A Δ$ transposes to an embedding $A Γ \to A Δ$ . But such a characterization is as yet unknown³.

I actually had most of these thoughts back in 2020 when I was first thinking about raags, but they didn’t really go anywhere. Especially since I was focused on life things like passing my quals and finding an advisor. But that all changed in 2022 when I started really trying to understand stacks…

One way to understand stacks⁴ is as “categories satisfying descent”. In the same way that a sheaf on $X$ assigns a set to each open in a way that elements of the set glue along open covers, a stack on $X$ assigns a category to each open in a way that objects and arrows of the category glue along open covers!

This story is closely tied up with the story of descent theory, so I took a detour through understanding that⁵. Along the way I found out about comonadic descent which (among other things) lets you characterize the image of a left adjoint. I remembered this raags adjunction that I worked on, and knew that its image was pretty easy to understand. Maybe the adjunction was comonadic and I could use this to attack the nonstandard embedding problem!

Once I knew the right question to ask, the proof itself was surprisingly simple, and I had a rough draft within a day or two⁶.

Next came the process of writing everything up in a way that doesn’t require a ton of category theoretic background. Working out the exposition for the paper was super enlightening for me⁷. Hopefully it also makes it more accessible for people new to the subject!

Ok, with the history out of the way, let’s talk about

What’s in the paper

This is pretty quick to outline, since I’m assuming a category theory background of my blog readers that I wasn’t assuming of my paper readers. That said, if it ever gets too heavy, feel free to read the first few sections of the paper, since I go into much more detail there.

The main result is implied by the categorical statement that the adjunction $A ⊣ C$ is Comonadic. This says that $Gph$ is equivalent to the category of $A C$ -coalgebras on $Grp$ , and moreover that the equivalence intertwice the adjunctions $A ⊣ C$ (on the $Gph$ side) and the co-free/forgetful adjunction (on the ${Grp}_{A C}$ side).

That is, we have a situation as below:

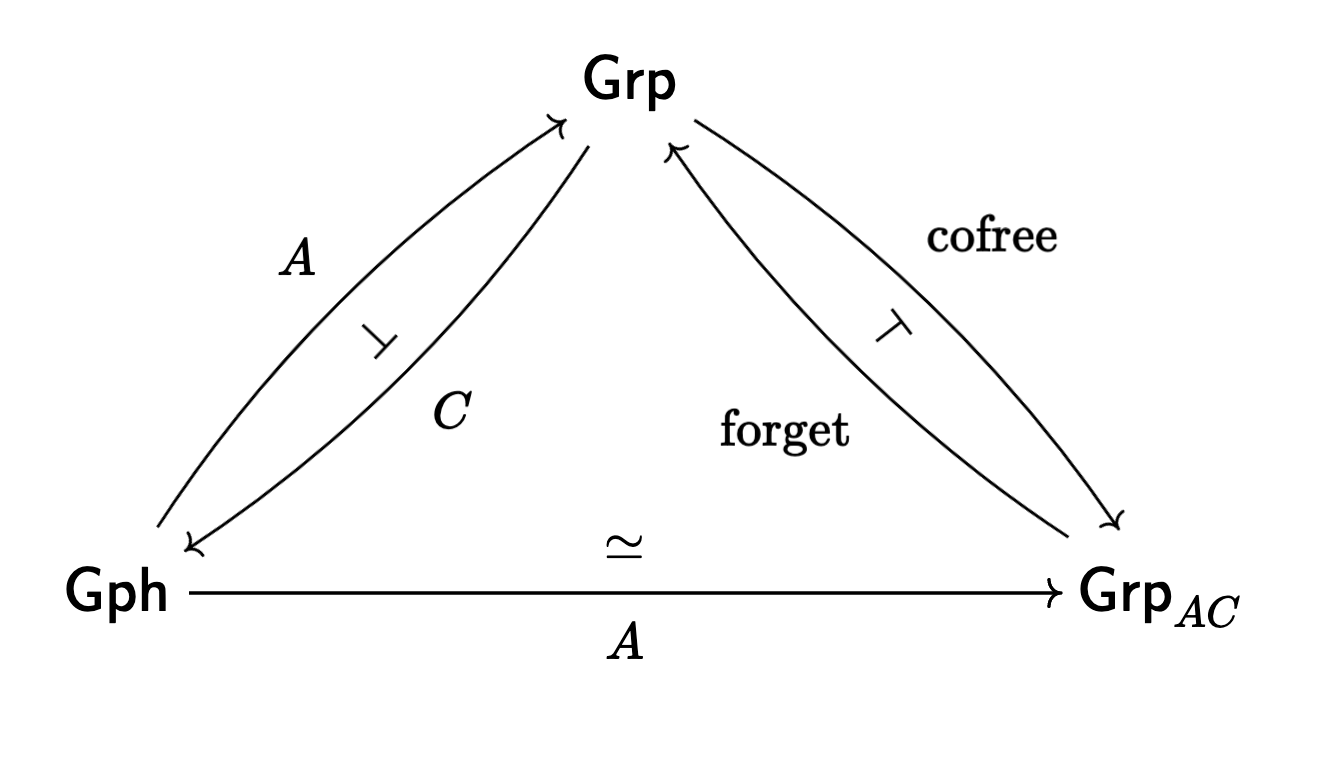
Really the equivalence $A$ sends a graph $Γ$ to the group $A Γ$ with the coalgebra structure $A η_{Γ} : A Γ \to A C A Γ$ , so that after forgetting this structure we get $A : Gph \to Grp$ .

How do we show that this really is an equivalence? The answer is Beck’s (Co)monadicity Theorem! It says that for any adjunction $A ⊣ C$ the base of that triangle is an equivalence if and only if $A$ reflects isomorphisms and preserves equalizers of “ $A$ -split parallel pairs”.

In the paper we use a different version of the comonadicity theorem which is easier to check, but it boils down to the same proof.

It’s “well known” in raag circles that $A$ is conservative (this can already be found in a 1987 paper of Droms), so we need to check that $A$ preserves certain equalizers. We can do this with a slightly technical argument of combinatorics on words. The key fact is that we have a good understanding of normal forms for the elements in $A Γ$ ⁸.

The last section of this paper was a small application of this machinery. We’re able to reprove a result that we can effectively recover $Γ$ from the isomorphism type of $G ≅ A Γ$ , as long as we’re promised that $G$ really is a raag⁹. We also show that if we have any concrete examples of groups $G$ with $A C$ -coalgebra structures, we can really do all the computations that we would want to do!

I think I like this format of blog posts putting more emphasis on the things that were on my mind when I was working on a paper, rather than the contents of the paper itself. Maybe if I write a more detailed paper I can say some informal words about what’s in it, but I think the historical perspective might help younger mathematicians see how messy research can be, and how incidental things can all blend together into a result. I just happened to be thinking about raags a few years before I happened to learn about stacks and descent, which opened the door to a result on descent for raags. Hopefully you all also like the historical perspective ^_^.

I’m also going to try to keep these paper announcement posts a bit less polished. It’s easy to get paralysis and revise posts forever and never finish them (ask me how I know…) I want to make sure that these actually get out, so I’ll try to keep them light on the revision. That shouldn’t be hard if the main point is the history!

Anyways, thanks for hanging out, all. I’m super excited to have a result, and I’ll be submitting to journals in the near future. Stay warm, and we’ll talk soon ^_^.

In the sense that $φ : V \to W$ is a function on the underlying vertices preserving the edge relation. So $v_{1}, v_{2} \in Γ$ implies $φ v_{1}, φ v_{2} \in Δ$ . ↩
In order to make this an honest adjunction, we need to require every vertex of our graph have a self loop. That is, we actually work with reflexive simple undirected graphs. This is a kind of technical point, since if every vertex has a self loop we don’t need to draw them! So the combinatorics remains basically unchanged. ↩
There’s reason to suspect this is a good idea, though! Not only is it category-theoretically natural, but (as far as I know) the best characterization of raag embeddings we have is due to Kim and Koberda, which shows that whenever $Γ$ embeds into their extension graph $Δ^{e}$ that $A Γ$ embeds into $A Δ$ . The interesting relationship is that $Δ^{e}$ is the full subgraph of $C A Δ$ on the conjugates of the generators!

In fact, Kim and Koberda conjectured that the converse is true too, so that $Δ^{e}$ is the right graph to consider to understand the nonstandard embeddings, but this was disproven in a 2013 paper of Casals-Ruiz, Duncan, and Kazachov. (Many thanks to Carl-Fredrik Nyberg-Brodda for telling me about this)

This is actually good news for my paper, since it means that we’ll want to understand more of the monad graph in order to better understand the embeddings, instead of being satisfied understanding a subgraph. ↩
And there are many! I want to write a blog post about them sometime soon. ↩
I was especially drawn to this because I learned that descent is closely related to monads. Even though objectively I’m very comfortable with monads nowadays, deep inside me there’s still a teenage programmer fascinated and confused by monads while learning haskell. It’s kind of wild to think that almost 10 years ago haskell launched me on my category theory journey. It’s even wilder to think of how far I’ve come since then! ↩
I once heard some advice that once you’ve climbed a high mathematical mountain (like geting some comfort with descent theory) it’s worth looking around to see if there’s anything else to do while you’re up there.

This led me to another question about understanding which essentially algebraic theories are secretly algebraic. This amounts to understanding the image of the left (2-)adjoint from finite product categories to finite limit categories.

I was actually able to work this out as well during CT2023, but unfortunately I learned while writing it up that Pedicciho and Wood had published the same result in ‘99. I was sad, of course, but I learned a TON while working on that project, about essentailly algebraic theories, locally finitely presentable categories, 2-categories, and lots more! That’s actually coming in super handy with my thesis project, since locally presentable categories are the target for factorization homology!

Again, research is a messy and winding road. ↩
For much the same reason that writing these blog posts is often good for me! Teaching is a great way to learn, and to make sure you really understand a subject. ↩
In fact, in multiple of these comonadicity proofs I’ve done, the key to checking this equalizer condition is an understanding of normal forms for the free objects!

This is yet another reason that the search for “normal form” theorems for various algebras is an incredibly useful pursuit! ↩
Determining whether or not a group $G$ is a raag, without being promised that it is one, is undecidable. ↩