Talk -- 2-Categorical Descent and (Essentially) Algebraic Theories

14 Nov 2023 - Tags: my-talks

A few weeks ago I gave a talk at the CT Octoberfest 2023 about some work I did over the summer that I’m really proud of. Unfortunately, while writing up the result I found a 1999 paper by Pedicchio and Wood that proves the same theorem (with roughly the same proof), so I wasn’t able to publish. Thankfully, the work is still extremely interesting, and I was more than happy to talk about it at a little online conference for other category theorists ^_^.

---

Recall an algebraic theory is something like groups, rings, modules, etc. It’s a structure that can be defined as a set (or possibly multiple sets) with some operations defined on it (allowing constants as $0$-ary operations) and equations specifying the behavior of those operations.

An essentially algebraic theory is something like categories. It’s a structure that can be defined as a set (or possibly multiple sets) with some operations defined on it, etc. The main superpower we get in the essentially algebraic world over the algebraic one is partially defined functions. Now our operations don’t have to be defined everywhere, they are allowed to be defined on subsets of the sorts. As long as those subsets are definable by equations!

For instance, the theory of categories is essentially algebraic since we have

• Sets $O$ and $A$ (the sets of objects and arrows)
• operations $\text{dom},\text{cod}:A\to O$ taking an arrow to its domain/codomain
• an operation $\text{id}:O\to A$ taking an object to the identity arrow at that object
• an operation $\circ :\{(f,g)\in A\times A\mid \text{dom}(f)=\text{cod}(g)\}$
• satisfying certain equational axioms, like $\text{dom}(\text{id}(x))=x=\text{cod}(\text{id}(x))$, $(f\circ g)\circ h=f\circ (g\circ h)$, etc.

Notice that composition isn’t defined on the whole set $A\times A$. It’s only partially defined! But the set where it’s defined is easy to understand – it’s defined by an equation in the other functions ($\text{dom}(f)=\text{cod}(g)$).

Contrast this with fields, which have a partially defined inverse operation $(-{)}^{-1}:\{x\in k\mid x\ne 0\}\to k$. There is no way to write the domain of inversion as an equation¹.

Now, essentially algebraic theories are extremely nice, for lots of reasons I outlined in my talk (and mentioned on the nlab page I linked earlier), but they’re not quite as nice as honest algebraic theories.

For instance, the underlying set of a quotient of groups is a quotient of the underlying set. If we have a surjection $G\twoheadrightarrow H$, then there’s an equivalence relation² $\theta$ on $UG$ (the underlying set of $G$) so that $UH\cong (UG)/\theta$.

This is no longer the case for models of an essentially algebraic theory! That is, the underlying set of a quotient might not be a quotient of the underlying set³.

For example, consider the following category:

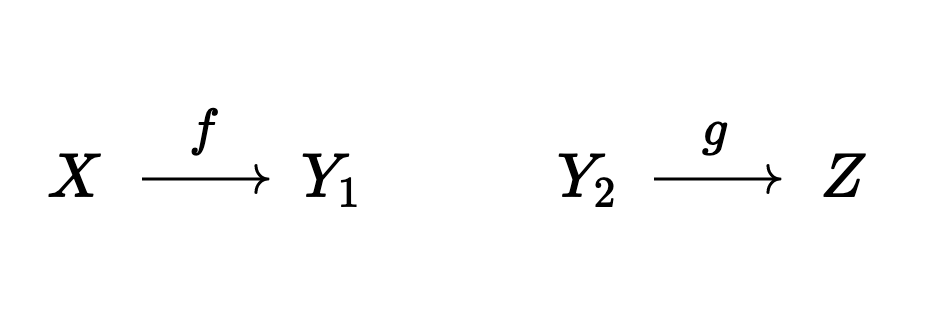
Notice its set of arrows (ignoring identities) is $f,g$.

Now if we quotient to set $Y_1=Y_2$, we get a new category

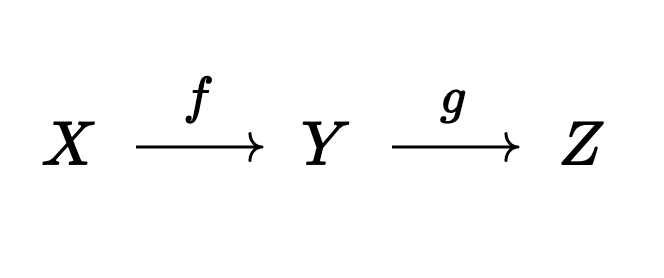
But now that $Y_1=Y_2$, $f$ and $g$ are composable! So we had better add a composite!

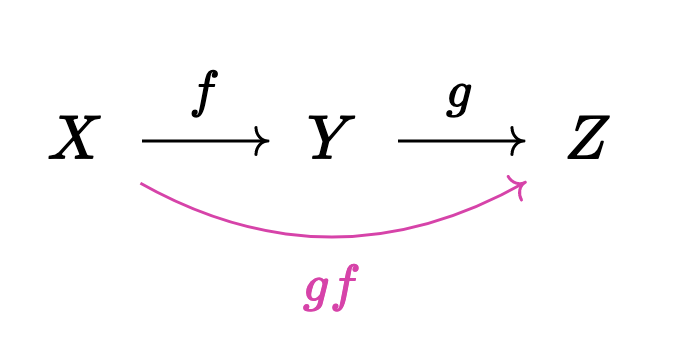
So after quotienting, our underlying set of arrows (again, ignoring identities) is $f,g,gf$, which isn’t a quotient of the set we started with! Also, note the role that partial operations played in this. The reason we got ~bonus elements~ in our underlying set is because after quotienting the domain for the partial operation got bigger, so we had to freely add stuff to make sure we were closed under composition.

Another reason to care about algebraic theories over essentially algebraic ones is that algebraic theories can be interpreted in any finite product category, while essentailly algebraic theories make use of all finite limts! This shows up even for “real mathematicians”, since the category $\mathsf{Diff}$ of smooth manifolds doesn’t have finite limits! So we can define a lie group as a group object in $\mathsf{Diff}$ (since the theory of groups is algebraic) but we can’t define a lie groupoid as a groupoid object in $\mathsf{Diff}$ (since the theory of groupoids is merely essentially algebraic)⁴!

With this in mind, it’s natural to ask when we can recognize an algebraic theory amongst the essentially algebraic ones. It turns out we can, and the process requires a fair amount of category theory!

---

We’ve already touched on the relationship between

• $$\{\text{algebraic theories}\}\leftrightsquigarrow \{\text{finite product categories}\}$$
• $$\{\text{essentially algebraic theories}\}\leftrightsquigarrow \{\text{finite limit categories}\}$$

But it turns out the relationship goes much deeper! Indeed, one can show that the “sets” in the above bullets actually represent $2$-categories, and that the correspondences are (contravariant) bi-equivalences!

Given a finite product (resp. finite limit) category $\mathcal{C}$, we treat it as an (essentially) algebraic theory, and say its category of models is the category of finite product (resp. finite limit) functors $\mathcal{C}\to \mathsf{Set}$.

In fact, we can go further! Given a finite product (resp. finite limit) categories $\mathcal{C}$ and $\mathcal{V}$, we say that the cateogry of $\mathcal{C}$ models in $\mathcal{V}$ is the category of finite product (resp. finite limit) functors $\mathcal{C}\to \mathcal{V}$.

Conversely, given a category of models for some (essentially) algebraic theory, its category of ($\mathsf{Set}$-valued) finitely generated free algebras⁵ (resp. finitely presented algebras) has finite coproducts (resp. finite colimits). So if we take the opposite category of this, we get a category with finite products (resp. finite limits)!

It’s then not so hard to show that these operations are mutually inverse⁶!

Now if we have an algebraic theory $\mathbb{A}$, that corresponds to a finite product category $\mathcal{A}$ where the category of $\mathbb{A}$-models is the functor category $\mathsf{FinProd}(\mathcal{A},\mathsf{Set})$.

To view this as an essentially algebraic theory, we want to find a finite limit category $\mathcal{E}$ which has the same models. That is, so that for every finite limit category $\mathcal{V}$:

$$\mathsf{FinLim}(\mathcal{E},\mathcal{V})\cong \mathsf{FindProd}(\mathcal{A},U\mathcal{V})$$

where $U$ is the forgetful functor from finite limit categories to finite product categories.

This makes it clear that $\mathcal{E}$ should be the free finite limit completion of the finite product category $\mathcal{A}$ we started with! Since we already have products, all we have to do is freely add equalizers!

With this in mind, we see how to rephrase our problem of recognizing the algebraic theories among the essentially algebraic ones!

Thankfully, there’s a very heavy hammer we can use to understand the image of a left adjoint: Comonadic Descent!

---

I don’t want to say too much about (co)monadic descent here, mainly because I’m going to a friend’s concert tonight and I’ve already written quite a lot about it in my recent preprint. But here’s the short story. We have a diagram of categories

where ${\mathsf{FinLim}}_{\mathsf{Eq}U}$ is the category of coalgebras for the $\mathsf{Eq}U$ comonad, and the usual Barr-Beck yoga shows that everything in the image of $\mathsf{Eq}$ has a canonical coalgebra structure, which is where the top map (which I’m abusively also calling $\mathsf{Eq}$) comes from.

The adjunction $\mathsf{Eq}⊣U$ is called comonadic exactly when this top map is an equivalence. In particular, this means we can recognize the image of $\mathsf{Eq}$ in $\mathsf{FinLim}$ as those categories admitting an $\mathsf{Eq}U$ coalgebra structure!

It turns out to not be too hard to prove that this adjunction is comonadic by using Beck’s famed (Co)monadicity Theorem! This comes down to some combinatorics⁷ involving Pitt’s explicit construction of the equalizer completion, first published in Bunge and Carboni’s The Symmetric Topos, which solves our problem!

Pedicchio and Wood, in their ‘99 paper A Simple Characterization of Theories of Varieties, give a nice characterization of the image of $\mathsf{Eq}$ as those categories with enough “effective projectives”⁸.

---

Let me say a quick word about the “2-categorical” in the title. In the last section, to make use of the descent machinery, we had to work with 1-categories $\mathsf{FinLim}$ and $\mathsf{FinProd}$. That is, with stict such categories. Of course, this result should really be 2-categorical in nature, working with all such categories, and we should be using a 2-categorical version of comonadic descent to prove the theorem… Unfortunately I don’t know of one!

I was kind of hoping that someone would ask about this during the talk – after all I put “2-categorical” in the title, but didn’t mention 2-categories at all! But my talk was the first talk of the day⁹, so it makes sense that people would have been nice and not asked that.

Regardless, I’m pretty sure an australian would have a reference for this kind of descent (and I might ask about it in the category theory zulip after posting this), because there’s no way I’m the first person to want to use it!

All in all, I’m happy with how the talk went. It was one of the shorter talks I’ve given, and I wanted to assume the audience didn’t know a ton of logic. I think I did a good job giving the flavor of the theorem, and some reasons to care about it, without necessarily getting bogged down in the details of the proof. Hopefully I didn’t come off as too upset that I was 24 years late to publish it myself!

As usual, here’s a copy of the slides, abstract, and recording. I’ll also encourage people to take a look at some of the other talks from the conference (which you can find here). There were a ton of interesting ones¹⁰ and if you like category theory I’m sure you’ll find something you enjoy!

Thanks again for reading. Stay warm, and try not to let the November darkness weigh on you too much! Talk soon ^_^

---

$2$-Categorical Descent and (Essentially) Algebraic Theories

An essentially algebraic theory is an algebraic theory that moreover allows certain partially defined operations. Since algebraic theories enjoy certain nice properties that essentially algebraic theories don’t, it’s natural to ask if we can recognize when an essentially algebraic theory is actually algebraic. In the language of functorial semantics, this amounts to recognizing when a finite limit category is the free completion of a finite product category, and the problem can be solved by considering a 2-categorical descent theory. This was independent work, but writing it up I learned that the same result can already be found in a 1999 paper of Pedicchio and Wood. This seems to be less well known than it should be, and I hope this talk brings attention to this fascinating subject.

The slides are here, and a recording is below:

---