Where Do Those Undergraduate Divisibility Problems Come From?
16 Jan 2025 - Tags: sage
Oftentimes in your “intro to proofs” class or your first “discrete math” class or something similar, you’ll be shown problems of the form “prove that for $n^6 + n^3 + 2n^2 + 2n$ is a multiple of $6$ for every $n$”… But where do these problems come from? And have you ever stopped to think how magical this is? If I gave you some random polynomial in $n$ and asked you if it always output multiples of $6$, the answer would almost always be “no”! So if you really needed to come up with an example of this phenomenon, how would you do it? In this blog post, we give one approach!
I want to give some sort of attribution for this, since I remember reading about this exact topic… like a long time ago. Maybe 6 or 7 years ago? I’m sure that I saved the relevant article1 in my zotero, but I can’t find it for the life of me! Regardless, I want to emphasize that the whole idea for this topic (using Pólya-Redfield counting to build these divisibility problems) is not mine.
I’ve wanted to write a post on Pólya-Redfield counting for years now, since it was a pet topic of mine as an undergrad, but I think I was always planning too big a scope. This is a very bite-sized problem, and I won’t go into the theory very deeply, so I think it should make for a blog post I can finish in a day2.
Let’s get to it!
Ok, first, how might we come up with problems like this? We want a polynomial $P(n)$ and an integer $k$ so that $P(n)$ is always a multiple of $k$. That is, so that $P(n) / k$ is always an integer!
But what are sources of integers? If we put our combinatorial hats on, we learn that we had better be counting something! That’s the quickest way to ensure that we get an integer answer at the end of the day. So we want a polynomial so that as we vary $n$, the value $P(n) / k$ counts… something.
At this point, you might be inspired by The Lemma Which is Not Burnside’s, which says that when a group $G$ acts on a set $X$, the number of orbits is
\[\left | X \big / G \right | = \frac{1}{|G|} \sum_g |X^g|\]where \(X^g = \{ x \mid gx = x \}\) is the set of fixed points of $g$.
This is great, since in some sense it’s “where division comes from”. I don’t want to get into categorification here, but when we say we’re thinking of numbers as the cardinality of some set (to guarantee they’re integers) we’re really categorifying our problem. There’s been lots of work showing how various operations on numbers lift to categorified operations on the category of finite sets, and the only way I know of to categorify division is to take the orbits of some group action3. Hopefully this also serves to show that categorification doesn’t need to be scary! It can be incredibly simple, just thinking about finite sets and what we can do to them… Though maybe people who read my blog are already convinced of that, haha.
Regardless, this orbit-counting formula is close to what we want! It gives us access to division. So if we could only find a family of sets $X_n$, all of which admit a $G$-action, then maybe we could have $P(n) = \sum_g |X_n^g|$ and thus $P(n)$ will always be divisible by $|G|$, since $P(n)/|G|$ counts the orbits $|X_n \big / G|$!
This is exactly what Pólya-Redfield counting buys us! I really want to write a blog post with lots of pretty pictures that explains this in detail, but maybe just for today I’ll allow myself to be a bit less thorough. If you want to see this motivated with pretty pictures, I’ll point you to some slides by my undergrad advisor Klaus Sutner4. These are from the 2023 version of the class where I first met him back in… 2017? It’s better to not think about that, haha.
Moving on, say we have a set $X$ with a $G$-action. Then we think about all the ways to “color” $X$ with $n$-many colors. Precisely these are functions from \(X \to [n]\), and they pick up a natural $g$ action by sending the function $f : X \to [n]$ to the function $(gf)(x) = f(g^{-1}x)$5. These function spaces6 \((X \to [n])\) will be our sets $X_n$, and all that’s left is to see how to compute $|X_n \big / G|$, ideally in a way that’s uniform in $n$. Now (a corollary of) the main Pólya-Redfield theorem says:
where $c(g)$ is the “cycle count” of $g$. We can view the action of $G$ on $X$ as a homomorphism $\alpha$ from $G$ to the symmetric group $\mathfrak{S}_X$. Then $\alpha(g) \in \mathfrak{S}_X$ is a permutation, so decomposes into a product of cycles. The number $c(g)$ is perhaps the dumbest invariant you can think of: just count the number of cycles!
This is exactly what we want, since it tells us that the polynomial $P(n) = \sum_g n^{c(g)}$ is always divisible by $|G|$, since the quotient is exactly counting the orbits of the action of $G$ on \((X \to [n])\)!
Again, unfortunately I’ll leave the derivation of this formula (and the many many other useful things the Pólya-Redfield theory buys you) for another day, but at least we can do some quick examples!
First, say we want to count the number of bracelets you can make with $6$ beads, provided you have $n$ many types of beads available. Obviously if you were looking at bracelets in the real world that you can move around, the following two bracelets are actually the same:
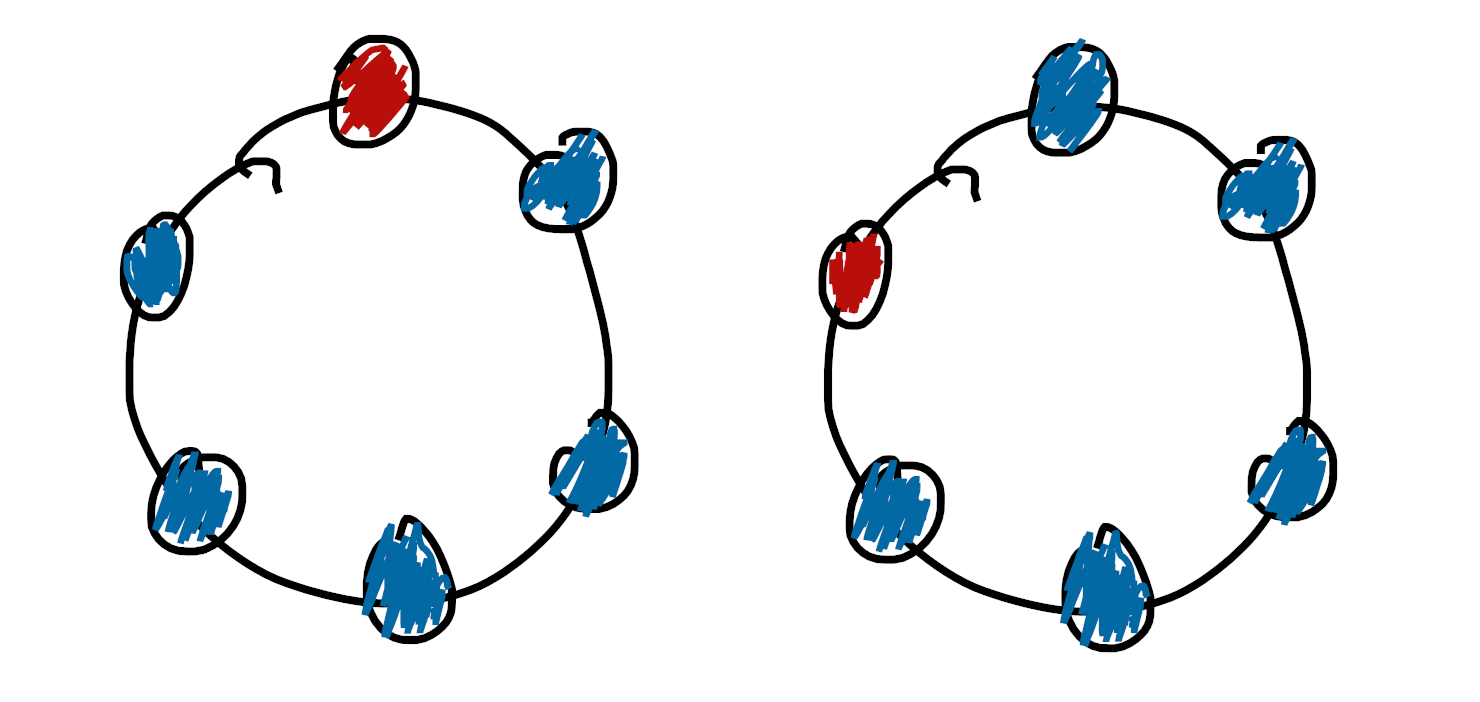
so we want to count the number of ways to color this picture with $n$ colors (this is a choice of bead in each position), but only up to the obvious $\mathbb{Z} / 6$ action on the space of colorings7!
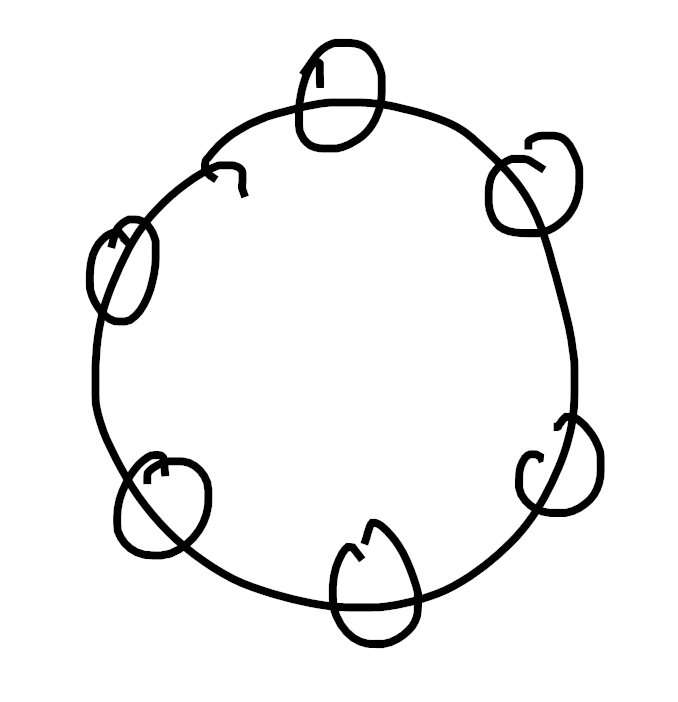
Now choose an isomorphism between the colorable places of our configuration and the standard set of size $6$, for instance, this is likely to be a common choice:
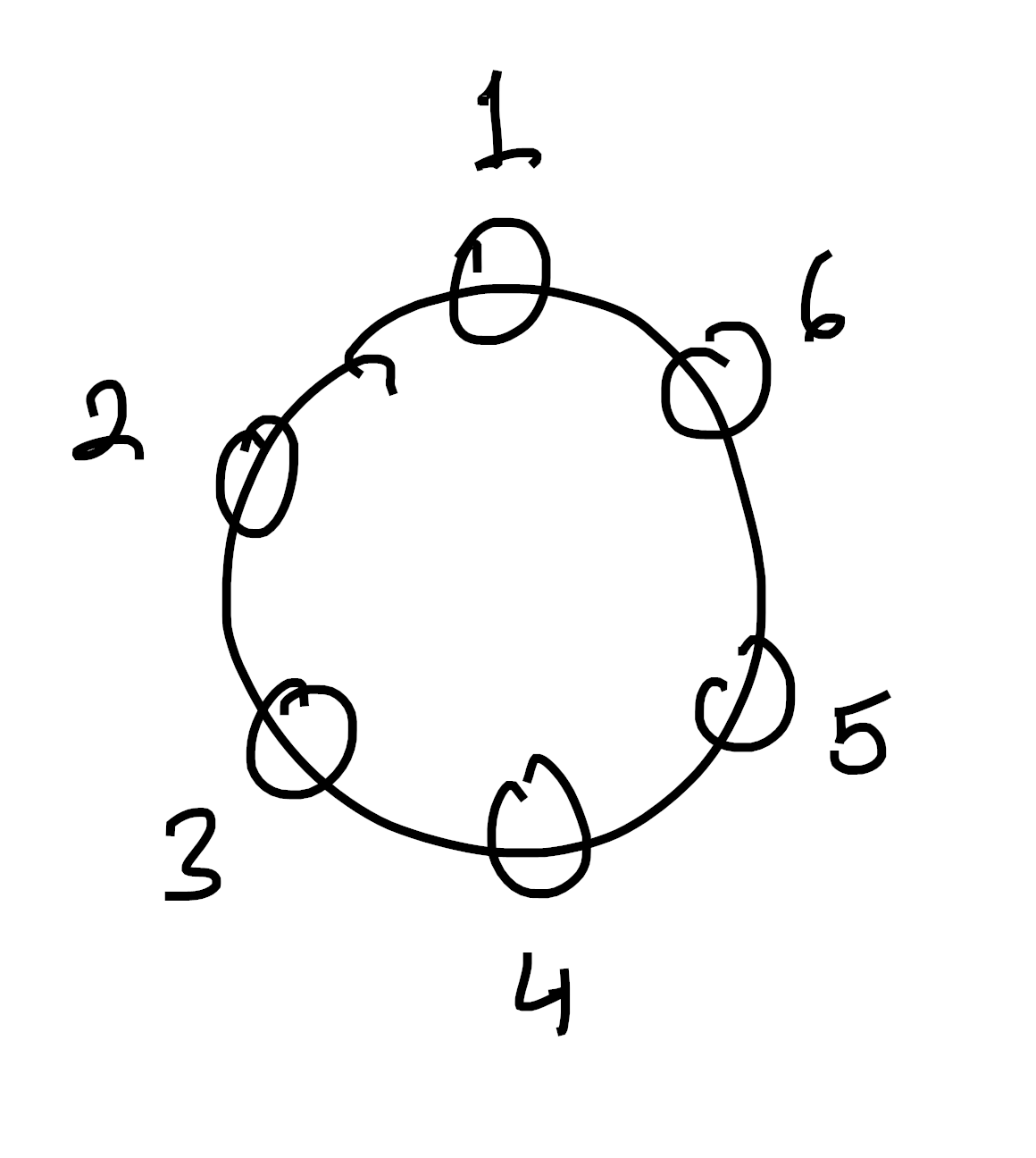
After making this identification our action is a map $\mathbb{Z}/6 \to \mathfrak{S}_6$, and thus we can compute cycle decompositions as follows:
| Element $g \in \mathbb{Z}/6$ | Image in $\mathfrak{S}_6$ | Number of Cycles, $c(g)$ |
| $0$ | $(1)(2)(3)(4)(5)(6)$ | $6$ |
| $1$ | $(1 \ 2 \ 3 \ 4 \ 5 \ 6)$ | $1$ |
| $2$ | $(1 \ 3 \ 5)(2 \ 4 \ 6)$ | $2$ |
| $3$ | $(1 \ 4)(2 \ 5)(3 \ 6)$ | $3$ |
| $4$ | $(1 \ 5 \ 3)(2 \ 6 \ 4)$ | $2$ |
| $5$ | $(1 \ 6 \ 5 \ 4 \ 3 \ 2)$ | $1$ |
Using this, we see that the number of bracelets with $n$ beads, up to our $\mathbb{Z}/6$ action is
\[\frac{1}{|G|} \sum_g n^{c(g)} = \frac{1}{6} \left ( n^6 + n^1 + n^2 + n^3 + n^2 + n^1 \right ) = \frac{1}{6} \left ( n^6 + n^3 + 2n^2 + 2n \right )\]Since this is counting the number of orbits, it must be an integer, and so for every $n$, the polynomial $P(n) = n^6 + n^3 + 2n^2 + 2n$ has to be divisible by $6$, as promised!
Let’s see a harder one, which (in the interest of speed) I stole from Klaus’s lectures:
How many ways can you fill a tic-tac-toe board with $X$s and $O$s, up to rotation and reflection?
We have configurations like the following (I’ve already chosen a bijection between our colorable places and the standard set with $9$ elements):
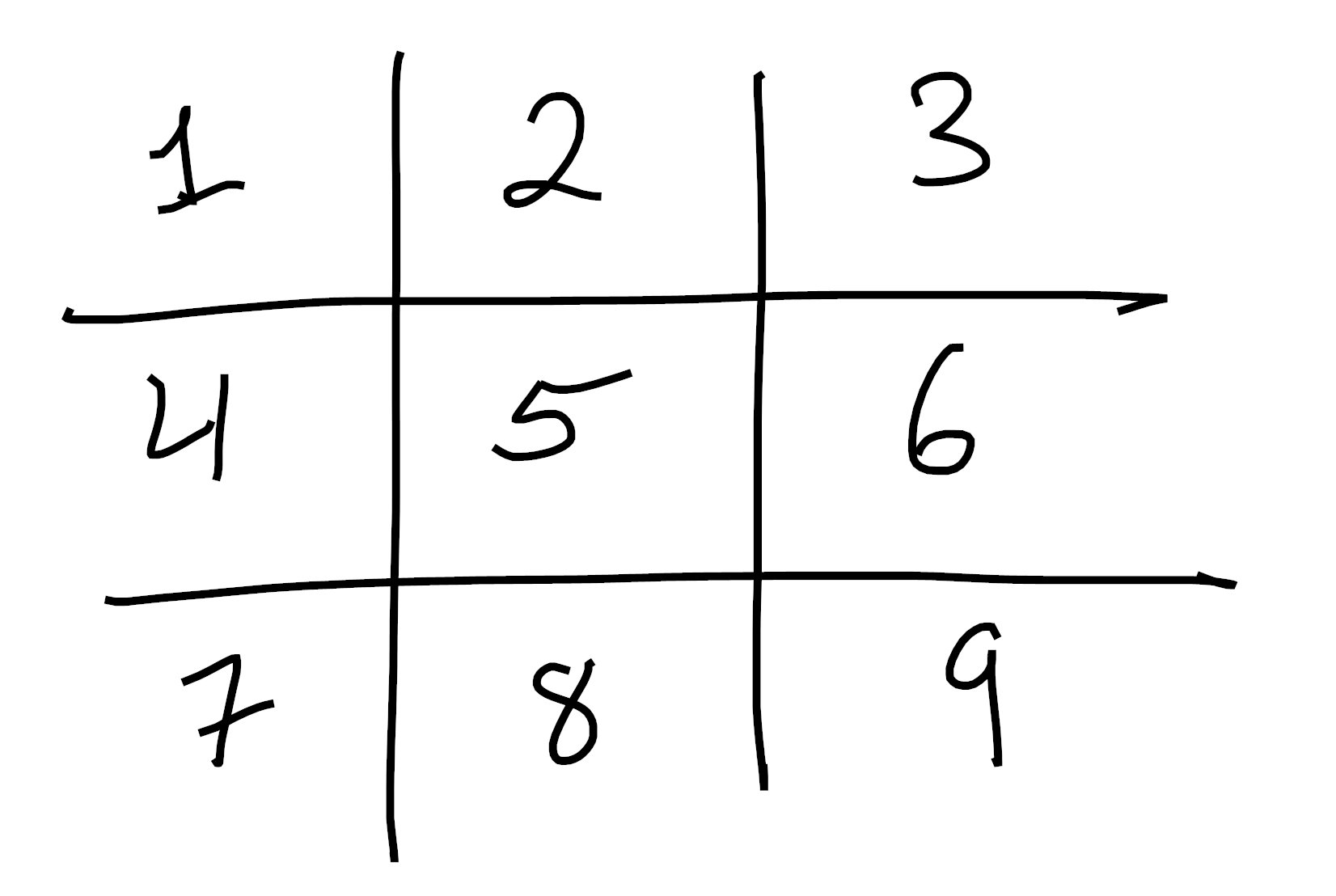
Now we want to color each slot $X$ or $O$, and quotient out the action of the dihedral group in order to view the following colorings as “the same” (of course, these aren’t the whole orbit! There’s many other rotations and reflections which are also equivalent):
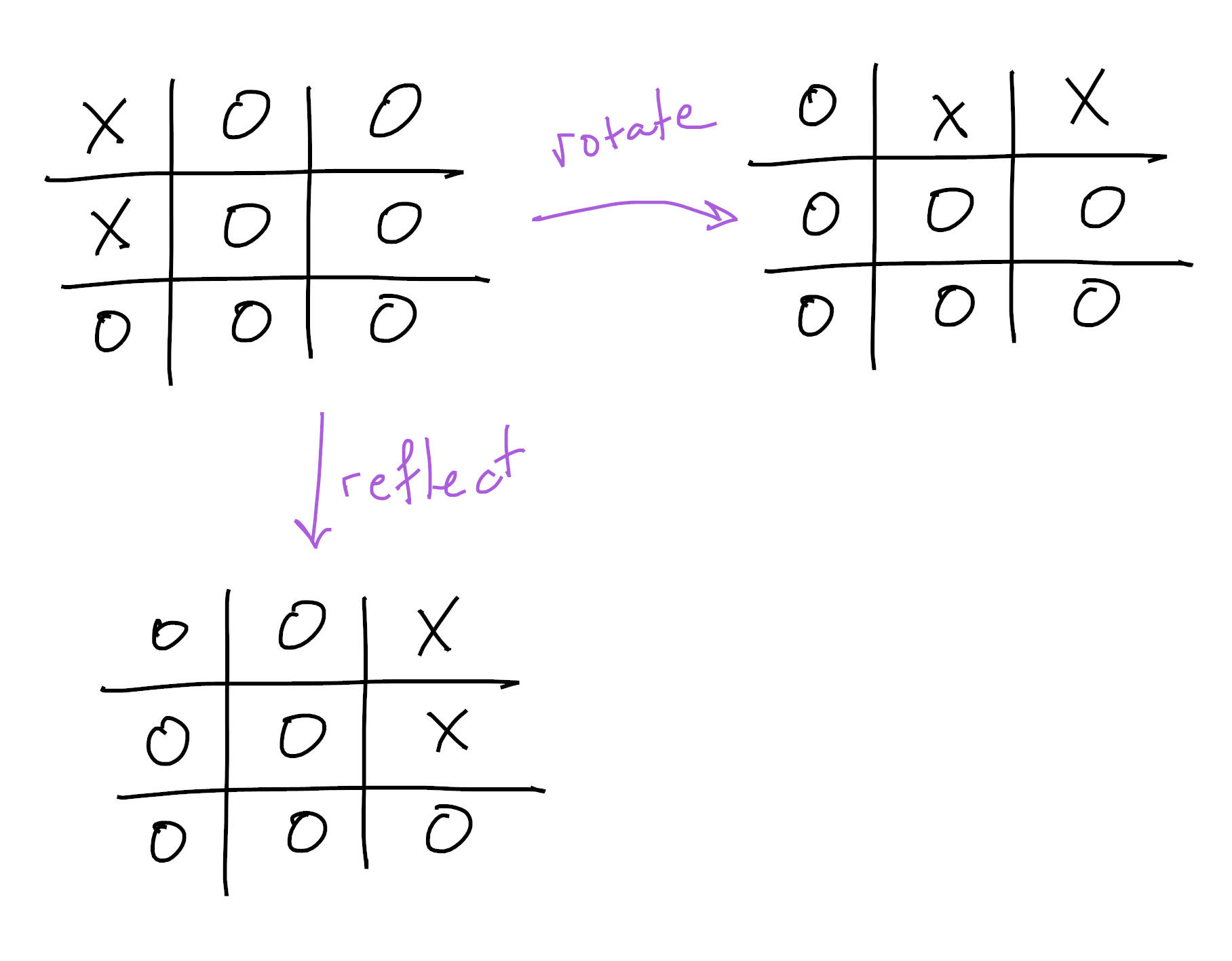
Notice we’re also not worried about which colorings come from actual games of tic-tac-toe!
How does Pólya-Redfield tell us to proceed? Well, the dihedral group $D_{2 \cdot 4}$ has $8$ elements, built out of rotations and reflections. Say that $r$ is the clockwise rotation shown above, and $s$ is the horizontal flip shown above. Then using the numbering system from before, we compute
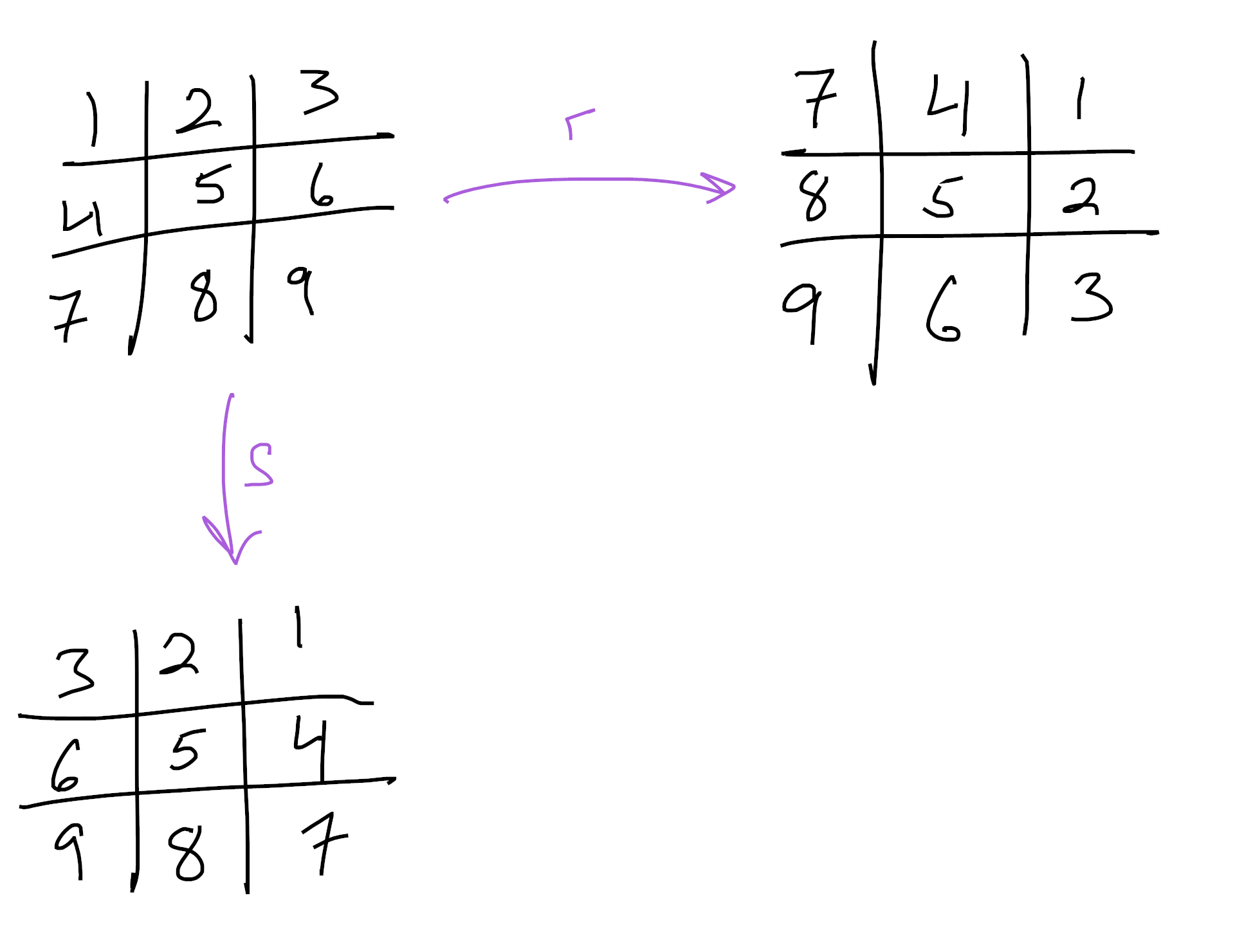
so that, in cycle notation:
\[r \mapsto (1 \ 7 \ 9 \ 3) (2 \ 4 \ 8 \ 6)(5)\] \[s \mapsto (1 \ 3)(4 \ 6)(7 \ 9)(2)(5)(8)\]Since $r$ and $s$ generate the whole dihedral group, we’re done with the hard work! Now a computer algebra system like sage can compute the rest of the table from these by multiplying them together:
xxxxxxxxxx# Build a permutation group generated by r and s as abover = '(1,7,9,3)(2,4,8,6)(5)'s = '(1,3)(4,6)(7,9)(2)(5)(8)'G = PermutationGroup([r,s])# print the cycle decomposition of every element of Gfor g in G: print(g.cycle_string(singletons=True))As a cute exercise for those new to group theory, try computing these 8 permutations yourself! Can you figure out which one comes from which element of the dihedral group? Can you see how they relate to the usual presentation $G = \langle r, s \mid r^4, s^2, srs=r^{-1} \rangle$?
From here it’s easy to read off the polynomial! If we have $n$-many available colors to put in each slot of the tic-tac-toe board, then the number of possible boards, counted up to rotation and reflection is given by
\[\begin{align} \left | (\mathtt{TicTacToeBoard} \to [n]) \big / G \right | &= \frac{1}{|G|} \sum_g n^{c(g)} \\ &= \frac{1}{8} \left ( n^9 + 4n^6 + n^5 + 2n^3 \right ) \end{align}\]Since we’re trying to color the board with only two colors, $X$ and $O$, we see the number of ways is
\[\frac{1}{8} \left ( 2^9 + 4 \cdot 2^6 + 2^5 + 2 \cdot 2^3 \right ) = 102\]Now we’ve really made two predictions here. First, that $P(n) = n^9 + 4n^6 + n^5 + 2n^3$ will be a multiple of $8$ for whichever $n$ you plug in. Second, that this quotient really is counting the tic-tac-toe boards! Let’s take a quick second and ask sage how true those look.
First, we can just plug in a few thousand $n$s and see if we ever hit anything other than a multiple of $8$:
xxxxxxxxxxfoundException = Falsefor n in range(1,10000): p = n^9 + 4*n^6 + n^5 + 2*n^3 if (p % 8) != 0: foundException = True print("uh oh! P({0}) is not a multiple of 8!".format(n)) breakif not foundException: print("^_^")Second, we know there’s only $2^9 = 512$ many ways to 2-color a tic-tac-toe board without counting rotations and reflections. So it’s not too time consuming to just list all of them and remove any we’ve seen before!
xxxxxxxxxxfrom itertools import productcolors = [0,1]boards = (((a,b,c), \ (d,e,f), \ (g,h,i)) \ for (a,b,c,d,e,f,g,h,i) in \ product(colors,repeat=9))def rotate(b): ((a,b,c), \ (d,e,f), \ (g,h,i)) = b return ((g,d,a), \ (h,e,b), \ (i,f,c)) def reflect(b): ((a,b,c), \ (d,e,f), \ (g,h,i)) = b return ((c,b,a), \ (f,e,d), \ (i,h,g))# this is actually kind of stupid, and computes # the orbit with duplicates... But that's fine # for numbers this small.def orbit(b): return [b, \ rotate(b), \ rotate(rotate(b)), \ rotate(rotate(rotate(b))), \ reflect(b), \ rotate(reflect(b)), \ rotate(rotate(reflect(b))), \ rotate(rotate(rotate(reflect(b))))] seen = []for b in boards: if set(seen).isdisjoint(orbit(b)): seen.append(b)print(len(seen))So there we go! This actually ended up taking two days to write, since yesterday I got distracted from my distraction when I was talking to a friend about connections and how curvature is related to force in physics. I realized I don’t actually understand that as well as I thought I did, so I had to spend some time rereading a bunch of physics stuff, which was super fun, even if it took a while, haha.
If you’re ever on a deserted island and you find yourself needing polynomials whose outputs are always divisible by some fixed number, this is an endless source! You might ask if every such polynomial arises from Pólya-Redfield counting in this way, and that’s obviously false (since, for instance, we’ll never get any constant terms)… But it’s not obviously false that every such polynomial arises from Pólya-Redfield counting after a change of variables! So with no intuition at all for whether it’s true or false, let me pose that as a conjecture:
Conjecture:
If $p$ is a polynomial so that $p(n)$ is a multiple of $k$ for every $n$, then there is a set $X$ and a group $G$ of order $k$ and a polynomial $f$ sending integers to integers so that
\[\frac{1}{k}p(n) \text{ counts the orbits } |(X \to [f(n)]) \big / G|\]Maybe $f$ can even be taken to be of the form $an+b$, why not. I haven’t thought about it either way, haha.
For anyone interested in thinking about this conjecture, it’ll be nice to know that every polynomial sending integers to integers is an integer linear combination of binomial coefficients (see here). Amusingly, this was also shown by Pólya!
You can push this further (as mentioned in the same wikipedia article) to note that $k \mid p(n)$ for all $n$ if and only if in the above representation $p = \sum c_i \binom{x}{i}$, all the $c_i$s are multiples of $k$. So we have an extremely concrete classification of these polynomials, which one might use to (dis)prove the conjecture8!
As a cute aside, we’ve actually talked about this basis for polynomials in terms of binomial coefficients before! Seeing them turn up here was like seeing an old friend.
Thanks again for hanging out, all! This was super fun, and it was a nice diversion from the blog post about my thesis work. It’s loooong, but really interesting, and I think people will enjoy it. This stuff relating fukaya categories, topological field theories, and representation theory is some of the coolest math I’ve ever seen, and I couldn’t have asked for a more fun thesis topic.
Of course, I also need to get the topological topos posts cleaned up and submitted to journals, and I have a fun project that I want to finish up which will be interesting to categorical logicians and algebraic geometers! (At least, algebraic geometers of a certain kind, haha). There’s always more to do, but that’s part of the fun of it! After two months applying to postdocs and barely doing any math at all, I’m thrilled to be back at it ^_^.
Alright, stay safe, all! We’ll talk soon 💖
-
or maybe it was a blog post or an mse question or something… Or maybe a footnote in a published paper? Part of why I can’t find it is because I don’t remember anything about where I read it! And back when I was an undergrad I was much worse about leaving myself searchable notes so I can quickly find interesting things again. ↩
-
If you’re curious why I decided to make this blog post now, I just started learning about cluster algebras today, and in the first lecture of Pavel Galashin’s series on the subject he mentions a recurrence relation which magically always gives integers, despite division happening. This reminded me of these polynomials which always give outputs divisible by some number (which is an easier version of the same phenomenon), and I went looking for the original article to share on mastodon. I couldn’t find it, so… I guess I’m writing one!
John Baez and Jim Dolan and I also talked about species and structure types in our last meeting, and so I think I was also somewhat primed to think about generating functions and Pólya-Redfield counting based on that conversation. ↩
-
You need groupoids and “groupoid cardinality” to have access to division in general, since this lets you get rational numbers (and even certain real numbers!) as cardinalities. See, for instance, John and Jim’s famous paper From Finite Sets to Feynman Diagrams or this MO post for more. ↩
-
I saved a copy of these slides local to this blog to make sure they’re always available, but if you want them right from the horse’s mouth you can find them here, and a course schedule with all the available lecture slides here. ↩
-
As long as I’m missing my undergrad years, I’ll pass on an insight from one of my favorite undergrad professors Clinton Conley about this seemingly weird $g^{-1}$:
Remember when you were learning how to graph functions and if you want to move the graph of $f(x)$ to the right by $c$, you look at the function $f(x-c)$? This trips up a lot of students first learning things, since it seems backwards to subtract $c$ to move to the right, especially since moving up and down has the much more sane behavior that $f(x)+c$ moves you up by $c$ units!
This is the same phenomenon, where the action on the input is contravariant (and we act on $x$ by the inverse of $c$) while the action on the output is covariant (and we act on $f(x)$ by $c$)!
There’s also something to be said here about left vs right actions, but I won’t say it, haha. Hopefully this Clinton-ism helps this make more sense, since I remember it really helped me when I was younger! ↩
-
I guess my type theory background is showing in this notation, haha. ↩
-
I think when most people talk about these bracelet problems, they quotient by the dihedral group instead of the cyclic group. This is because you can flip a bracelet over in 3D, so you have access to reflections too. I’m ignoring that for the sake of the example, though, and just counting things up to rotation. ↩
-
This is also a much more efficient source of polynomials for undergrad divisibility problems, but it wouldn’t have been anywhere near as fun! ↩