Life in Johnstone's Topological Topos 1 -- Fundamentals
03 Jul 2024 - Tags: life-in-the-topological-topos , featured , topos-theory
I’ve been thinking a lot about the internal logic of topoi again, and I
want to have more examples of topoi that I understand well enough to
externalize some statements. There’s more to life than just a localic
In particular, it would be nice to throw some gros topoi into the mix, and where better to start than Johnstone’s topological topos? This topos is fairly small (which makes explicit computation easy) and is very well studied (which makes finding references and examples merely annoying instead of totally impossible). Eventually I’ll want to learn about the effective topos1 (and other realizability topoi more generally), various smooth topoi, etc. but let’s take them on one-at-a-time!
The topological topos
Well, if we’re working in
Then if you want to work with spaces, you have to constantly keep track of
what topology you’re working with. For example, there’s lots of topologies
you can put on
Nowadays the “right” topology is usually “obvious2”, but this is only because we’re able to stand on the shoulders of countless 20th century mathematicians! I think most people would be hard-pressed to come up with, say, the compact-open topology if they hadn’t seen it before!
Of course, carrying around this ~bonus structure~ becomes most pronounced
when working with continuous maps! Now, instead of just defining a function
and moving on with your life, we’re constantly burdened to check that our
function
Thankfully there’s a better way!
Every set in

This is great for a couple reasons. First, say you build a type
Second, by the same logic, any theorem we’re able to prove constructively
is automatically true in
In the process of learning about
Let’s get started!
What Is
First, what even is the topological topos? It’s sheaves on some site, of course, but which one?
Write
Then let’s look at the full subcategory of
We’ll say more about this definition in a
minute, but first let’s see how we can picture objects of
A presheaf on this site is a pair of sets
- There’s a map
- There’s a unique map
- For every continuous function
You should think of elements of
The unique map
The sheaf condition for the canonical topology guarantees that
if every subsequence of
Can you prove that this is reasonable?
If
You might find it helpful to case on whether
As a cute exercise can you find a simple description of the
arrows in
solution
A natural transformation betweenNow every topological space
If we restrict attention to the full subcategory of sequential spaces,
then
Importantly, you should think of this is a super mild condition, since lots of natural spaces of interest are sequential. Just to name a few:
- all metric spaces
- more generally, all first countable spaces
- every CW-complex
- every noetherian ring spectrum
This tells us that a huge subcategory of topological spaces embeds fully
faithfully into
There’s another definition of
Having
With this in mind, some authors define
This gives a different informal justification for the close connection between
So, with this smaller site in hand, one way to think about objects in
But how do we know that these two definitions agree? I wasn’t able to find this written down anywhere, but it’s easy to check for ourselves!
The key observation is that
Since
In particular, the two common definitions really do give equivalent topoi!
So, finally, what is the Canonical Topology?
For the site with two objects,
If
A family
- It contains every constant map
- For every infinite
In particular, if a family contains every constant map
So, roughly, to prove that something “merely exists” in
If we want to use the site with one object
- every constant map
- For each infinite
This, unsurprisingly, doesn’t make too much difference. But note that
the site with two objects is obviously local in the sense of
The Elephant (C3.6.3(d)). So we learn that the global sections functor

In the original paper, Johnstone moreoever shows that the essential point
How Does
Here’s the tl;dr for this section, for ease of reference.
We have a sequence of fully-faithful embeddings of bicartesian closed categories, each of which admits a left adjoint, as shown below:

The embeddings preserve all limits (as right adjoints) but moreover preserve
the cartesian closed structure, as well
as certain “nice” colimits (in particular, all colimits involved in the
creation of CW-complexes). The exact definition of “nice” here is
explained in Johnstone’s original paper, but includes the coproduct. Additionally, the
image of a map
The left adjoints preserve all colimits, and moreover preserve finite products (and thus, in particular, models of algebraic theories).
Lastly, in case we restrict to the full subcategory of
“sequentially hausdorff spaces”, in the sense that every convergent sequence
has a unique limit, then the adjunction
Here
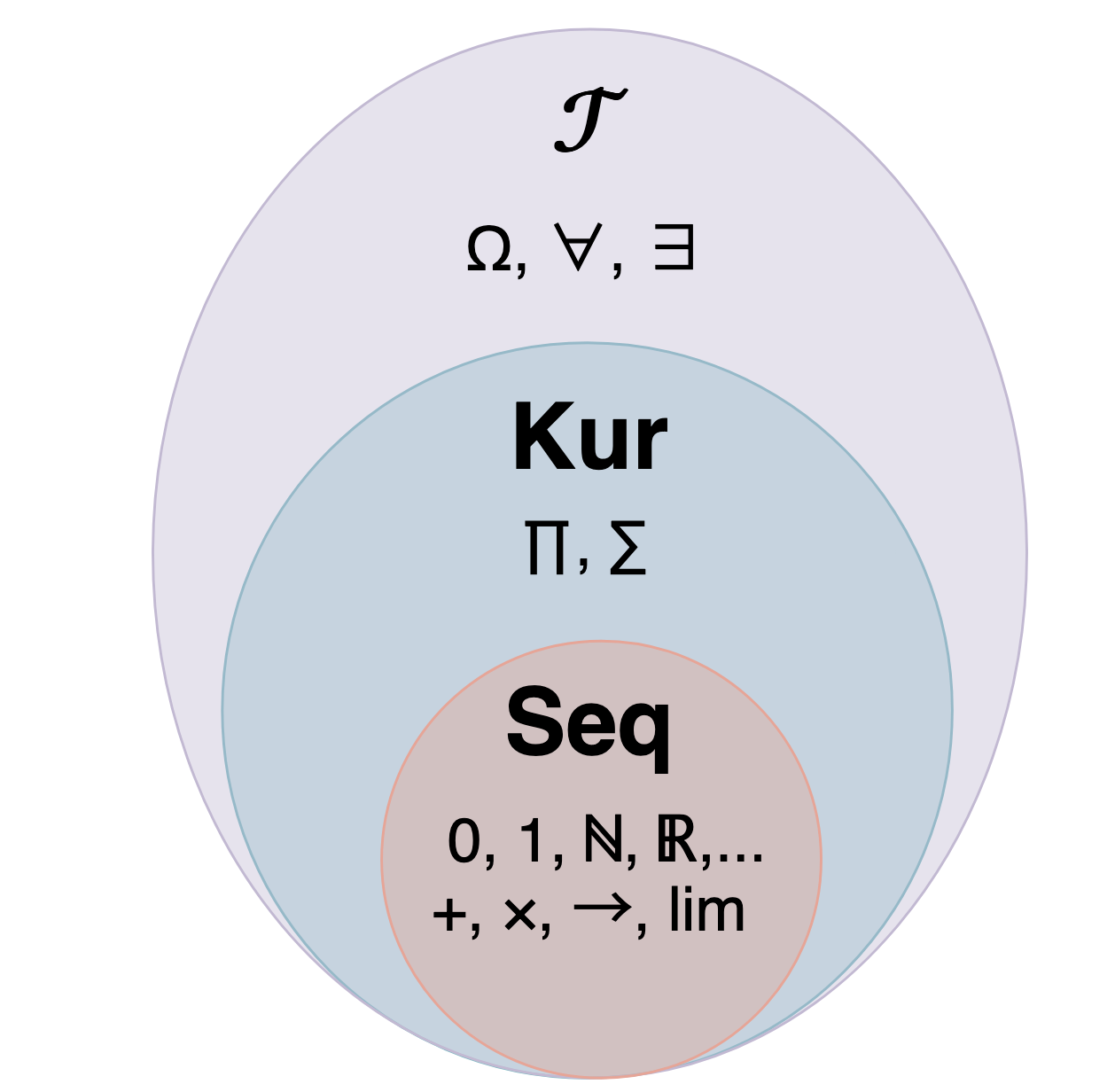
Colimits in
The relationship of limits in
If your spaces are locally compact, then the (finite)
product in
That’s a lot, so let’s go more in depth into what all of this means, haha.
We’ll start with the definition of a Kuratowski Limit Space (also called a subsequential space):
A Kuratowski Limit Space is a set
- For every
- If
- If, for some
We moreover call
- If
A function
Every sequential topological space is automatically a limit space, where we
just let the convergent sequences be the (topologically) convergent sequences.
Moreover, there’s a fully faithful embedding of limit spaces into
As a (not so tricky) exercise, you might want to verify that this
map from
This basically amounts to comparing axiom (3) for limit spaces to
the definition of a cover of
Taken together, we have fully faithful embeddings
In fact, Johnstone’s original paper shows that
Concretely, this left adjoint takes an object of
Moreover, the embedding
We say a subset
Also, notice that this reflection possibly adds new convergent sequences.
Maybe our limit space
Conversely, the subobjects of a space
In general, we can think of objects in
But this intuitive picture tells us how to get an honest space from your
favorite object
The fact that the reflectors preserve finite products tells us that the
Lastly, the cartesian closed structure on
From this information, there’s a few simple corollaries that I want to
mention explicitly, since they give more relationships between
First, fully faithful functors reflect isomorphisms, so if we can prove
in
Similarly, if
Dually, if
This is great and all, but the only way to really get some intuition for
how computations in
This is the discrete space with two points
We think of
This tells us immediately that
We can instead see this by thinking of
As a last aside, it’s not hard to see that
This is the sierpinski space, which also has two points
We think of
A similar yoneda argument shows that
As a cute aside, this tells us that
This is the “co-sierpinski space”. It has two points
Unsurprisingly, this is the space of Closed Propositions,
and maps into
At this point you know what’s going on. This space has two points,
This interpretation also makes it more believable that it should correspond
to
Notice that this is again a complete lattice. We can see this either
because
This is the subobject classifier, or the space of all propositions!
Maps
Notice that, for
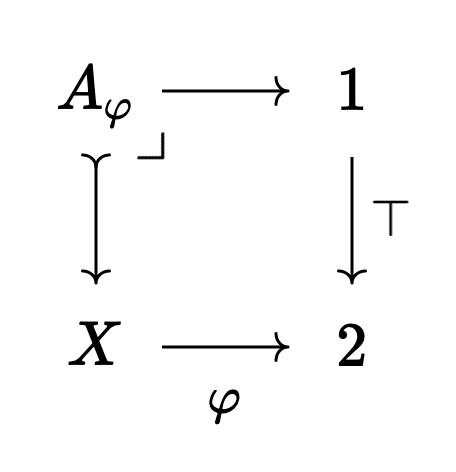
exists in
Note that this
Now, what does the space of all propositions look like in
Johnstone shows that
- there’s exactly one proof that
- there’s one proof that
Here a “closed ideal of subsets of
In the above,
- if
- if every infinite subset of
These correspond, basically, to axioms (2) and (3) for limit spaces. This will make sense once we understand how this subobject classifier actually classifies subobjects!
Say that we have a subobject
On points, we have
Well, to what extent is
If
We’ll let
This shows where these conditions on “closed ideals of subsets” come from!
If
For example, say
Lastly, note that if we reflect
There’s an object
It turns out that in
We won’t show this here because we’ll show something more general in just a few bullets!
Since
Now, in the realm of classical topology, since
Again, one can also ask about the points of the locale object
“cantor space”. And again, we find that the points of this locale
are represented by
For each
So “
So this space, externally, is the closed subspace of cantor space corresponding
to the decreasing binary sequences. This space is homeomorphic to
Regular Locales
Let
In particular, if
In particular again, the dedekind reals object is
Putting these facts together (in the special case of
We know that
Now let’s look at
where
Then if
But it’s not hard to see the only elements in
So where did we start, and where did we end? We see that
Note that in this proof regularity was only used to check that the
convergent sequences in
This result tells us that coherent locales (as defined in
Is there a flaw in this proof? Maybe we get out of this problem if the
prime ideal theorem in
I would be SUPER grateful if some experts chimed in! Feel free to leave a comment on this post, email me, or say something on mastodon.
How does
Like we said in the introduction, the topological topos
For instance some authors13 say that “a” topological topos is a category
of sheaves on a subcategory
It’s natural to ask for a similar relationship between
Johnstone decides to not say anything more about the geometric morphisms
⚠ From this discussion, though, we learn that “the” topological topos
Characterizing “Honest Spaces” Internally
We saw earlier how every type we construct represents some space by
interpreting that type in
From this point of view it’s natural to ask when a type we’ve constructed
is already a space, without needing to do any reflection. Is there a
way to internally characterize the “honest spaces” amongst all the objects
in
The first step in this process is to recognize
This is implicit in Propositions 3.6 and 4.3 of Johnstone’s original paper.
Then, we use the fact that the full subcategory of sequentially hausdorff sequential spaces is equivalent to the full subcategory of sequentially hausdorff limit spaces! With this in mind, we define
and it’s easy to show that
In particular, this means that we can show an object of
Ok! That’s plenty for this post, where we’ve learned a lot of fundamentals
about what
Next up we’ll talk about topological algebras, and learn how
we can use the topological topos to reason smoothly about these things.
This is a shorter palate cleanser between this post (which is quite long)
and the third post on ~bonus axioms~ validated by
Thanks for hanging in there, and for all the encouragement while I was writing this! It’s been really exciting to know how many people are interested in reading this series ^_^.
As a last request, I’ll be turning this series into a paper in the very near future. If you have any suggestions for other examples to add, or axioms to check, or if you notice any typos or outright mistakes, definitely let me know! Also, experts, if you have any additional context you think would fit well in what’s shaping up to be quite a long survey of the topological topos that you want to get into the literature, please let me know that too! It’ll be nice for future mathematicians to have this all in one place!
As always, thanks for reading all! Stay safe, and talk soon 💖
-
I spent some time a few years ago (Feb of 2022, according to my Zotero) thinking hard about the effective topos. I think I was going to write a blog post about it, but I never got around to it.
I think I should be able to remind myself what was going on, and in a perfect world I would understand it much better now that I know more things, so hopefully I’ll finally write that post. This is particularly relevant now that Andrej Bauer and James Hanson have posted their preprint constructing a realizability topos where the reals are countable. ↩
-
And even then, it might not be obvious when you’re learning! I remember when I first learned pointset topology the idea of a “cylinder set” and the product topology made no sense to me! Honestly without the framework of topological categories or something similar, I could see people still being surprised that the box topology isn’t the “right” topology on an infinite product space! See, for instance, this old and highly upvoted mse question. ↩
-
After my last post on a constructive extreme value theorem, I wanted to see how it externalizes in topoi other than
I still haven’t totally figured out this story (though I’m much less weirded out by the idea since I remembered that scott topologies exist as a natural topology on the frame of opens), so I won’t say anything more in this post, but trying to understand
-
If you want a super concrete description, it’s equivalent to
with the subspace topology. ↩
-
Note that it’s entirely possible for two different elements
Indeed, this will be crucial later, for instance in our discussion of the subobject classifier
-
This is spelled out quite clearly in Johnstone’s original paper On a Topological Topos. Indeed, Johnstone computes the covering sieves very explicitly, and I highly recommend reading about it there. Of course, I’ll say a few words about it in this post too! ↩
-
It’s not immediately obvious that this presheaf is actually a sheaf, but it turns out to be. This is a nice exercise. ↩
-
But we must remember that products in
A sequence of pairs
-
If you want to understand how to compute (co)limits in
Particularly helpful is the observation that
-
Thanks to Morgan Rogers for letting me know that monics actually agree in all cases, which simplies the exposition of this section quite a lot. ↩
-
Thanks to Graham Manuell for letting me know that there’s standard notation for this (which the post now uses) besides what’s shown in Johnstone’s “Stone Spaces”. ↩
-
First, say we have a proof
Now let’s look at the more complicated case of a proof
-
eg, Moerdijk and Reyes in their Smooth spaces versus continuous spaces in models for synthetic differential geometry ↩
-
You might ask if there’s a way to characterize the whole of
I suspect there’s a way to do this, by defining the sequentially open subsets of
But this sounds rather complicated, and I’m really looking to get this blog post done, haha. Especially since I still have to convert it into a paper! ↩