Life in Johnstone's Topological Topos 3 -- Bonus Axioms

03 Jul 2024 - Tags: life-in-the-topological-topos , topos-theory

In the first post of the series, we talked about what the topological topos is, and how we can think about its objects (and, importantly, how we can relate computations in the topos $\mathcal{T}$ to computations with topological spaces in “the real world”). In part two, we talked about algebraic structures, and how (for example) groups in $\mathcal{T}$ are related to topological groups.

In that post we alluded to the presence of ~bonus axioms~ that allow us to reason in $\mathcal{T}$ more freely than in many other topoi. For instance, we have access to a certain amount of choice. We also have access to a powerful principle saying that every function between metric spaces is $\delta$-$\epsilon$ continuous!

In this post we’ll spend some time talking about these bonus axioms, and proving that they’re true (since a lot of these facts are basically folklore).

Let’s get to it!

---

First, let’s take a second to recall the definition of the grothendieck topology $J$ for $\mathcal{T}$. We’re going to be externalizing a lot of theorems, and it’ll be good to have the open cover condition on hand. Here’s what we wrote back in the first post, but you can of course read more in Section 3 of Johnstone’s original paper.

For the site with two objects, \(\{1, \mathbb{N}_\infty\}\), every (nonempty) family of arrows \(\{X_\alpha \to 1 \}\) is covering. So the interesting question is what a covering family of \(\mathbb{N}_\infty\) looks like.

If $S$ is an infinite subset of $\mathbb{N}$, we write $f_S$ for the unique monotone map \(\mathbb{N}_\infty \to \mathbb{N}_\infty\) whose image is \(S \cup \{ \infty \}\).

A family \(\{X_\alpha \to \mathbb{N}_\infty\}\) is covering if and only if both

1. It contains every constant map \(1 \to \mathbb{N}_\infty\)
2. For every infinite $T \subseteq \mathbb{N}$, there is a further infinite subset $S \subseteq T$ with \(f_S : \mathbb{N}_\infty \to \mathbb{N}_\infty\) in the family

In particular, if a family contains every constant map \(1 \to \mathbb{N}_\infty\) and a “tail of an infinite sequence” \(f_{\{x \geq N\}}\) for some $N$, then that family is covering.

So, roughly, to prove that something “merely exists” in $\mathcal{T}$, we have to provide a witness for every finite $n$, and these witnesses should converge to the witness for $\infty$.

If we want to use the site with one object \(\{ \mathbb{N}_\infty \}\), the condition is almost exactly the same. A family of maps is covering if and only if both

1. every constant map \(\mathbb{N}_\infty \to \mathbb{N}_\infty\) is in the family
2. For each infinite $T \subseteq \mathbb{N}$, there’s a further infinite $S \subseteq T$ so that $f_S$ is in the family.

This, unsurprisingly, doesn’t make too much difference.

---

Dependent Choice

To start, $\mathcal{T}$ models Dependent Choice. You can find a proof in Shulman and Simpson’s aptly named note Dependent Choice in Johnstone’s Topological Topos.

Say you have a relation $R \subseteq X \times X$ which is total in the sense that $\forall x . \exists y . R(x,y)$.

Then DC says for each $x_0 : X$, there’s a function $f : \mathbb{N} \to X$ so that $f(0) = x_0$ and for each $n$, $R(f(n), f(n+1))$.

This is intuitively obvious. After all, we start with $x_0$, then by totality the set \(\{ y \mid R(x_0,y) \}\) is inhabited. So we can choose an element $x_1$ from this set. Similarly we can choose an $x_2$ from \(\{y \mid R(x_1,y) \}\), and so on. Notice that the choices we make are allowed to depend on the choices that came before. After all, it’s possible that for two different choices \(x_1,x_1' \in \{ y \mid R(x_0,y) \}\) the sets \(\{ y \mid R(x_1,y) \}\) and \(\{ y \mid R(x_1',y) \}\) might be different, leading to different allowable choices of $x_2$!

Thus, DC basically tells us that recursive definitions work, even if we don’t have a canonical way to choose one of many options at each recursive stage. Indeed, most recursive definitions work by first choosing an $x_0$, and then arguing that the set of “allowable” next steps is always inhabited¹. For more information about DC and how to think about it, I recommend Karagila’s excellent paper on the subject.

Here’s an idiomatic example of dependent choice in action: The Baire Category Theorem for complete metric spaces.

The usual proof (say, from Karagila’s notes) doesn’t use LEM, so it goes through unchanged. We’ll present it here paying special attention to the use of DC.

$\ulcorner$ Let $V$ be open in $X$. We need to show that $V \cap \bigcap_n U_n$ is inhabited.

Since $U_1$ is strongly dense, we know that $V \cap U_1$ is inhabited, say by $x_1$. Now since $U_1 \cap V$ is open, we can find a radius $r_1$ so that

1. $0 \lt r_1 \lt 2^{-1}$
2. the (strongly closed) ball \(\overline{B(x_1,r_1)} = \{ y \mid d(x_1,y) \leq r_1 \}\) is contained in $V \cap U_1$

By dependent choice (and strong density of each $U_k$), we may recursively build a sequence of pairs $(x_n,r_n)$ so that

1. $0 \lt r_{n+1} \lt 2^{-(n+1)}$
2. the (strongly closed) ball $\overline{B(x_{n+1},r_{n+1})}$ is contained in $B(x_n,r_n) \cap U_{n+1}$.

By construction, then, the $x_n$s assemble into a cauchy sequence whose limit $x_\infty$ lies in each $B(x_n,r_n)$. Therefore $x_\infty \in \bigcap_n B(x_n,r_n) \subseteq V \cap \bigcap_n U_n$, so that $\bigcap_n U_n$ is dense, as desired. $\lrcorner$

Dependent Choice implies Countable Choice, which itself implies Weak Countable Choice. But WCC⁴ implies that the dedekind reals and the cauchy reals agree. And indeed one can show directly that in $\mathcal{T}$ both the dedekind and cauchy reals are given by $よ\mathbb{R}$.

Brouwer’s Principle

The next ~bonus axiom~ we’ll talk about is Brouwer’s Continuity Principle that “Every function $f : \mathbb{R} \to \mathbb{R}$ is continuous”!

Precisely⁵:

In fact, this is true for any (external) metric spaces $X$ and $Y$ where $X$ is (externally) locally compact! In particular, it’s also true that every function $\mathbb{N}^\mathbb{N} \to \mathbb{N}$ is $\epsilon$-$\delta$ continuous.

Note that it’s crucial here that we use the truncated $\exists$ rather than the untruncated $\Sigma$ in the statement of this theorem. Martín Escardó and Chuangjie Xu have shown that the untruncated version of this theorem isn’t just false in $\mathcal{T}$, it’s provably false in every topos!

Regardless, it’s shockingly hard to find this continuity principle written down anywhere, but it’s cited in lots of places! It’s definitely part of the folklore, and I’m happy to share a full proof! It’s a bit long, though, so I’m leaving it as an “appendix” at the bottom of this post. If you know of a reference, or of a slicker proof than the one I found, I would REALLY love to hear about it⁶!

Regardless, the truth of Brouwer’s principle tells us that $\mathcal{T}$ is a rather stronger version of Solovay’s Model. Solovay’s model validates \(\mathsf{LEM}+\mathsf{DC}+\)“every function $\mathbb{R} \to \mathbb{R}$ is measurable”.

In $\mathcal{T}$, we have $\mathsf{DC}$ and the stronger “every function $\mathbb{R} \to \mathbb{R}$ is continuous”. But the price we pay is LEM.

Omniscience Principles

We can ask about other nonconstructive principles too. For instance, Bishop’s Principles of Omniscience!

First, let’s look at the Limited Principle of Omniscience (LPO):

It’s clear from the last condition that LPO is false in $\mathcal{T}$. Since both \(\mathbb{N} + \{ \infty \}\) and \(\mathbb{N}_\infty\) are sequential, these internal types correspond to the expected spaces externally, where this is obviously not an isomorphism. After all, one space is discrete and the other isn’t.

That said, it can be hard to find example computations of people statements internal to a topos to statements in the real world, so just for fun let’s prove this again in a more complicated way:

$\ulcorner$ If it were true, then we would know $1 \Vdash \text{LPO}$. Now cashing out the universal quantifier, we would know that for every \(s \in 2^\mathbb{N}(\mathbb{N}_\infty)\)

\[\mathbb{N}_\infty \Vdash (\forall n . s_k(n) = 0_k) \lor (\exists n . s_k(n) = 1_k)\]

Here \(s_k : \mathbb{N}_\infty \to 2^\mathbb{N}\) is allowed to be any convergent sequence in cantor space, and we interpret $0_k$ and $1_k$ as constant sequences.

Let’s take $s_k$ to be the sequence $0^k 1^\omega$. That is, the $k$th element of this sequence, $s_k$, should be the point in cantor space with $k$ many $0$s followed by an infinite tail of $1$s. Note this sequence converges to $0^\omega$.

Now what would it mean to have $(\forall n . s(n) = 0) \lor (\exists n . s(n) = 1)$? We would have an open cover of \(\mathbb{N}_\infty\) where each element of that cover thinks that one of these disjuncts is true. But every covering seive of \(\mathbb{N}_\infty\) contains a function $f_U$ for $U$ an infinite subset of $\mathbb{N}$.

Now restricting $s$ to this member of the cover amounts to restricting $s$ to a subsequence, $s_{r_k}$.

Is it possible that \(\mathbb{N}_\infty \Vdash \forall n . s_{r_k}(n) = 0_{r_k}\)? This says for every convergent sequence \(n_k \in \mathbb{N}(\mathbb{N}_\infty)\), we must have \(s_{r_k}(n_k) = 0_{r_k}\) for all $k$. Of course, it’s easy to find a convergent sequence where this is false! We can just choose \(n_1 \gt r_1\) to make \(s_{r_1}(n_1) = 1 \neq 0\).

Is it possible for \(\mathbb{N}_\infty \Vdash \exists n . s_{r_k}(n) = 1_{r_k}\)? This says we can pass to a further subsequence \(s_{\ell_{r_k}}\) so that for some convergent sequence \(n_k \in \mathbb{N}(\mathbb{N}_\infty)\) we have \(s_{\ell_{r_k}}(n_k) = 1_k\) for all $k$. But of course this is false too! Every convergent sequence of naturals is eventually constant, say $n_k = N$ for $k \gg 1$. Then for $k$ large enough, we’ll have both $n_k = N$ and \(\ell_{r_k} \gt N\), in which case \(s_{\ell_{r_k}}(n_k) = 0 \neq 1\).

So we see that LPO externalizes to a false claim, and thus is not validated by $\mathcal{T}$. $\lrcorner$

Next, let’s look at the Lesser Limited Principle of Omniscience (LLPO):

This turns out to be true⁷! Just to show more ways to reason about the internal logic of topoi, we’ll prove this one by working with the category $\mathcal{T}$ directly. Since type theoretic functions externalize to arrows in $\mathcal{T}$, though, we’ll use type theory to label our arrows.

$\ulcorner$ Proposition 6.2 in Johnstone’s original paper implies that $\mathbb{R}$ is the pushout of the closed cover

Now showing $\forall x : \mathbb{R} . (x \geq 0) \lor (x \leq 0)$ amounts to building a section of the projection $\pi : \sum_{x : \mathbb{R}} \lVert (x \geq 0) + (x \leq 0) \rVert$. Here I’ve also cashed out the $\lor$ for a propositional truncation of a coproduct.

But by the universal property of the pushout, we get a map $s : \mathbb{R} \to \sum_{x : \mathbb{R}} \lVert (x \geq 0) + (x \leq 0) \rVert$ as below. Note the truncation \(\lVert (x \geq 0) + (x \leq 0) \rVert\) is crucial for making the middle square commute!

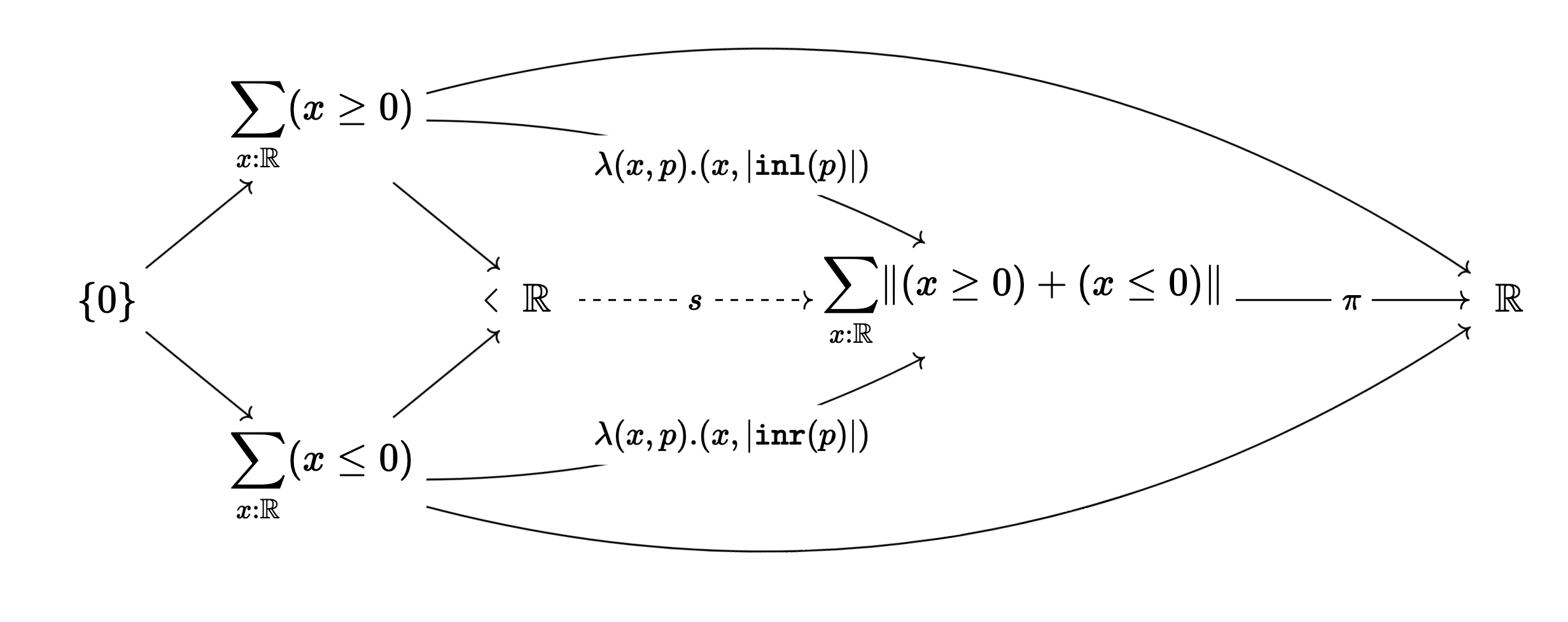
Moreover, since both $\pi s$ and $\text{id}_\mathbb{R}$ make the outer square commute, they must be equal by uniqueness in the universal property. So $s$ is the desired section of $\pi$, and $\mathcal{T}$ models LLPO. $\lrcorner$

Next on this list is Markov’s Principle (MP):

MP is true in $\mathcal{T}$, and this is not so hard to show. We’ll write this proof in a slightly more conversational style, but we encourage the reader interested in learning topos theory to check all the details with the forcing language.

$\ulcorner$ We want to show

\[1 \Vdash \forall s : 2^\mathbb{N} . (\lnot \forall n . s(n) = 0) \to (\exists n . s(n) = 1)\]

so we fix a convergent sequence \(s_k : \mathbb{N}_\infty \to 2^\mathbb{N}\). We want to show that if, for all \(f : \mathbb{N}_\infty \to \mathbb{N}_\infty\)

\[\mathbb{N}_\infty \not \Vdash \forall n . s_{fk}(n) = 0 \quad \quad (\star)\]

then we must have

\[\mathbb{N}_\infty \Vdash \exists n . s_k(n) = 1.\]

To show this existential claim, we need to provide a conergent sequence $n_k$ so that each $s_k(n_k) = 1$. But taking $f$ to be a constant function in $(\star)$, we learn that such an $n_k$ exists for each $k$. Moreover, since \(s_k \to s_\infty\), there is a $k \gg 1$ so that $s_k$ and $s_\infty$ agree on the first $n_\infty + 1$ many bits, so that we may take $n_k = n_\infty$ when $k$ is large enough. Thus the sequence converges, as desired. $\lrcorner$

Now WLPO is easy:

Now, it’s easy to see that MP + WLPO $\implies$ LPO (look at the analytic versions). So we learn indirectly that $\mathcal{T}$ cannot satisfy WLPO. Of course, here’s a more direct proof that the analytic version can’t work:

$\ulcorner$ Consider the sequence $x_n = \frac{1}{n}$, converging to $0$, as an element of \(\mathbb{R}(\mathbb{N}_\infty)\).

If $\mathcal{T}$ were to model WLPO, it would mean (among other things) that some subsequence of $x_n$ would be either everywhere $0$ or everywhere nonzero. But no subsequence has this property, since $x_n$ is nonzero for each finite $n$, but zero at $n=\infty$.

So $\mathcal{T}$ does not model WLPO. $\lrcorner$

As an aside, in all of these statements we’re using the “truncated” $\lor$ and $\exists$, and it’s natural to ask what happens if we change these to their “untruncated” versions $+$ and $\Sigma$.

It’s a theorem of Martín Escardó that

• truncated and untruncated LPO are equivalent
• truncated and untruncated WLPO are equivalent, and are equivalent to untruncated LLPO
• truncated LLPO is weaker than untruncated LLPO

In fact, in his agda files, Martín wonders if there’s a place in the literature where untruncated LLPO and WLPO are shown to be inequivalent.

He mentions that $\mathcal{T}$ should be an example, and here we’ve shown that in fact it is! After all, $\mathcal{T} \models \text{LLPO}$ but $\mathcal{T} \not \models \text{WLPO}$!

---

Bar and Fan Theorems

The Bar and Fan theorems are closely related to the nice properties of baire space and cantor space (respectively) as spaces rather than as locales. The locales are always well behaved, but in some topoi these locales fail to have enough points, so that the baire space and cantor space as sets of points may be lacking.

Since we showed in part 1 that spatial sequential regular locales always have enough points in $\mathcal{T}$, we see that baire space and cantor space both have enough points! By Propositions 3.12 and 3.13 in van den Berg and Moerdijk’s Derived rules for predicative set theory: An application of sheaves we see that the Monotone Bar Theorem and the Full Fan Theorem hold in $\mathcal{T}$.

This is also the best we can do. Since the Full Bar Theorem is known to imply LPO, and $\mathcal{T} \not \models \mathsf{LPO}$ we know that we can’t improve the monotone bar theorem to the full bar theorem in $\mathcal{T}$.

discussion of the ~bonus exercise~

The idea here is that a general subobject of a sequential space X is a subset of the points of X equipped with some topology making the inclusion continuous. A decidable subobject is a clopen subset of the points of $X$ equipped with the induced topology (do you see why?). Of course, since $2^{\lt \mathbb{N}}$ is discrete, it's not hard to see that _every_ subobject is decidable! This means in proving the theorem for decidable subobjects you've actually proven the theorem for _all_ subobjects!

---

De Morgan and LEM

Obviously LEM fails, since $\Omega \not \cong 1+1$. But what about De Morgan’s Laws?

It turns out that $\mathcal{T}$ is not de Morgan. In another paper (the aptly named Conditions Related to de Morgan’s Law) Johnstone gives a slew of conditions equivalent to a topos being de Morgan. In particular, de Morgan-ness is equivalent to

1. $[\top,\bot] : 1+1 \to \Omega_{\lnot \lnot}$ being an isomorphism
2. $1+1$ being injective

But we can show both of these are false (thus giving two proofs that $\mathcal{T}$ is not de Morgan).

For $1$, we can compute that \(\mathcal{T}_{\lnot \lnot}\) is equivalent to $\mathsf{Set}$, where the equivalence sends a set $X$ the space $X$ equipped with the indiscrete topology. This is stated at the end of Section 3 of Johnstone’s original paper. In particular, $1+1$, which has the discrete topology, is not isomorphic to \(\Omega_{\lnot \lnot}\) (which is indiscrete).

For $2$, we know that in $\mathsf{Seq}$ there’s a map $(0,1) + (2,3) \to 1+1$ which doesn’t extend to a map $(0,3) \to 1+1$. Since monos in $\mathsf{Seq}$ are still monos in $\mathcal{T}$ (since the inclusion is a right adjoint), we’re done.

---

This was a long one! Multiple months in the making, and easily the most research I’ve ever done for a blog post (both in terms of reading done and original proofs). It was super rewarding, though, and I feel way better about the topological topos and its internal logic, as well as about topos theory more broadly ^_^.

Hopefully I was able to explain it clearly enough to be useful to all of you too! I know it’s a TON of information, and in the process of revising this I really struggled to tell if it’s well exposited or not since it kind of feels like this

But even though it’s a ton of information, hopefully each section is digestible!

Thanks again for reading all. I have other posts planned, about my thesis work for a change, but I think I’m going to take a break from writing after this, haha.

Stay safe, and talk soon! 💖

---

Appendix: A Proof that Johnstone’s Topos Models Brouwer’s Continuity Principle

If you’re not super familiar with externalizing formulas, you might want to read my old blog post with a bunch of simpler examples before trying to tackle this one!

We’ll be doing this computation using the site with one object \(\mathbb{N}_\infty\).

$\ulcorner$ We want to show that

\[\mathbb{N}_\infty \Vdash \ulcorner \text{every function $X \to Y$ is $\epsilon$-$\delta$ continuous} \urcorner\]

Cashing out the universal quantifiers, we want to show that for any continuous functions \(f : \mathbb{N}_\infty \times X \to Y\), \(\epsilon : \mathbb{N}_\infty \to \mathbb{R}_{\gt 0}\), and \(a : \mathbb{N}_\infty \to X\) in “the real world” we have

\[\mathbb{N}_\infty \Vdash \exists \delta : \mathbb{R}_{\gt 0} . \ \forall b : X . \ d(a,b) \lt \delta \to d(fa,fb) \lt \epsilon\]

To witness the existential quantifier, we need to find a cover of \(\mathbb{N}_\infty\), and produce a real-world $\delta$ defined on each member of the cover.

Finding a cover basically amounts to finding a cofinite subset of $\mathbb{N}$, and passing to a tail of all the sequences in sight. With this in mind, we choose a compact neighborhood $K$ of $a_\infty$ (using local compactness of $X$), and choose \(\delta^*\) so that \(B(a_\infty, \delta^*)\) is contained in $K$ and for every $x \in B(a_\infty, \delta^*)$ we have $d(f_\infty a_\infty, f_\infty x) \lt \frac{\epsilon_\infty}{6}$ (using continuity of $f_\infty$).

Then, let $N$ be large enough that for all $n \gt N$:

1. $\epsilon_n \gt \frac{\epsilon_\infty}{2}$
2. $d(f_n a_n, f_\infty a_\infty) \lt \frac{\epsilon_\infty}{6}$
3. For all $x \in K$, we have $d(f_\infty x, f_n x) \lt \frac{\epsilon_\infty}{6}$
4. $d(a_n, a_\infty) \lt \delta^*$

In condition (3) we’ve used the fact that $f_n$ converges to $f_\infty$ uniformly on the compact set $K$.

Now we take as our covering familiy

• the constant functions \(k : \mathbb{N}_\infty \to \mathbb{N}_\infty\)
• \(i_S : \mathbb{N}_\infty \to \mathbb{N}_\infty\) for any infinite subset \(S \subseteq \{ n \gt N \} \subseteq \mathbb{N}\).

As a reminder, the function $i_S$ is the unique monotone function \(\mathbb{N}_\infty \to \mathbb{N}_\infty\) whose image is \(S \cup \{\infty\}\).

Now on each member $g$ of this family, we need to produce a function \(\delta : \mathbb{N}_\infty \to \mathbb{R}_{\gt 0}\) which witnesses

\[\mathbb{N}_\infty \Vdash \forall b : X . \ d(a_{g(-)}, b) \lt \delta \to d(f_{g(-)}(a_{g(-)}), f_{g(-)}(b)) \lt \epsilon_{g(-)}\]

Cashing out the last universal quantifier, we need to know that for all \(h : \mathbb{N}_\infty \to \mathbb{N}_\infty\) and for all continuous \(b : \mathbb{N}_\infty \to X\),

If \(\mathbb{N}_\infty \Vdash d(a_{gh(-)},b) \lt \delta_{h(-)}\) then we must have \(\mathbb{N}_\infty \Vdash d(f_{gh(-)}(a_{gh(-)}), f_{gh(-)}(b)) \lt \epsilon_{gh(-)}.\)

So let’s build such a $\delta$ for the two cases in our cover!

First, if $g$ is the constant $k$ function. Then we need a convergent sequence $\delta_n$ so that for any function \(h : \mathbb{N}_\infty \to \mathbb{N}_\infty\) and any convergent sequence $b_n$ in $X$,

If $d(a_k,b_n) \lt \delta_{hn}$ for all $n$, then $d(f_k(a_k), f_k(b_n)) \lt \epsilon_k$ for all $n$ too.

Of course, this is easy to arrange by taking $\delta_n$ to be the constant sequence witnessing continuity of $f_k$ at $a_k$.

Second, if $g = i_S$ is the unique monotone function whose image is \(S \cup \{ \infty \}\). Recall also that every member of $S$ is at least $N$.

Then we define $\delta_n$ to be \(\delta^* - d(a_{i_S n}, a_\infty)\). Note this is convergent, with limit \(\delta^*\). Now we must show for any function \(h : \mathbb{N}_\infty \to \mathbb{N}_\infty\) and for any convergent sequence \(b_n\) in $X$ that

If $d(a_{i_S h n}, b_n) \lt \delta_{hn}$ for all $n$, then $d(f_{i_S h n}(a_{i_S h n}), f_{i_S h n}(b_n)) \lt \epsilon_{i_S h n}$.

But since $i_S h n \gt N$ and \(d(b_n, a_\infty) \leq d(b_n, a_{i_S h n}) + d(a_{i_S h n}, a_\infty) \lt \delta^*\) we see that

1. $\epsilon_{i_S h n} \gt \frac{\epsilon_\infty}{2}$
2. $d(f_{i_S h n}(a_{i_S h n}), f_{\infty}(a_\infty)) \lt \frac{\epsilon_\infty}{6}$
3. $d(f_\infty b_n, f_{i_S h n} b_n) \lt \frac{\epsilon_\infty}{6}$

so that we can compute

\[\begin{aligned} d(f_{i_S h n}(a_{i_S h n}), f_{i_S h n}(b(n))) &\leq d(f_{i_S h n}(a_{i_S h n}), f_\infty(a_\infty)) + d(f_\infty(a_\infty), f_\infty(b_n)) + d(f_\infty(b_n), f_{i_S h n}(b_n)) \\ &\leq \frac{\epsilon_\infty}{6} + \frac{\epsilon_\infty}{6} + \frac{\epsilon_\infty}{6} \\ &= \frac{\epsilon_\infty}{2} \\ &\lt \epsilon_{i_S h n} \end{aligned}\]

As desired. $\lrcorner$

---