Why Care About Infinity Categories? (Homotopy Theories pt 2/4)
11 Jul 2022 - Tags: homotopy-theories
The title of this post is slightly misleading. It will be almost entirely
about
With the intro out of the way, let’s have a quick recap.
The setting we’re interested in is a category
We want to build a new category
(called the homotopy category or localization)
A model structure on a pair
A model structure on
Unfortunately, as we noted at the end of the last post, model categories are not without flaws. As soon as we want to talk about relationships between model categories, we start running into trouble. For instance, there’s no good notion of a functor between model categories.
What, then, are we to do? The answer is to fully accept homotopy theory as part of our life, and to move to a notion of “category” which is better equipped to handle the geometry which is implicit in the machinery of model categories.
To start, we need a model of “spaces” that’s more convenient to work with than topological spaces.
A Simplicial Set is a functor
Here
Every object in
which we call
We should think of
Now, to every topological space
It turns out that
But there’s a natural follow up question: Can we recognize when a
simplicial set is
For now we’ll content ourselves with the knowledge that
simplicial sets, up to homotopy equivalence, represent spaces
in a convenient way. For those following along, this is the
Quillen equivalence between
We’ll write
A Simplicial Category is a category
enriched in
That is, given two objects
There is a natural notion of equivalence between two simplicial categories,
called Dwyer-Kan equivalence, then we (tentatively) say an
Given an
As an example, we might have two arrows
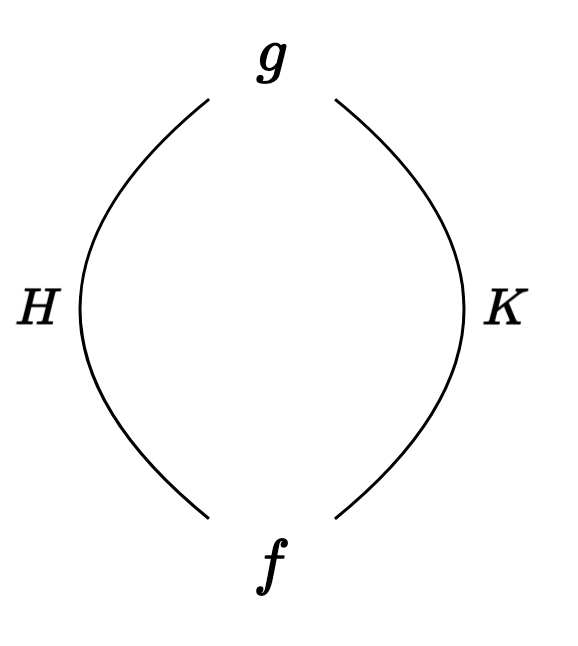
When we take connected components, these two maps
We’ll see another, more realistic example, once we know how to build an
So how do we build an
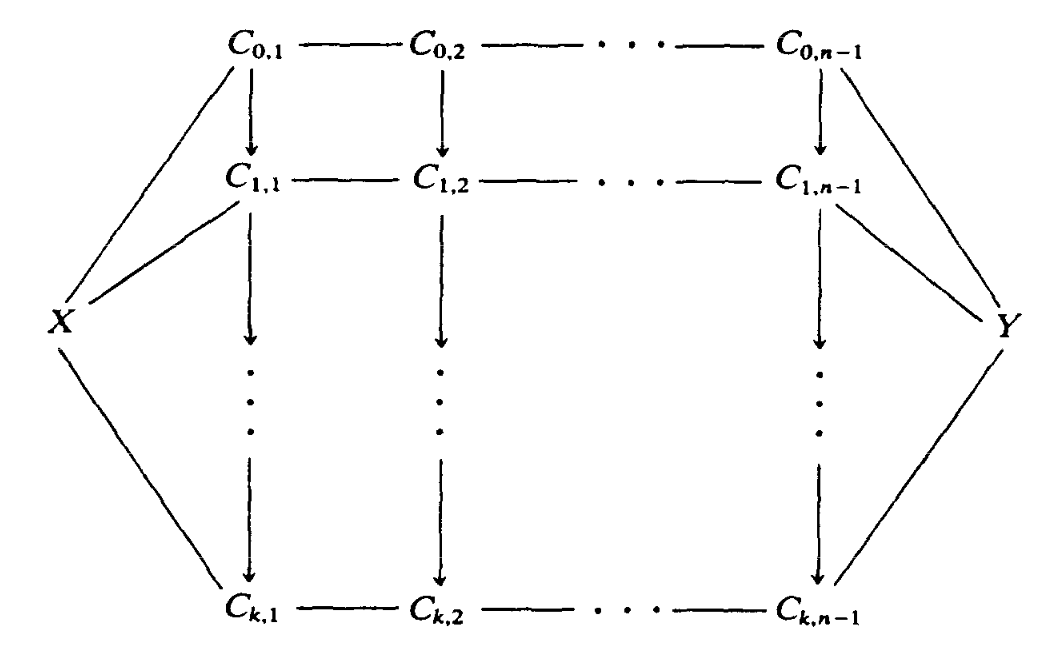
We want to build up a space of maps
The
-
-
-
-
- etc.4
where the left-pointing arrows are weak equivalences. Notice that, after we
invert the weak equivalences, the left facing arrows will have inverses,
which will compose with the other right facing arrows to give an
honest-to-goodness arrow
Now, a
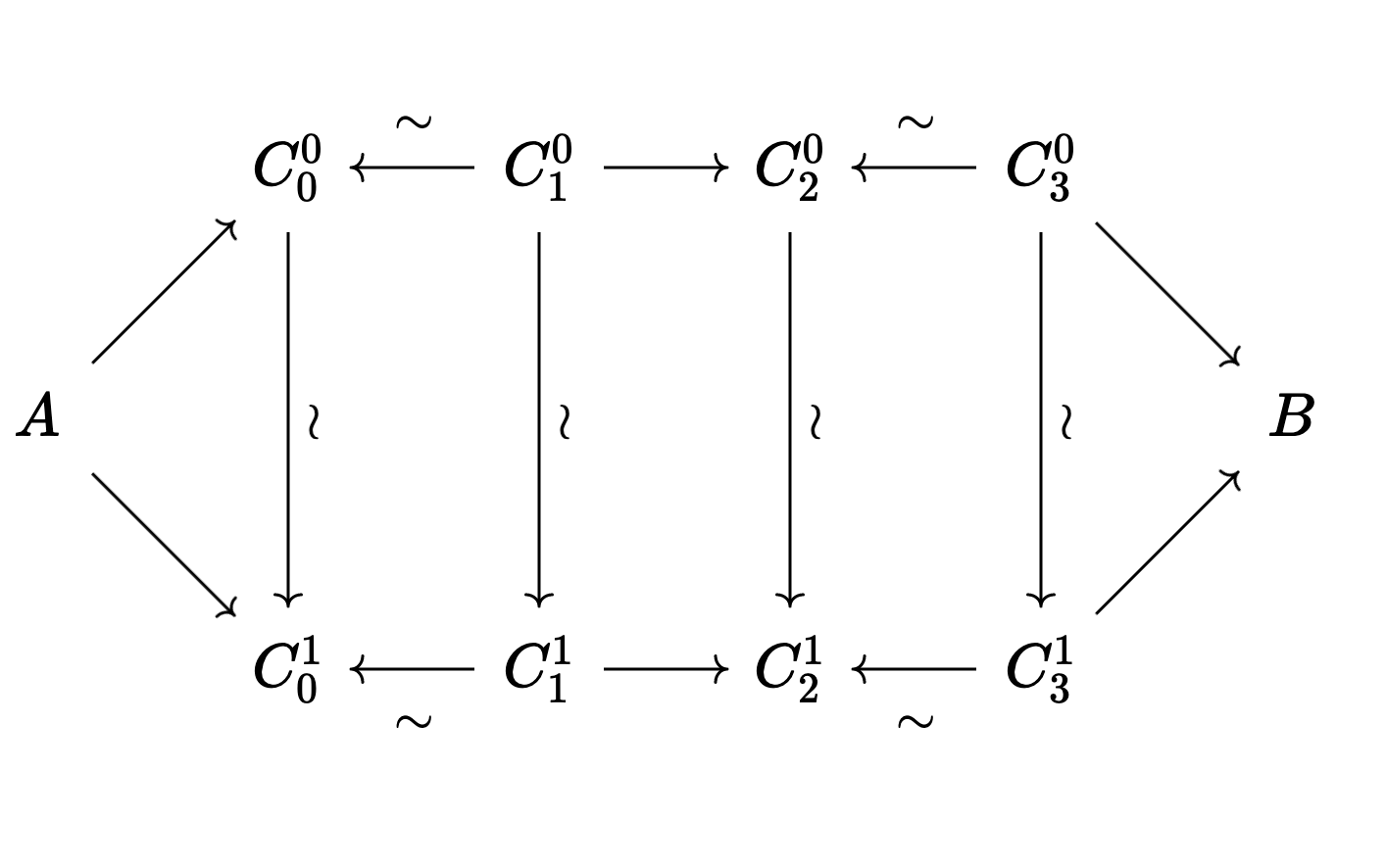
Similarly, a
As before, the vertical arrows should all be weak equivalences, as should all the backwards facing arrows in the zigzags.
Of course, we need the face maps between simplicies. We get the
The resulting
Notice that the homotopy category of

Let’s see an example. Consider the category
where
Say we want to invert
Let’s compute
It should have a
For
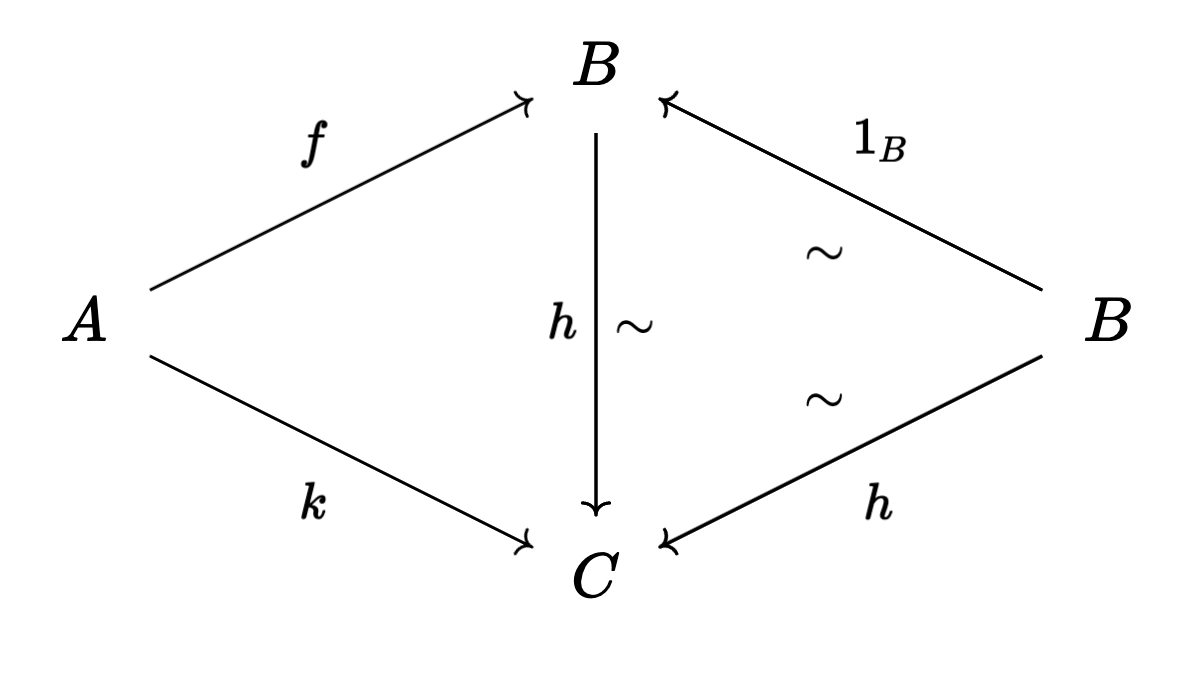
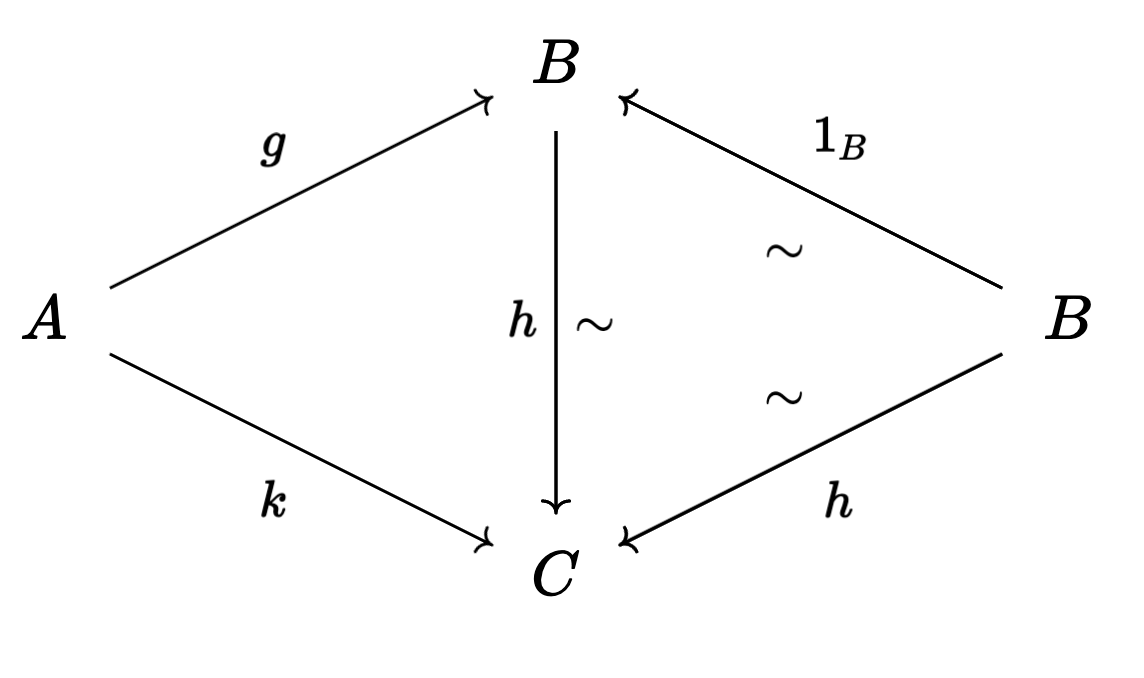
So that
which is, of course, contractible. Crucially, though, this space is
capable of remembering more information about how the maps
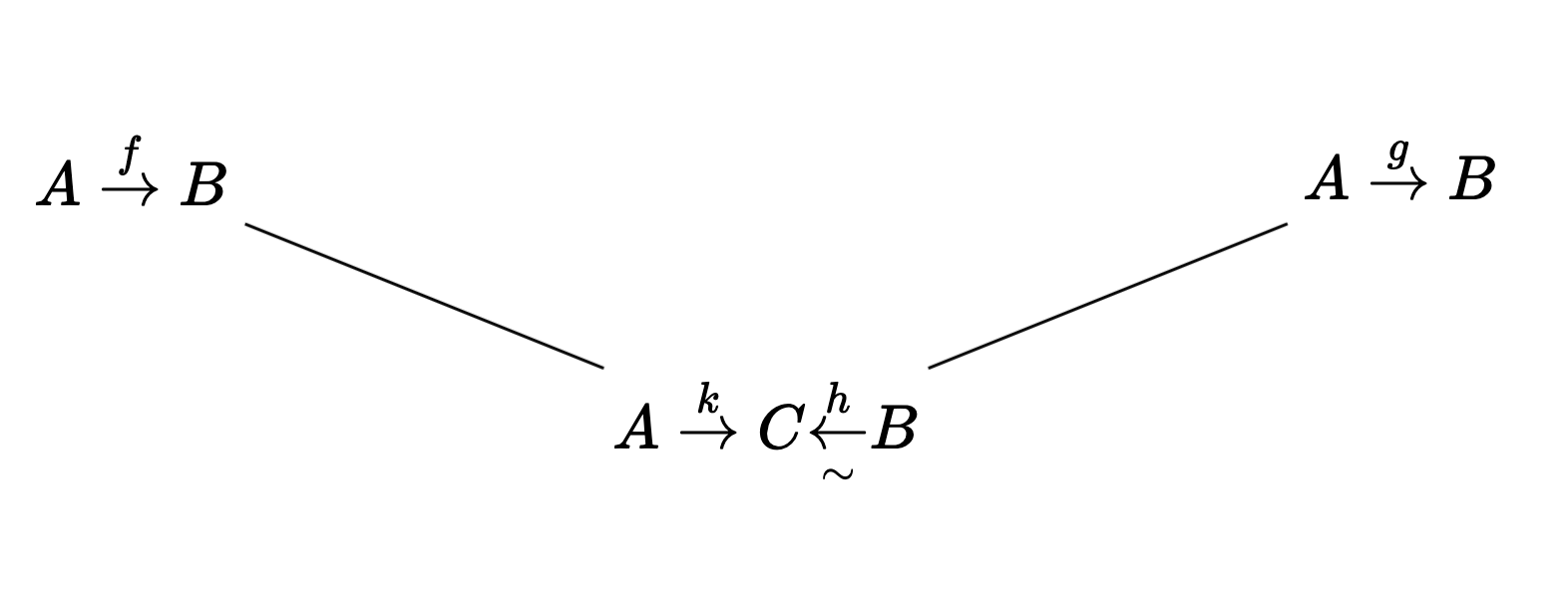
Consider instead the category
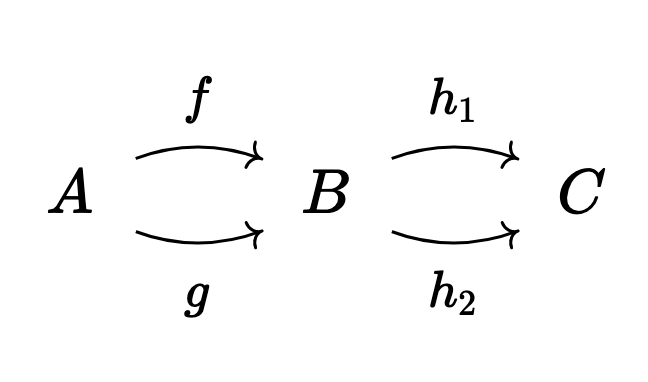
where
Show that, after inverting
This is great, but it’s far from clear how we would do this for more
complicated categories! This is ok, though. Remember that
It begs the question, though: just how nice are
Let’s start with the most obvious issue with model categories: the lack of
functors between them. Once we pass to
If
Importantly, we have exactly one notion of functor between model categories,
namely the quillen equivalences. We would like to know that these are
faithfully preserved when we pass to
Next, not only do we have a notion of functor, but we have a notion of
functor which acts the way we expect it to. For instance between any
From here, developing (co)limits is easy!
If
We say that a cone on
is an equivalence of simplicial sets7.
If this looks like an adjunction between a “limit” functor and
the “const” functor, then you’d be right! We can actually develop
adjunctions in this theory as well, and indeed basically any construction
or theorem you would want to use from classical
So, miraculously, in the passage from model categories to
What’s even more remarkable is that this notion of a (co)limit computes homotopy (co)limits as a special case!
In the next post about quasicategories, we introduce the
nerve construction, which lets us build an
Lastly, let’s note that this is all good for something.
Functors on
This still leaves open some questions, though. First, it seems like there are
two competing notions of
Moreover, while the hammock localization is nice, it seems really annoying to work with. Can we play the game one more time, and end up with a conceptually clean way to see what the hammock localization is “really doing”?
For answers to both of these questions, I’ll see you in the
last post of this trilogy… tetralogy?
Maybe it’s best to call it a trilogy with a long quasi-categorical ~bonus post~.
Take care, all ^_^
-
Think about
-
Notice this is exactly what we do to make (co)homological computations with simplicial chains in topology. ↩
-
You can read more in the (surprisingly readable!) paper Calculating Simplicial Localizations by Dwyer and Kan.
Another approach to simplicial localization is explained in another readable paper by the same authors: Simplicial Localizations of Categories. It’s a perfectly good definition, and works well in the abstract, but the “hammock” definition is more amenable to direct computation, since it’s slightly more explicit.
-
It’s actually slightly more general. The first arrow is also allowed to point left, as long as things still alternate. For instance, we allow a zigzag of the form
as well.
For the specifics of the construction, see Calculating Simplicial Localizations by Dwyer and Kan. ↩
-
As before, we also allow the first map to face left instead of right, as long as our maps strictly alternate. What does this mean for our hammocks? The horizontal threads of our hammock must be oriented the same way!
For instance, this is a valid hammock:
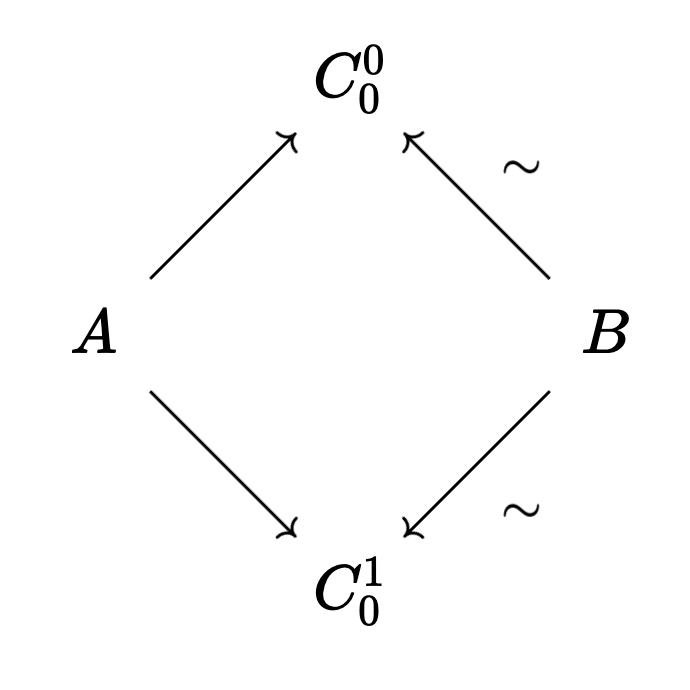
This is a valid hammock:
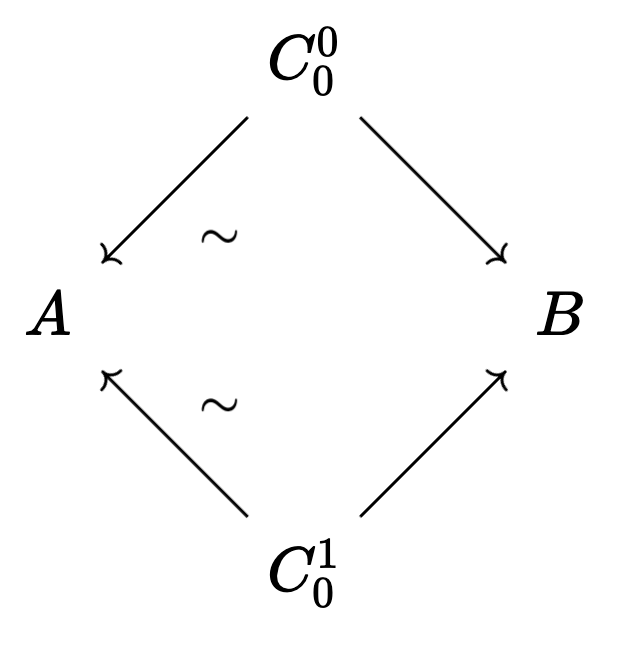
But this is not a valid hammock:
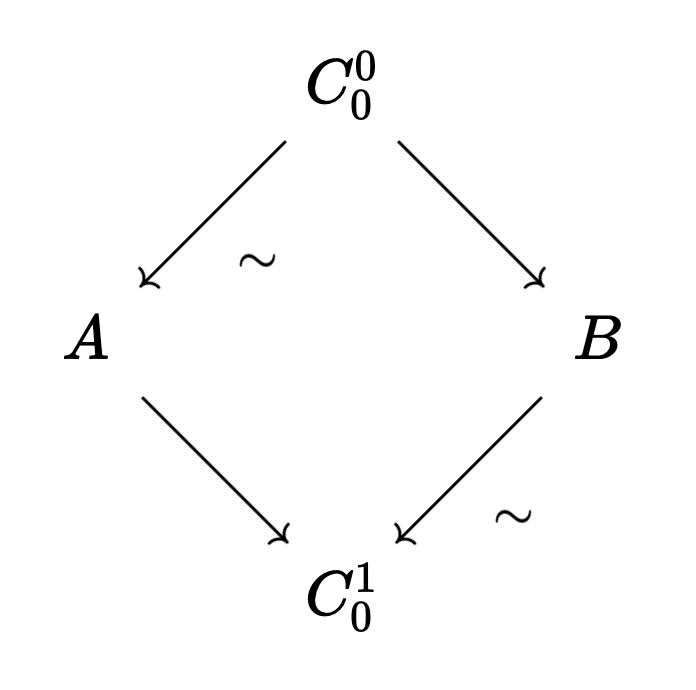
Also, I can’t express enough how much I love this naming idea! It’s quirky and apt in equal measure. 10/10. ↩
-
We can actually get by with slightly less.
-
If you want to learn about actually computing with
The second video already shows lots of sample computations for limits. ↩