An Interlude -- Quasicategories (Homotopy Theories pt 3/4)
11 Jul 2022 - Tags: homotopy-theories
In the previous post, we defined
First, then, a reminder:
A Simplicial Set is a (contravariant)
functor from the simplex category to
This seems strange at first, but it turns out that we can model many different kinds of behavior using simplicial sets.
Most notably, simplicial sets are a common generalization of both topological spaces (up to homotopy) and categories!
We’ve already seen how simplicial sets can represent topological spaces up to
homotopy (this is given by a quillen equivalence of model structures on
We know that
I mentioned earlier that simplicial sets can directly generalize categories…
Maybe there’s some way to define
The answer will be “yes”, but let’s start small. Is there a way for us to
recognize when a simplicial set is
The
For instance, let’s look at
Concretely,
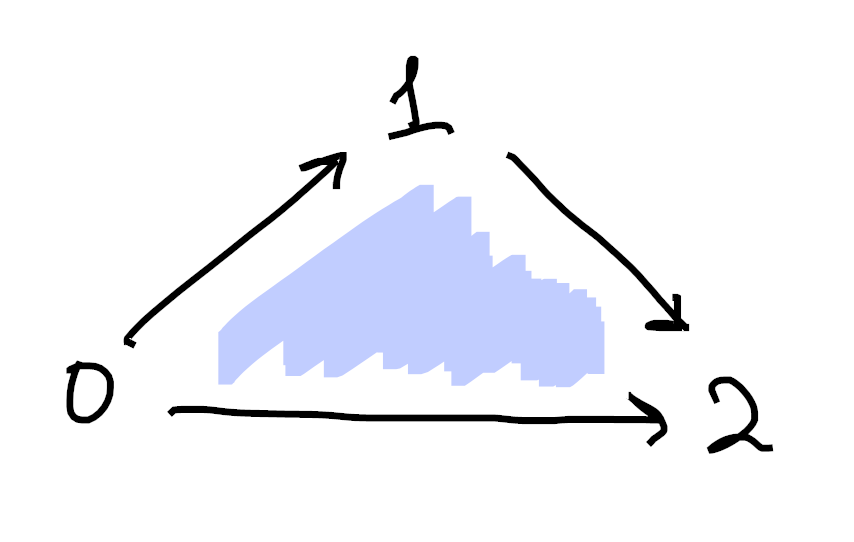
Then the
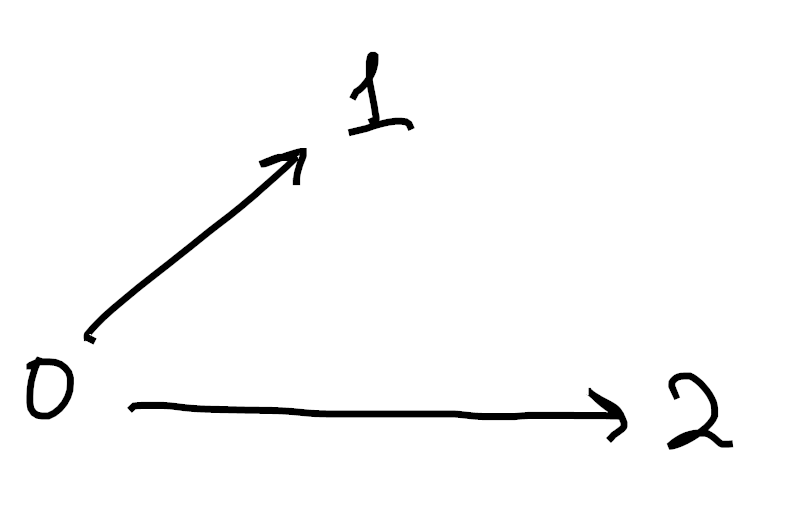
Analogously, we get
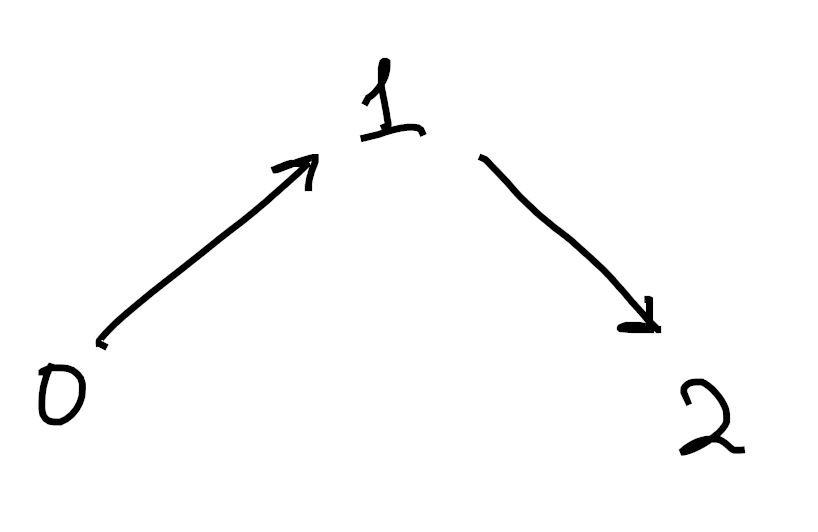
and we get
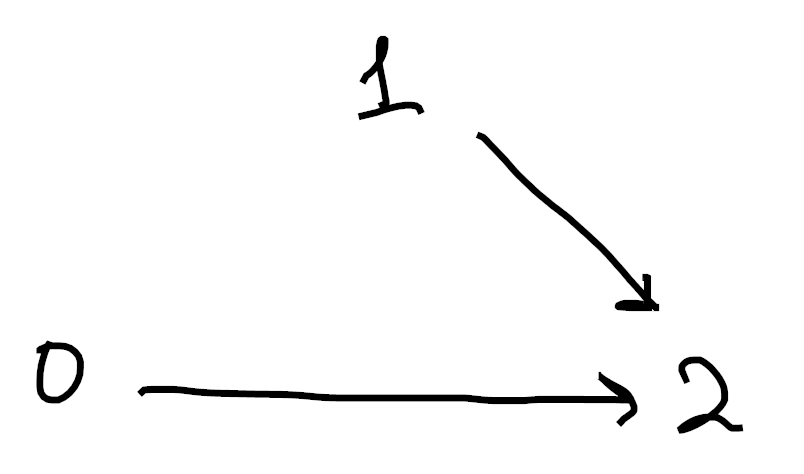
What about the horns of
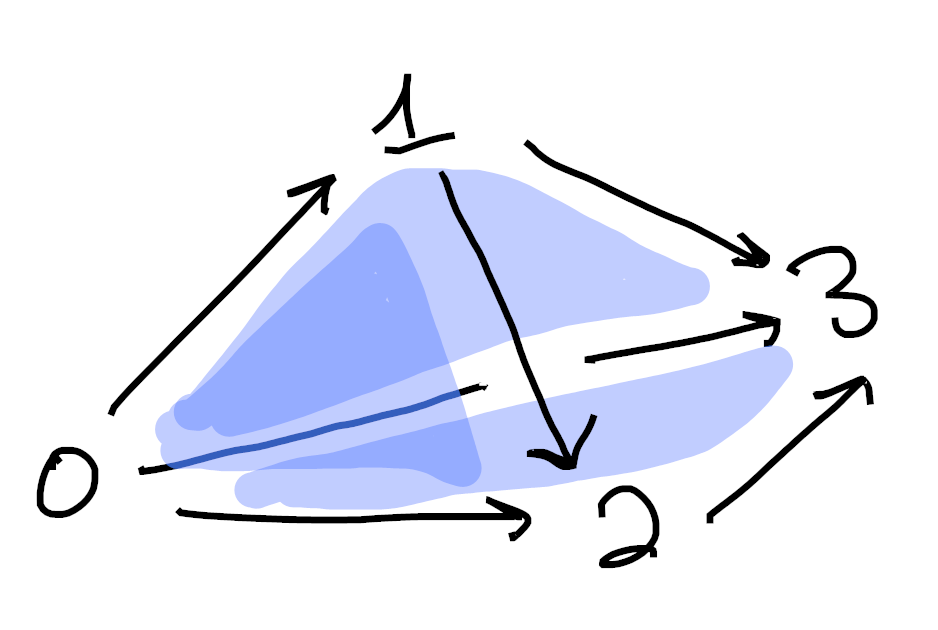
Similarly,
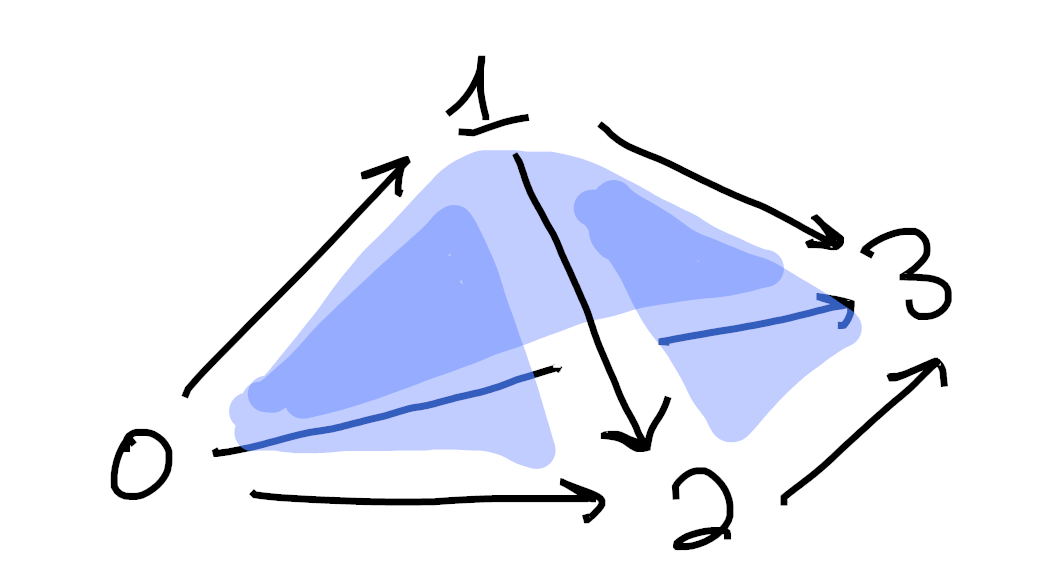
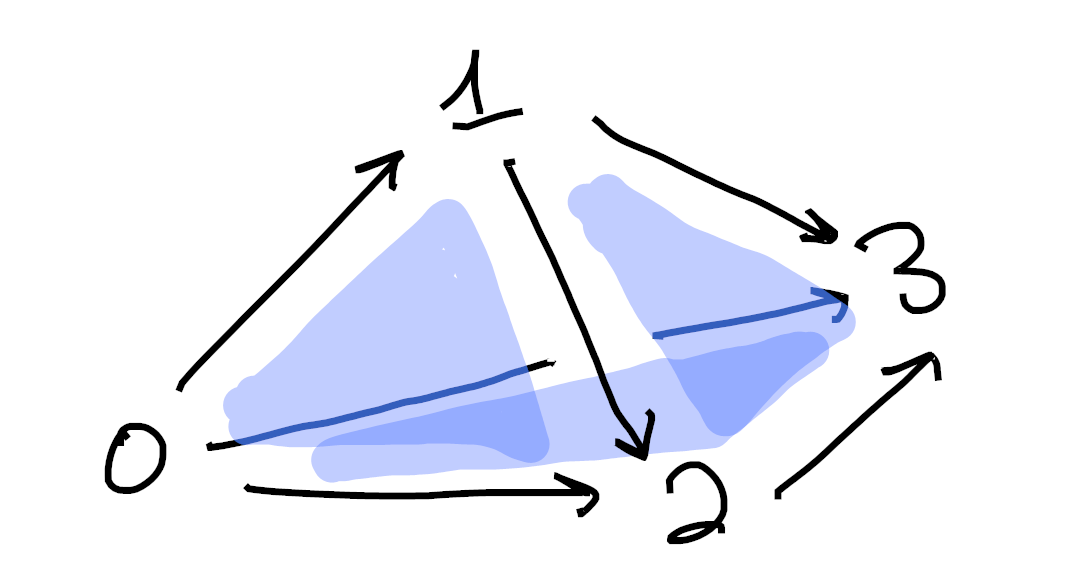
and
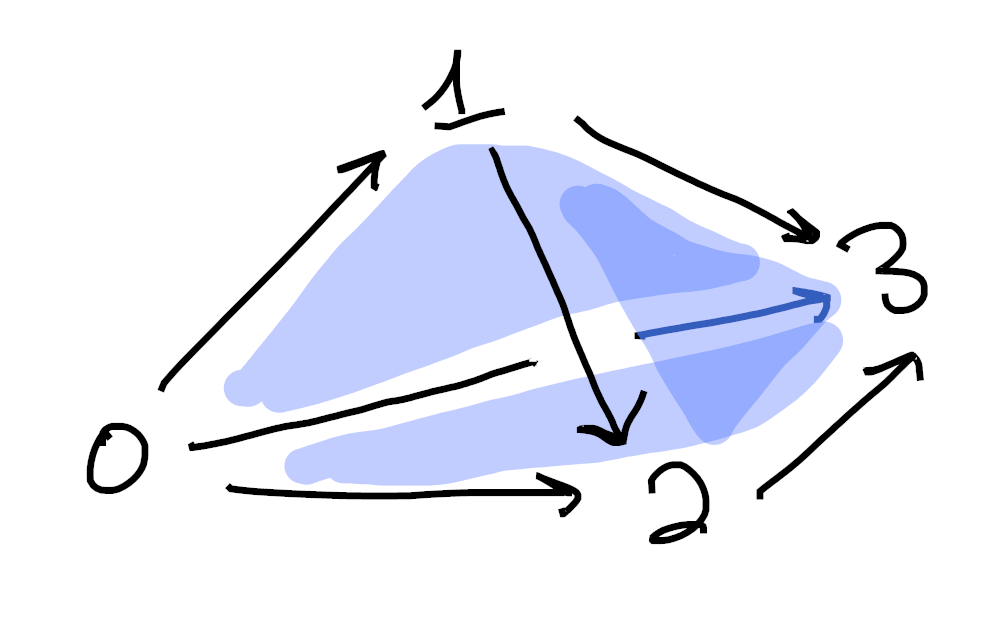
As a (quick?) exercise, you should try to write down a definition of
Remember that, by the yoneda lemma, it (more or less) suffices to say what the
Now then, we come to an important definition
A simplicial set
In a commutative diagram, we ask that the following dotted morphism should always exist:
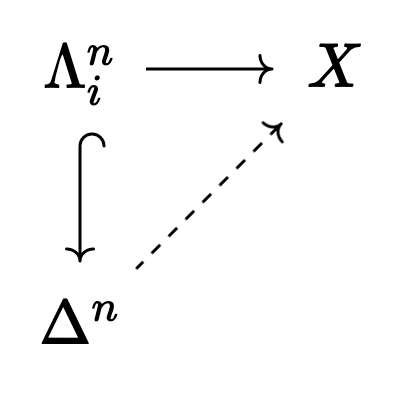
Why care about this? Because of the following major theorem:
For every topological space
Moreover, (up to weak equivalence), every kan complex arises in this way.
So we see that we can completely recover the notion of topological space (up to homotopy) by looking at special simplicial sets… But wasn’t this all supposed to have something to do with category theory?
Just like every topological space
In general, the
- The 0-cells will be objects of
- The 1-cells will be the arrows,
- The 2-cells will be the paths of length 2,
- The 3-cells will be the paths of length 3,
- etc.
Concretely, let’s look at the following category (where
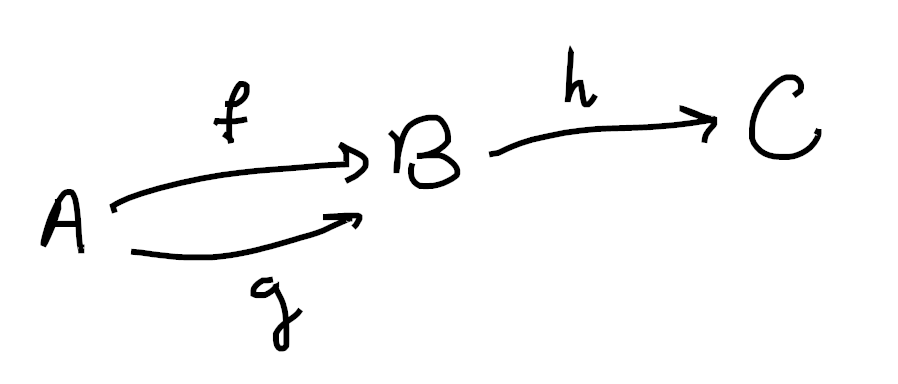
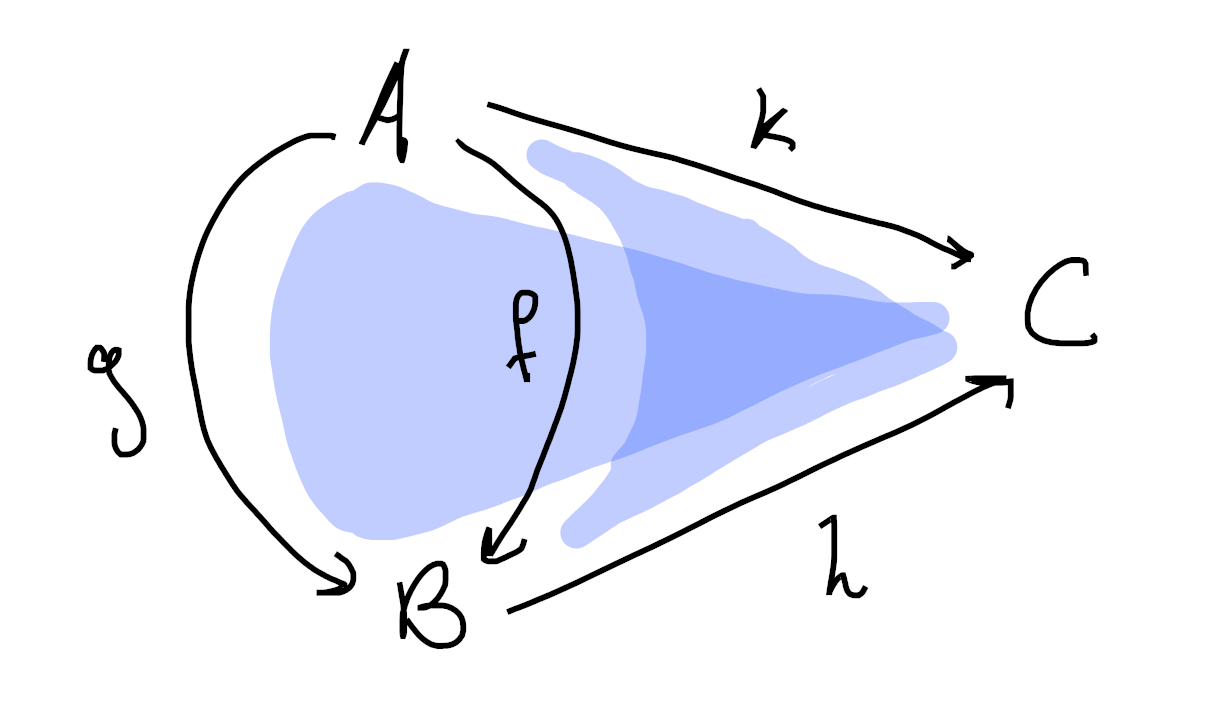
Then its nerve should have three 0-cells (
since
Thus, the nerve of
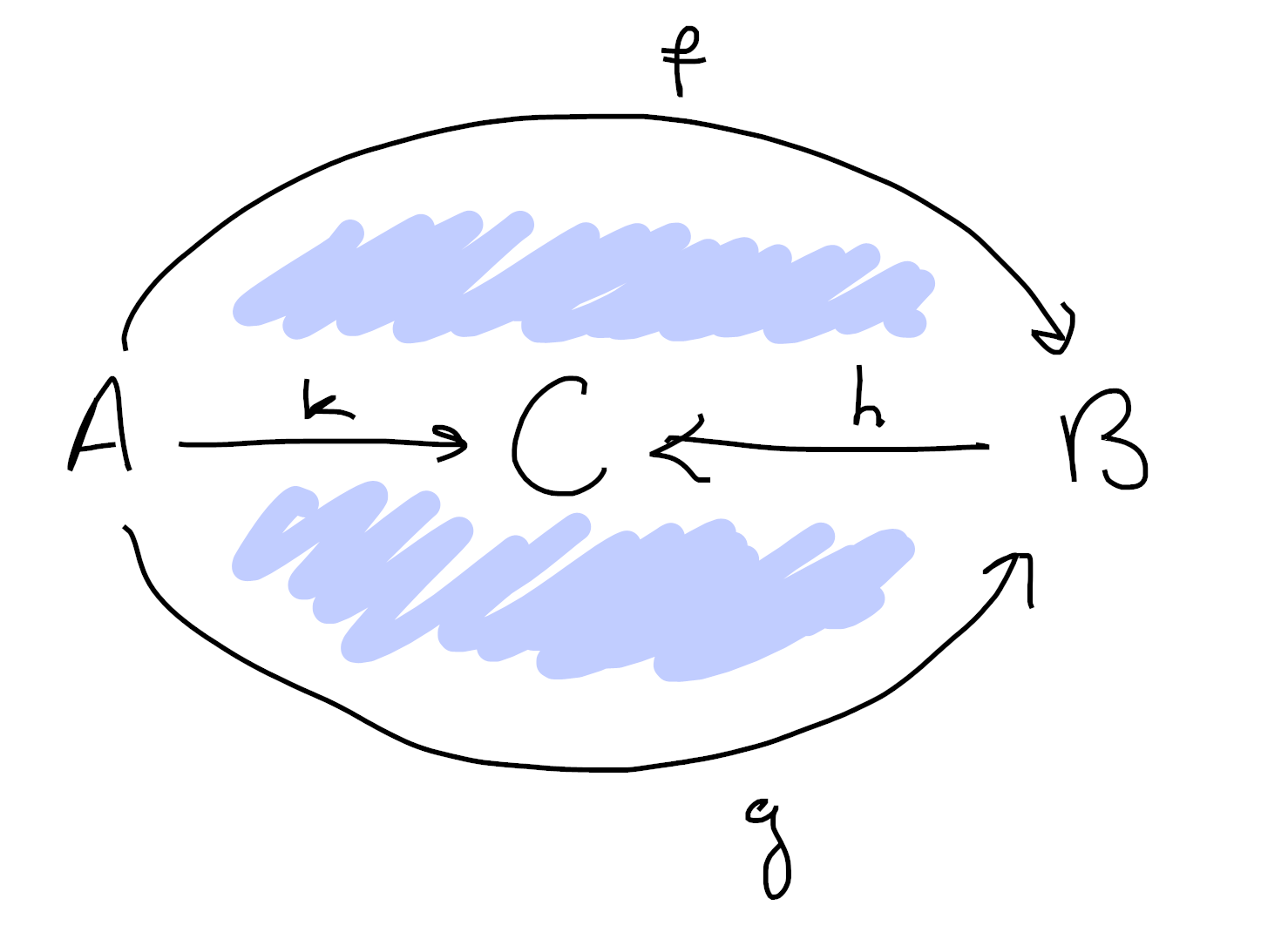
Perhaps a better way to visualize this is as a disk instead:
Of course, it’s easy to guess the next question. Can we tell which simplicial complexes arise as the nerve of some category?
Again, the answer is yes, and the answer will look shockingly similar to the case of topological spaces!
A simplicial complex is called a Quasicategory if every “inner horn” has a fill.
That is, every horn
This should make sense as a definition, since in a category composition tells us that we can fill inner horns!
Indeed, consider the inner horn
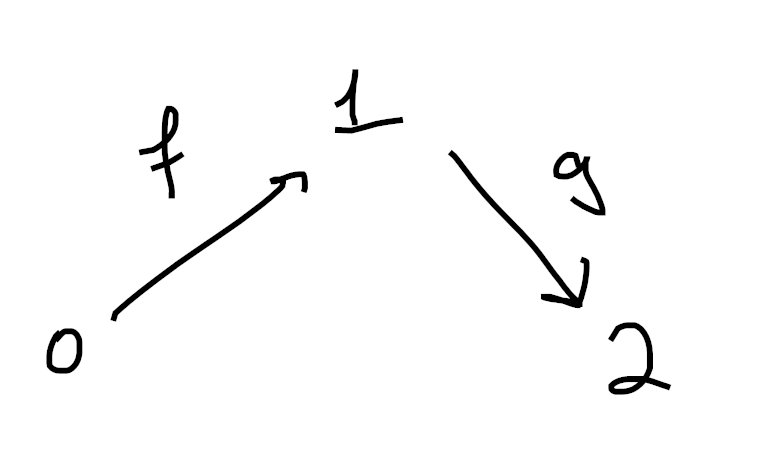
If this diagram lives inside the nerve of a category
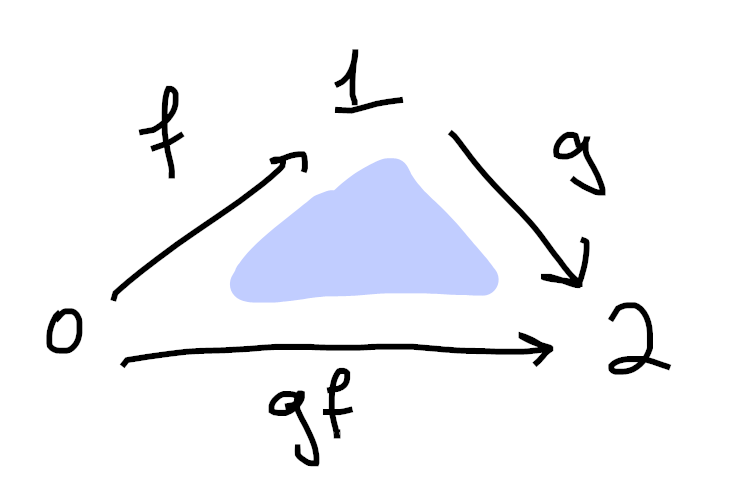
As a cute exercise, you should check that the two inner horns
This all brings us to another major theorem:
For every category, the nerve
Moreover, if
Moreover again, the nerve construction embeds the category of categories fully and faithfully into the category of quasicategories.
Importantly, this means that every kan complex is a quasicategory! This tells us that quasicategories allow us to treat spaces and categories on equal footing4!
In particular, quasicategories give us a setting where we can
“do homotopy theory” to categories, and if you remember back to
the main post about
Here’s another tentative definition. If this reminds you of the tentative definition of a “homotopy theory” from the last post, you have good instincts.
An
This is great because it gives us a super concrete way of working with
In this framework, our categories literally are geometric objects! The category of simplicial sets is a topos, so it has as many nice constructions as we could want, and many of these preserve kan complexes and quasicategories.
For instance, now functors are just simplicial maps, many limits and colimits of quasicategories can be computed as with geometric objects, exponentials give us functor quasicategories, and all of these work as well as we could hope.
Because of this concreteness,
Jacob Lurie’s tomes on
How can we reconcile these viewpoints? Is there a way for us to apply
the machinery proven in Lurie’s books to the hammock localization of
a model category? Is there some way for us to
use these nice geometric definitions for computations involving quasicategories,
and leverage them to understand the simplicial categories we’ve been talking
about? Why have we given two seemingly unrelated definitions of an
For answers to these questions and more, read on to the last post in this series5!
-
Super concretely, given
the
- the unique
- the unique
- the unique
-
Sorry if these are hard to understand. Drawing 3d pictures is hard, haha. Each image is made up of 1-cells (colored in black) as well as 2-cells (shaded in blue). Moreover, in each picture we’ve omitted exactly one 2-cell from the boundary of the tetrahedron. ↩
-
If it’s not clear what role yoneda plays in this situation, see my answer here.
It’s also definitely worth reading Friedman’s An Elementary Illustrated Introduction to Simplicial Sets (avaialable here). ↩
-
I originally put this in the main body, but I ended up deciding it ruined the flow of the post too much. That said, I still think it’s a fun (and enlightening) example, so I wanted to include it as a ~bonus exercise~ here:
Show that two isomorphic categories give rise to homeomorphic nerves (after taking geometric realizations, of course).
Then, show that two equivalent categories give rise to homotopy equivalent nerves.
-
Thank goodness! I have been working on these for so long. I really didn’t realize how big a project I was in for when I decided to make a post clarifying the relationship between model categories and
I love how it’s turning out, but I’m so ready for these posts to be behind me, haha. I also didn’t want to post any of them until they were all done. In part because I spent a lot of time moving various bits back and forth between posts, and once one is public I would want to consider it (mostly) set in stone. But also because I wanted to make sure I actually finished them all.
I have a bad habit of starting a series and leaving things unfinished (rest in peace cohomology part 1), but it was important that I not do that to these posts. ↩